人教版数学七年级下册 第8章 8.3实际问题与二元一次方程组同步测试试题(一)(Word版含解析)
文档属性
| 名称 | 人教版数学七年级下册 第8章 8.3实际问题与二元一次方程组同步测试试题(一)(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 21:40:40 | ||
图片预览




文档简介
实际问题与二元一次方程组同步测试试题(一)
一.选择题
1.足球比赛中,每场比赛都要分出胜负每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )
A. B.
C. D.
2.小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会差25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则( )
A.他身上的钱会不足95元
B.他身上的钱会剩下95元
C.他身上的钱会不足105元
D.他身上的钱会剩下105元
3.七年级某班由于布置班级的需要,用彩纸剪出了一些“星星”和”花朵”.一张彩纸可以剪出6个“星星”或4个“花朵”,已知剪出的“星星“数量是“花朵”数量的3倍,该班级共用了10张彩纸,设用x张剪“星星”,y张剪“花朵”,根据题意,可列方程组为( )
A. B.
C. D.
4.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )
A. B.
C. D.
5.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
6.为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )
A. B.
C. D.
7.《九章算术》中有一道“盈不足术”问题,原文为:今有人共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:现有几个人共同购买一件物品,每人出8钱,则多3钱;每人出7钱,则差4钱,求物品的价格和共同购买该物品的人数.设该物品的价格是x钱,共同购买该物品的有y人,则根据题意,列出的方程组是( )
A. B.
C. D.
8.如图,将正方形ABCD的一角折叠,折痕为AE,点B恰好落在点B'处,∠B′AD比∠BAE大48°.设∠BAE和∠B′AD的度数分别为x°和y°,那么所适合的一个方程组是( )
A. B.
C. D.
9.栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?歌谣大意是:一群乌鸦落在一片树上,如果三个乌鸦落在一棵树上,那么就有五个乌鸦没有树可落;如果五个乌鸦落在一棵树上,那么就有一棵树没有落乌鸦,请问乌鸦和树各多少?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B.
C. D.
10.《孙子算经》是我国古代数学名著之一,里面有一个“二人持钱的问题,其题意是有甲、乙两人所带钱数量不详,甲若得到乙所带钱数的一半,甲的钱数就达到48,乙若得到甲所带钱数的,乙的钱数也将达到48,问甲、乙两人原来各带多少钱?若设甲、乙两人原来各带的钱数分则是x和y,小明和小伟所列方程细分别是:小明:小伟:则关于所列方程组,下列说法正确的是( )
A.小明对,小伟不对 B.小明不对,小伟对
C.两人都不对 D.两人都对
二.填空题
11.若k个连续正整数之和为2010,则k的最大值是 .
12.学生问老师:“您今年多大了”老师风趣地说:“我像你这么大时,你刚1岁;你到我这么大时,我已37岁了”.那么老师现在的年龄是 岁.
13.如图,把一个长21cm、宽15cm的长方形分成五块,其中两个大正方形和两个长方形形状和大小完全相同,那么中间小正方形的面积是 cm2.
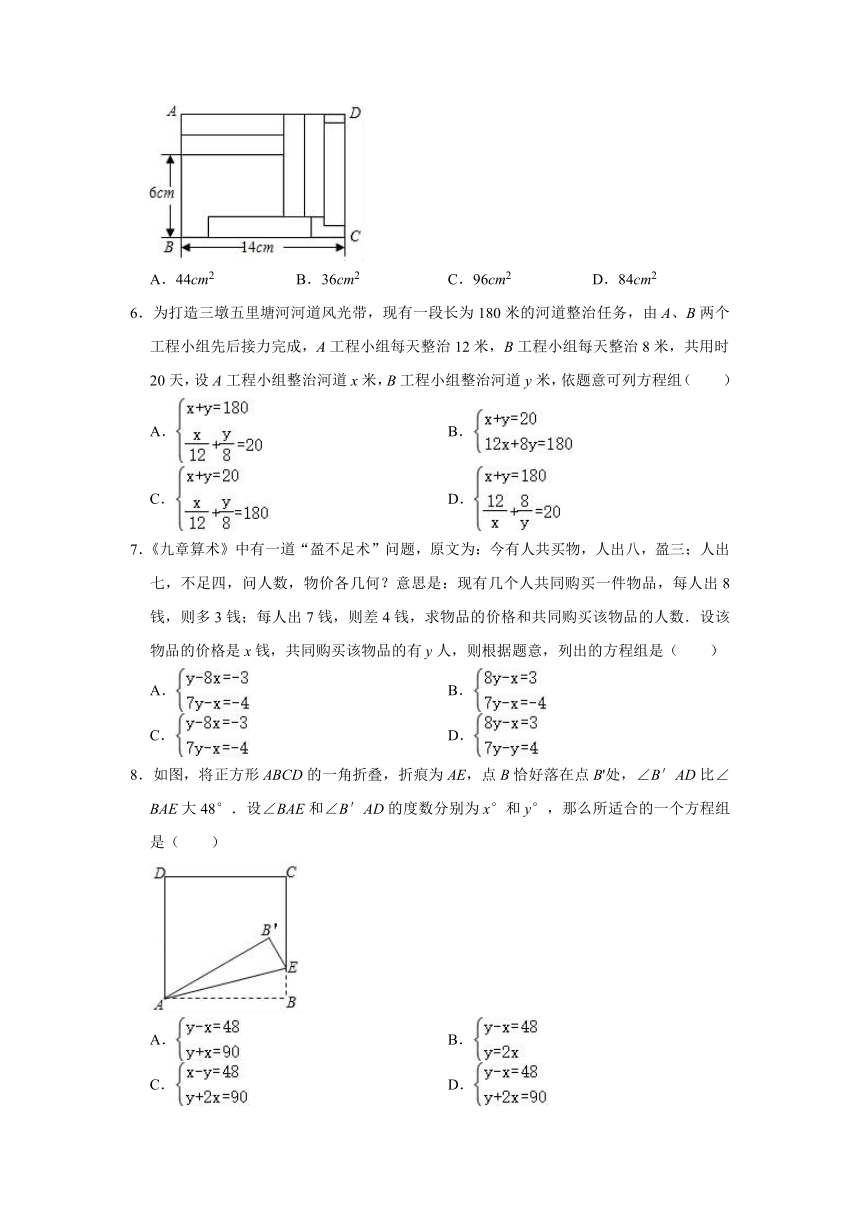
14.如图,在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,AB=14cm,AE=6cm,则图中阴影部分的总面积是 .
15.小颖家离学校1200米,其中有一段为上坡路,另一段为下坡路.她去学校共用了16分钟,已知小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时,去时上坡路和下坡路分别是多少千米?设去时上坡路x千米,下坡路y千米,则可列方程组: .
三.解答题
16.现有36卷相同的布料做工作服,每卷布料可制作成上衣25件,或者制作成裤子40件,一件上衣和两件裤子组成一套,问,用多少卷布料制作上衣,多少卷布料制作裤子可以使上衣和裤子正好配套?
17.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒,现有正方形纸板300张,长方形纸板700张,若这些纸板恰好用完,则可做横式、竖式两种纸盒各多少个?
18.今年学校举行足球联赛,在第一阶段的比赛中,每队都进行了8场比赛,小虎足球队胜了4场,平2场,负2场,得14分;小豹足球队胜了6场,平1场,负1场,得19分.已知,记分规则中,负1场得0分.
(1)求胜1场、平1场各得多少分?
(2)足球联赛结束后,小狮足球队共参加了17场比赛,得了24分,且踢平场数是所胜场数的正整数倍,请你想一想,小狮足球队所负场数有 种可能性.
19.某电器经营业主计划购进一批同种型号的空调和电风扇,若购进8台空调和20台电风扇,需要资金23600元;若购进10台空调和30台电风扇,需要资金31000元.
(1)空调和电风扇每台的采购价各是多少元?
(2)由于国家大力推行家电下乡政策,每台空调可以比采购价下调15%,每台电风扇可以比采购价打七折.该业主计划用29930元购进两种电器共20台,其中空调不少于13台,该业主能否实现购买计划?如能实现,请帮他列出购买计划;如不能,请说明理由.
(3)该业主计划增加购买单价为每台600元的空调扇,且三种电器的总数量共50台,空调扇总数10至20台之间(不包含10、20),恰好投入55000元.若最终实际利润为,每台空调300元,每台电扇30元,每台空调扇100元.该业主决定将本次购买计划的全部利润对口捐给某医院,助益抵抗新冠肺炎疫情,现医院有7500元资金缺口.该业主能否实现目标?如果能,请直接写出进货方案和获得的利润总额.
参考答案与试题解析
一.选择题
1.【解答】解:设这个队胜x场,负y场,
根据题意,得.
故选:A.
2.【解答】解:设签字笔的单价为x元,笔记本的单价为y元,
根据题意得:20x+15y﹣25=19x+13y+15,
整理得:x+2y=40,
∵小江购买17支签字笔和9本笔记本的钱为17x+9y,
∴19x+13y+15﹣(17x+9y)
=2x+4y+15
=2(x+2y)+15
=2×40+15
=95,
即小江身上的钱会剩下95元;
故选:B.
3.【解答】解:设用x张剪“星星”,y张剪“花朵”,根据题意,可列方程组为.
故选:A.
4.【解答】解:由题意可得,
,
故选:A.
5.【解答】解:设小长方形的长为xcm,宽为ycm,
依题意,得:,
解得:,
∴14×(6+2×2)﹣6×8×2=44(cm2).
故选:A.
6.【解答】解:设A工程小组整治河道x米,B工程小组整治河道y米,依题意可得:
,
故选:A.
7.【解答】解:设该物品的价格是x钱,共同购买该物品的有y人,
依题意,得:.
故选:B.
8.【解答】解:设∠BAE和∠B′AD的度数分别为x°和y°,
根据题意可得:.
故选:D.
9.【解答】解:设诗句中谈到的鸦为x只,树为y棵,则可列出方程组为:
.
故选:D.
10.【解答】解:设甲、乙两人原来各带的钱数分则是x和y,
根据题意,得:
所以小伟的正确,小明的错误.
故选:B.
二.填空题(共5小题)
11.【解答】解:设第一个正整数是a,则第k个正整数是a+k﹣1.
根据题意,得
a+a+1+…+a+k﹣1=2010,
=2010,
k2+(2a﹣1)k=4020,
k2+(2a﹣1)k﹣4020=0,
(k+)2=4020+,
因为a,k都是正整数,要求k的最大值,则a越小越好,则﹣4020=﹣60×67,
即此时a的最小值是4,k的最大值是60.
12.【解答】解;设老师现在x岁,学生现在y岁,则
解得
答:老师现在25岁.
故填25.
13.【解答】解:设大正方形的边长为xcm,设小正方形的边长为ycm,根据题意得:
,
解得:,
故小正方形的面积=3×3=9(cm2).
故答案为:9.
14.【解答】解:设小长方形的长为xcm,宽为ycm,
依题意得:,
解得:,
∴图中阴影部分的总面积=14×(6+2y)﹣6xy=14×(6+2×2)﹣6×8×2=44(cm2).
故答案为:44cm2.
15.【解答】解:可根据所用时间和所走的路程和得到相应的方程组为:,
故答案为:.
三.解答题(共4小题)
16.【解答】解:设用x卷布料制作上衣,y卷布料制作裤子可以使上衣和裤子正好配套,
依题意,得:,
解得:.
答:用16卷布料制作上衣,20卷布料制作裤子可以使上衣和裤子正好配套.
17.【解答】解:设可做横式纸盒x个,可做竖式纸盒y个,依题意有
,
解得.
故可做横式纸盒100个,可做竖式纸盒100个.
18.【解答】解:(1)设胜1场得x分,平1场得y分,
由题意得,
解得.
答:胜1场得3分,平1场得1分;
(2)设小狮足球队胜m场,平n场,负t场,
依题意得:,
∴n=24﹣3m,t=2m﹣7.
∵n是m的正整数倍,t≥0及m为整数,
∴m=4,n=12或m=6,n=6.
∴小狮足球队所负场数有 2种可能性.
故答案为:2.
19.【解答】解:(1)设空调每台的采购价是x元,电风扇每台的采购价是y元,
根据题意得:,
解得:.
答:空调每台的采购价是2200元,电风扇每台的采购价是300元;
(2)由题意得,每台空调的采购价为2200×(1﹣15%)=1870(元),每台电风扇的采购价为300×0.7=210(元).
设该业主购买空调a台,则购买电风扇(20﹣a)台,
根据题意得:,
解得:13≤a≤15.5,
∵a是整数,
∴a=13,14,15.
故该业主能实现购买计划,购买计划有三种:
①购买空调13台,电风扇7台;
②购买空调14台,电风扇6台;
③购买空调15台,电风扇5台;
(3)设该业主购买空调m台,电风扇n台,空调扇p台,则10<p<20,
根据题意得:,
解得:,
∵m、n均为正整数,10<p<20,
∴p=13时,m=19,n=18符合题意,
此时总利润为:300×19+30×18+100×13=7540(元),
∵7540>7500,
∴该业主能实现目标,进货方案是:购买空调19台,电风扇18台,空调扇13台,此时获得的利润总额是7540元.
一.选择题
1.足球比赛中,每场比赛都要分出胜负每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )
A. B.
C. D.
2.小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会差25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则( )
A.他身上的钱会不足95元
B.他身上的钱会剩下95元
C.他身上的钱会不足105元
D.他身上的钱会剩下105元
3.七年级某班由于布置班级的需要,用彩纸剪出了一些“星星”和”花朵”.一张彩纸可以剪出6个“星星”或4个“花朵”,已知剪出的“星星“数量是“花朵”数量的3倍,该班级共用了10张彩纸,设用x张剪“星星”,y张剪“花朵”,根据题意,可列方程组为( )
A. B.
C. D.
4.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )
A. B.
C. D.
5.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
6.为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )
A. B.
C. D.
7.《九章算术》中有一道“盈不足术”问题,原文为:今有人共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:现有几个人共同购买一件物品,每人出8钱,则多3钱;每人出7钱,则差4钱,求物品的价格和共同购买该物品的人数.设该物品的价格是x钱,共同购买该物品的有y人,则根据题意,列出的方程组是( )
A. B.
C. D.
8.如图,将正方形ABCD的一角折叠,折痕为AE,点B恰好落在点B'处,∠B′AD比∠BAE大48°.设∠BAE和∠B′AD的度数分别为x°和y°,那么所适合的一个方程组是( )
A. B.
C. D.
9.栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?歌谣大意是:一群乌鸦落在一片树上,如果三个乌鸦落在一棵树上,那么就有五个乌鸦没有树可落;如果五个乌鸦落在一棵树上,那么就有一棵树没有落乌鸦,请问乌鸦和树各多少?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B.
C. D.
10.《孙子算经》是我国古代数学名著之一,里面有一个“二人持钱的问题,其题意是有甲、乙两人所带钱数量不详,甲若得到乙所带钱数的一半,甲的钱数就达到48,乙若得到甲所带钱数的,乙的钱数也将达到48,问甲、乙两人原来各带多少钱?若设甲、乙两人原来各带的钱数分则是x和y,小明和小伟所列方程细分别是:小明:小伟:则关于所列方程组,下列说法正确的是( )
A.小明对,小伟不对 B.小明不对,小伟对
C.两人都不对 D.两人都对
二.填空题
11.若k个连续正整数之和为2010,则k的最大值是 .
12.学生问老师:“您今年多大了”老师风趣地说:“我像你这么大时,你刚1岁;你到我这么大时,我已37岁了”.那么老师现在的年龄是 岁.
13.如图,把一个长21cm、宽15cm的长方形分成五块,其中两个大正方形和两个长方形形状和大小完全相同,那么中间小正方形的面积是 cm2.
14.如图,在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,AB=14cm,AE=6cm,则图中阴影部分的总面积是 .
15.小颖家离学校1200米,其中有一段为上坡路,另一段为下坡路.她去学校共用了16分钟,已知小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时,去时上坡路和下坡路分别是多少千米?设去时上坡路x千米,下坡路y千米,则可列方程组: .
三.解答题
16.现有36卷相同的布料做工作服,每卷布料可制作成上衣25件,或者制作成裤子40件,一件上衣和两件裤子组成一套,问,用多少卷布料制作上衣,多少卷布料制作裤子可以使上衣和裤子正好配套?
17.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒,现有正方形纸板300张,长方形纸板700张,若这些纸板恰好用完,则可做横式、竖式两种纸盒各多少个?
18.今年学校举行足球联赛,在第一阶段的比赛中,每队都进行了8场比赛,小虎足球队胜了4场,平2场,负2场,得14分;小豹足球队胜了6场,平1场,负1场,得19分.已知,记分规则中,负1场得0分.
(1)求胜1场、平1场各得多少分?
(2)足球联赛结束后,小狮足球队共参加了17场比赛,得了24分,且踢平场数是所胜场数的正整数倍,请你想一想,小狮足球队所负场数有 种可能性.
19.某电器经营业主计划购进一批同种型号的空调和电风扇,若购进8台空调和20台电风扇,需要资金23600元;若购进10台空调和30台电风扇,需要资金31000元.
(1)空调和电风扇每台的采购价各是多少元?
(2)由于国家大力推行家电下乡政策,每台空调可以比采购价下调15%,每台电风扇可以比采购价打七折.该业主计划用29930元购进两种电器共20台,其中空调不少于13台,该业主能否实现购买计划?如能实现,请帮他列出购买计划;如不能,请说明理由.
(3)该业主计划增加购买单价为每台600元的空调扇,且三种电器的总数量共50台,空调扇总数10至20台之间(不包含10、20),恰好投入55000元.若最终实际利润为,每台空调300元,每台电扇30元,每台空调扇100元.该业主决定将本次购买计划的全部利润对口捐给某医院,助益抵抗新冠肺炎疫情,现医院有7500元资金缺口.该业主能否实现目标?如果能,请直接写出进货方案和获得的利润总额.
参考答案与试题解析
一.选择题
1.【解答】解:设这个队胜x场,负y场,
根据题意,得.
故选:A.
2.【解答】解:设签字笔的单价为x元,笔记本的单价为y元,
根据题意得:20x+15y﹣25=19x+13y+15,
整理得:x+2y=40,
∵小江购买17支签字笔和9本笔记本的钱为17x+9y,
∴19x+13y+15﹣(17x+9y)
=2x+4y+15
=2(x+2y)+15
=2×40+15
=95,
即小江身上的钱会剩下95元;
故选:B.
3.【解答】解:设用x张剪“星星”,y张剪“花朵”,根据题意,可列方程组为.
故选:A.
4.【解答】解:由题意可得,
,
故选:A.
5.【解答】解:设小长方形的长为xcm,宽为ycm,
依题意,得:,
解得:,
∴14×(6+2×2)﹣6×8×2=44(cm2).
故选:A.
6.【解答】解:设A工程小组整治河道x米,B工程小组整治河道y米,依题意可得:
,
故选:A.
7.【解答】解:设该物品的价格是x钱,共同购买该物品的有y人,
依题意,得:.
故选:B.
8.【解答】解:设∠BAE和∠B′AD的度数分别为x°和y°,
根据题意可得:.
故选:D.
9.【解答】解:设诗句中谈到的鸦为x只,树为y棵,则可列出方程组为:
.
故选:D.
10.【解答】解:设甲、乙两人原来各带的钱数分则是x和y,
根据题意,得:
所以小伟的正确,小明的错误.
故选:B.
二.填空题(共5小题)
11.【解答】解:设第一个正整数是a,则第k个正整数是a+k﹣1.
根据题意,得
a+a+1+…+a+k﹣1=2010,
=2010,
k2+(2a﹣1)k=4020,
k2+(2a﹣1)k﹣4020=0,
(k+)2=4020+,
因为a,k都是正整数,要求k的最大值,则a越小越好,则﹣4020=﹣60×67,
即此时a的最小值是4,k的最大值是60.
12.【解答】解;设老师现在x岁,学生现在y岁,则
解得
答:老师现在25岁.
故填25.
13.【解答】解:设大正方形的边长为xcm,设小正方形的边长为ycm,根据题意得:
,
解得:,
故小正方形的面积=3×3=9(cm2).
故答案为:9.
14.【解答】解:设小长方形的长为xcm,宽为ycm,
依题意得:,
解得:,
∴图中阴影部分的总面积=14×(6+2y)﹣6xy=14×(6+2×2)﹣6×8×2=44(cm2).
故答案为:44cm2.
15.【解答】解:可根据所用时间和所走的路程和得到相应的方程组为:,
故答案为:.
三.解答题(共4小题)
16.【解答】解:设用x卷布料制作上衣,y卷布料制作裤子可以使上衣和裤子正好配套,
依题意,得:,
解得:.
答:用16卷布料制作上衣,20卷布料制作裤子可以使上衣和裤子正好配套.
17.【解答】解:设可做横式纸盒x个,可做竖式纸盒y个,依题意有
,
解得.
故可做横式纸盒100个,可做竖式纸盒100个.
18.【解答】解:(1)设胜1场得x分,平1场得y分,
由题意得,
解得.
答:胜1场得3分,平1场得1分;
(2)设小狮足球队胜m场,平n场,负t场,
依题意得:,
∴n=24﹣3m,t=2m﹣7.
∵n是m的正整数倍,t≥0及m为整数,
∴m=4,n=12或m=6,n=6.
∴小狮足球队所负场数有 2种可能性.
故答案为:2.
19.【解答】解:(1)设空调每台的采购价是x元,电风扇每台的采购价是y元,
根据题意得:,
解得:.
答:空调每台的采购价是2200元,电风扇每台的采购价是300元;
(2)由题意得,每台空调的采购价为2200×(1﹣15%)=1870(元),每台电风扇的采购价为300×0.7=210(元).
设该业主购买空调a台,则购买电风扇(20﹣a)台,
根据题意得:,
解得:13≤a≤15.5,
∵a是整数,
∴a=13,14,15.
故该业主能实现购买计划,购买计划有三种:
①购买空调13台,电风扇7台;
②购买空调14台,电风扇6台;
③购买空调15台,电风扇5台;
(3)设该业主购买空调m台,电风扇n台,空调扇p台,则10<p<20,
根据题意得:,
解得:,
∵m、n均为正整数,10<p<20,
∴p=13时,m=19,n=18符合题意,
此时总利润为:300×19+30×18+100×13=7540(元),
∵7540>7500,
∴该业主能实现目标,进货方案是:购买空调19台,电风扇18台,空调扇13台,此时获得的利润总额是7540元.
