17.1 勾股定理(1)课件(共24张PPT)
文档属性
| 名称 | 17.1 勾股定理(1)课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:00:44 | ||
图片预览





文档简介
(共24张PPT)
人教版
八年级数学上
17.1.1勾股定理(1)
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理的一
些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.(重点)
2.会用勾股定理进行简单的计算
.(难点)
情境导入
在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股。斜边叫做弦。
据我国古算书《周髀算经》记载,约公元前1100年,人们已经知道,如果勾是三、股是四,那么弦是五。后来人们进一步发现并证明了直角三角形三边之间的关系:两条直角边的平方和等于斜边的平方。
情境导入
上面的图案有什么意义?为什么选它作为2002年在北京召开的国际数学家大会的会徽?
学过本章,你就能回答上述问题了。本章中,我们将探索直角三角形的三边之间特有的数量关系,并运用所得结论解决问题。
ICM
2002
Beijing
August
20-28.
2002
合作探究---勾股定理
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1
试问正方形A、B、C面积之间有什么样的数量关系?
合作探究---勾股定理
A
B
C
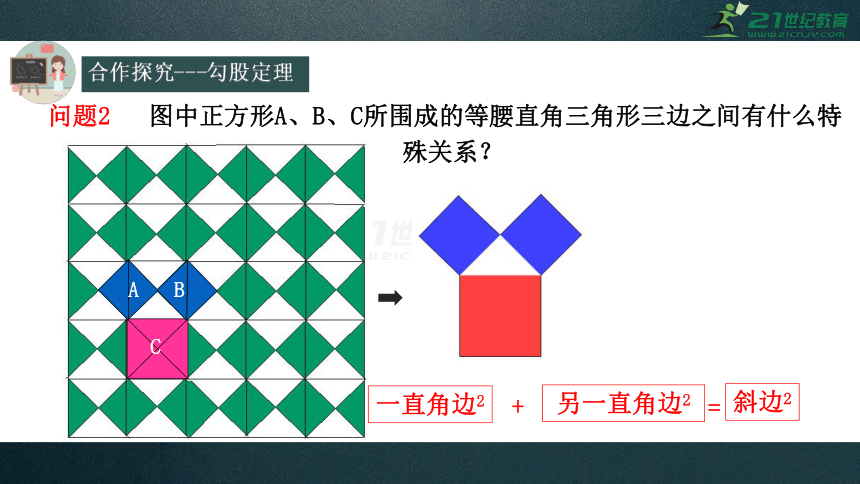
一直角边2
另一直角边2
斜边2
+
=
问题2
图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特
殊关系?
合作探究---勾股定理
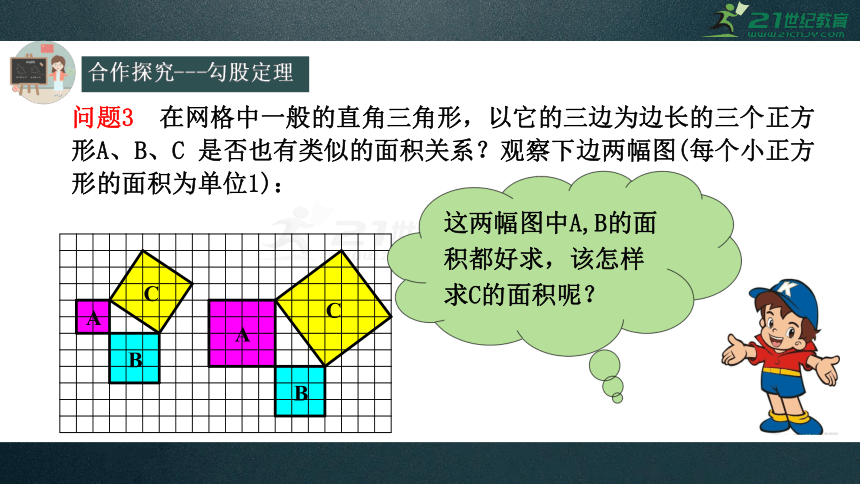
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C
是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
合作探究---勾股定理
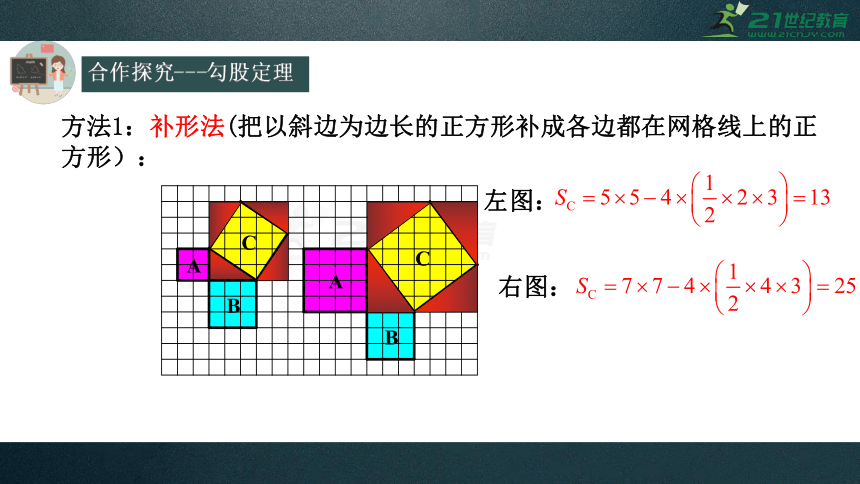
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
合作探究---勾股定理
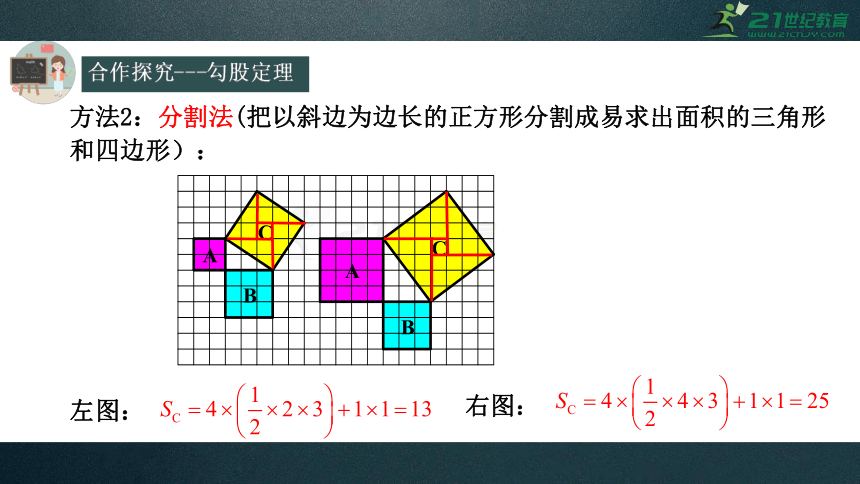
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
合作探究---勾股定理
根据前面求出的C的面积直接填出下表:
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考
正方形A、B、C
所围成的直角三角形三条边之间有怎样的特殊关系?
合作探究---勾股定理
命题1
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
合作探究---勾股定理
下边的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实。加差实,亦成弦实。
即:四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形
(黄色)。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
合作探究---勾股定理
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
b
c
a
b
a
c
合作探究---勾股定理
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵
爽
弦
图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
合作探究---勾股定理
(a、b、c为正数)
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
典例精析
例1
如图,在Rt△ABC中,
∠C=90°.
(1)若a=6,c=10,求b;
(2)若a=5,b=12,求c.
解:
(1)据勾股定理得:
(2)据勾股定理得:
C
A
B
(3)若c=25,b=15,求a.
(3)据勾股定理得:
小试牛刀
1.下列说法中,正确的是(
)
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为
.
8
cm
10
cm
36
cm?
小试牛刀
3、求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
小试牛刀
(1)若a:b=1:2
,c=10,求a;
(2)若b=15,∠A=30°,求a,c.
4、在Rt△ABC中,
∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=102,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
知识点拨:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
小试牛刀
5、
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
知识点拨:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
能力提升
解:∵AE=BE,
∴S△ABE=
AE·BE=
AE2.
根据勾股定理得:AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
根据勾股定理得:
AC2+BC2=AB2,
∴阴影部分的面积为
AB2=
.
6.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
课堂小结
本节课你有哪些收获?
1、什么是勾股定理?
2、运用勾股定理需要注意什么?
课后作业
教材28页习题17.1第1、7、8题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
17.1.1勾股定理(1)
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理的一
些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.(重点)
2.会用勾股定理进行简单的计算
.(难点)
情境导入
在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股。斜边叫做弦。
据我国古算书《周髀算经》记载,约公元前1100年,人们已经知道,如果勾是三、股是四,那么弦是五。后来人们进一步发现并证明了直角三角形三边之间的关系:两条直角边的平方和等于斜边的平方。
情境导入
上面的图案有什么意义?为什么选它作为2002年在北京召开的国际数学家大会的会徽?
学过本章,你就能回答上述问题了。本章中,我们将探索直角三角形的三边之间特有的数量关系,并运用所得结论解决问题。
ICM
2002
Beijing
August
20-28.
2002
合作探究---勾股定理
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1
试问正方形A、B、C面积之间有什么样的数量关系?
合作探究---勾股定理
A
B
C
一直角边2
另一直角边2
斜边2
+
=
问题2
图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特
殊关系?
合作探究---勾股定理
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C
是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
合作探究---勾股定理
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
合作探究---勾股定理
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
合作探究---勾股定理
根据前面求出的C的面积直接填出下表:
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考
正方形A、B、C
所围成的直角三角形三条边之间有怎样的特殊关系?
合作探究---勾股定理
命题1
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
合作探究---勾股定理
下边的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实。加差实,亦成弦实。
即:四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形
(黄色)。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
合作探究---勾股定理
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
b
c
a
b
a
c
合作探究---勾股定理
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵
爽
弦
图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
合作探究---勾股定理
(a、b、c为正数)
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
典例精析
例1
如图,在Rt△ABC中,
∠C=90°.
(1)若a=6,c=10,求b;
(2)若a=5,b=12,求c.
解:
(1)据勾股定理得:
(2)据勾股定理得:
C
A
B
(3)若c=25,b=15,求a.
(3)据勾股定理得:
小试牛刀
1.下列说法中,正确的是(
)
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为
.
8
cm
10
cm
36
cm?
小试牛刀
3、求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
小试牛刀
(1)若a:b=1:2
,c=10,求a;
(2)若b=15,∠A=30°,求a,c.
4、在Rt△ABC中,
∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=102,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
知识点拨:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
小试牛刀
5、
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
知识点拨:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
能力提升
解:∵AE=BE,
∴S△ABE=
AE·BE=
AE2.
根据勾股定理得:AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
根据勾股定理得:
AC2+BC2=AB2,
∴阴影部分的面积为
AB2=
.
6.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
课堂小结
本节课你有哪些收获?
1、什么是勾股定理?
2、运用勾股定理需要注意什么?
课后作业
教材28页习题17.1第1、7、8题.
https://www.21cnjy.com/help/help_extract.php
