北师大版八年级下册数学 5.2分式的分母是单项式的通分 练习(word版含解析)
文档属性
| 名称 | 北师大版八年级下册数学 5.2分式的分母是单项式的通分 练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 09:06:30 | ||
图片预览

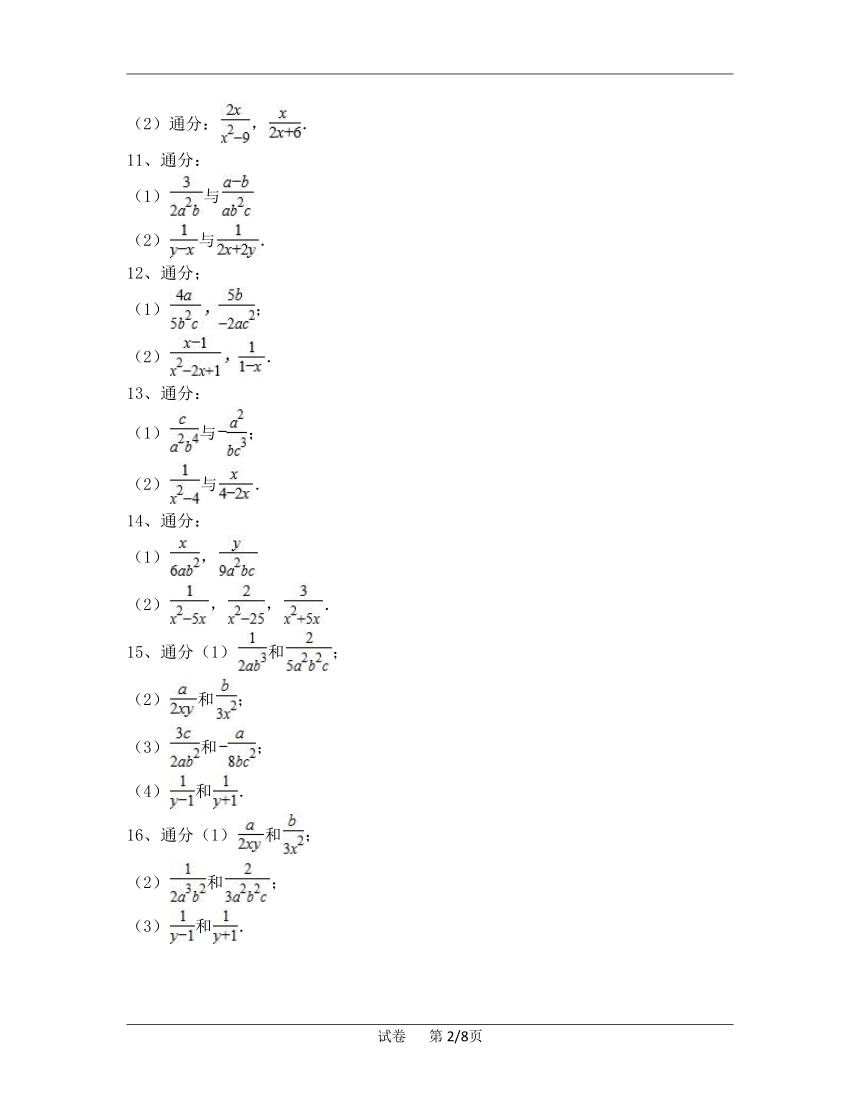
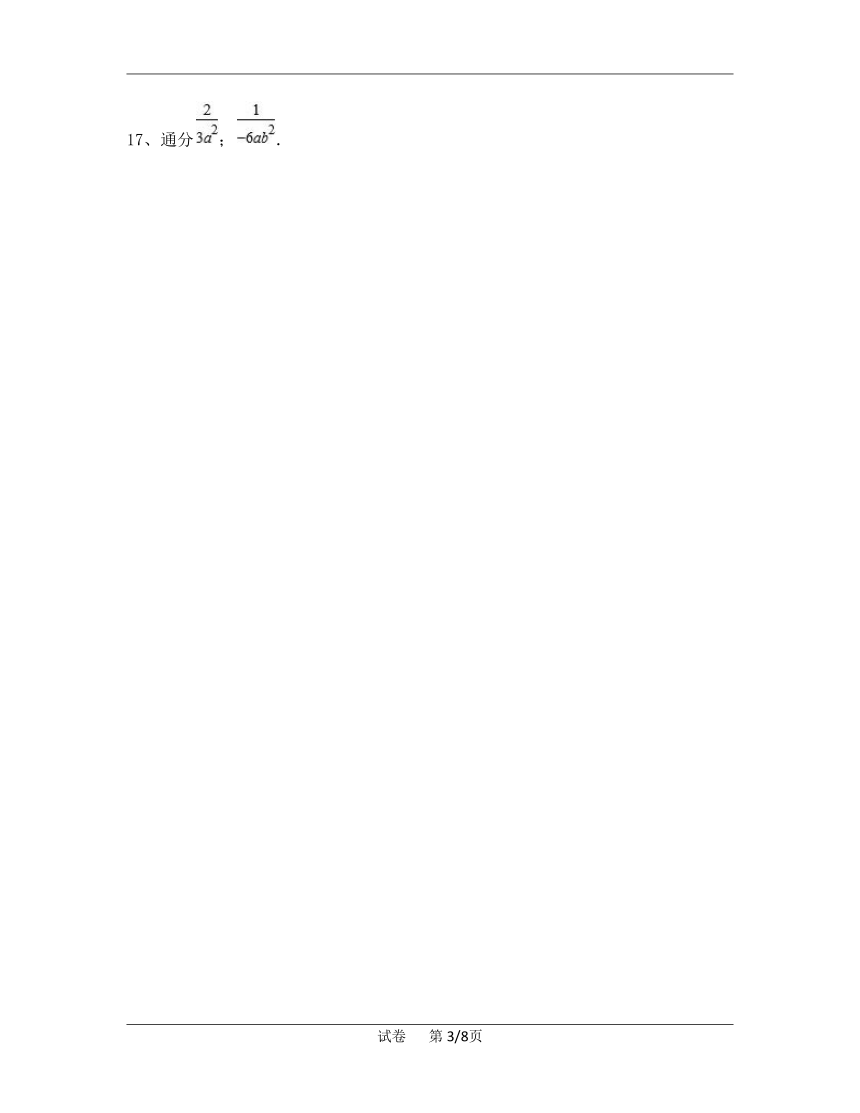

文档简介
分式的分母是单项式的通分
一、填空题
1、分式,,的最简公分母是__________
2、分式,,的最简公分母是
__________
.
3、把分式,,通分后,结果是__________.
4、将,通分可得__________.
5、将通分后的结果分别为__________.
6、将通分后,它们分别是__________,__________,__________.
二、解答题
7、通分:
(1),,
(2),.
8、
通分:
(1);
(2)
9、通分:和-.
10、(1)通分:,-;
(2)通分:,.
11、通分:
(1)与
(2)与.
12、通分;
(1);
(2).
13、通分:
(1)与;
(2)与.
14、通分:
(1),
(2),,.
15、通分(1)和;
(2)和;
(3)和;
(4)和.
16、通分(1)和;
(2)和;
(3)和.
17、通分;.
试卷
第4/8页
分式的分母是单项式的通分的答案和解析
一、填空题
1、答案:
12b
试题分析:
通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母。
解:因为三分式中的常数项系数的最小公倍数是12,a的最高次幂次数是2,b的最高次幂次数是1,所以三分式的最简公分母是12b.
故答案为:12b.
2、答案:
试题分析:确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
试题解析:分式,,的分母分别是3a2b2、-4b4c、2a2c,故最简公分母是12a2b4c;
故答案为12a2b4c.
3、答案:
试题分析:先找出三个分式的最简公分母,再根据分式的基本性质进行解答即可.
试题解析:=,
=,
=.
故答案为:,,.
4、答案:
试题分析:将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂.
试题解析:∵两个分式分母分别为3a,2c未知数系数的最小公倍数为3×2=6,
∵a,c的最高次数为1,
∴最简公分母为6ac,将,通分可得:和.
5、答案:
试题分析:解答此题的关键是求出最简公分母,然后再进行通分.
试题解析:(1)的最简公分母为12xy2,
故;;.
故答案为:.
6、答案:
试题分析:先确定三个分式的最简公分母是3ab,可得通分后的结果.
试题解析:由三个分式的最简公分母是3ab,故通分后它们分别是:.
二、解答题
7、答案:
试题分析:(1)先找出这三项的最简公分母10a2b2c2,再进行通分即可;
(2)将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂.
试题解析:(1)=,
=,
=-;
(2)=,=-.
8、答案:
解:(1);
(2)
试题分析:
找出两式的最简公分母,通分即可。
试题解析:
9、答案:
试题分析:先找出最简公分母,再根据分式的基本性质通分即可.
试题解析:最简公分母是:8ab2c2,
==;
-=-=-.
10、答案:
试题分析:(1)、(2)找到最简公分母,分子、分母同时乘以分母中缺少的项,即可通分.
试题解析:(1)分母3a2,bc的最简公分母是3a2bc,
==;
-=-=-;
(2)x2-9=(x-3)(x+3),2x+6=2(x+3),
它们的最简公分母是2(x-3)(x+3),
==;
==.
11、答案:
试题分析:(1)找出最简公分母,通分即可得到结果;
(2)找出最简公分母,通分即可得到结果.
试题解析:(1)=,=;
(2)=-,=.
12、答案:
试题分析:(1)先找出两式的最简公分母,再根据等式的性质进行解答即可;
(2)先把第一个式子进行因式分解,再约分,得到的结果再与第二个式子找出最简公分母即可.
试题解析:(1)=,=-;
(2)==;=-.
13、答案:
试题分析:(1)找出两式的最简公分母,再进行通分即可;
(2)先把两式进行因式分解,再进行通分,即可得出答案.
试题解析:(1)=,-=-;
(2)==,=-=-;
14、答案:
试题分析:通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.找出分式的最简公分母,然后通分即可得出答案.
试题解析:(1)=,
=;
(2)=,
=,
=.
15、答案:
试题分析:解答此题的关键是求出公分母,再通分.
试题解析:(1)两式的最简公分母为10a2b3c,
故=,=;
(2)两式的最简公分母为6x2y,
故=,,
(3)两式的最简公分母为8ab2c2,
故=,,
(4)两式的最简公分母为y2-1,
故=,.
16、答案:
试题分析:解答此题的关键是求出最简公分母,然后再进行通分.
试题解析:(1)两式的最简公分母为6x2y,
故=、=;
(2)两式的最简公分母为6a3b2c,
故=、=;
(3)两式的最简公分母为y2-1,
故=、=.
17、答案:
试题分析:通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.所以两分式的最简公分母为6a2b2,然后通分即可.
试题解析:两分式的最简公分母为6a2b2,
通分得:=;
==.
一、填空题
1、分式,,的最简公分母是__________
2、分式,,的最简公分母是
__________
.
3、把分式,,通分后,结果是__________.
4、将,通分可得__________.
5、将通分后的结果分别为__________.
6、将通分后,它们分别是__________,__________,__________.
二、解答题
7、通分:
(1),,
(2),.
8、
通分:
(1);
(2)
9、通分:和-.
10、(1)通分:,-;
(2)通分:,.
11、通分:
(1)与
(2)与.
12、通分;
(1);
(2).
13、通分:
(1)与;
(2)与.
14、通分:
(1),
(2),,.
15、通分(1)和;
(2)和;
(3)和;
(4)和.
16、通分(1)和;
(2)和;
(3)和.
17、通分;.
试卷
第4/8页
分式的分母是单项式的通分的答案和解析
一、填空题
1、答案:
12b
试题分析:
通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母。
解:因为三分式中的常数项系数的最小公倍数是12,a的最高次幂次数是2,b的最高次幂次数是1,所以三分式的最简公分母是12b.
故答案为:12b.
2、答案:
试题分析:确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
试题解析:分式,,的分母分别是3a2b2、-4b4c、2a2c,故最简公分母是12a2b4c;
故答案为12a2b4c.
3、答案:
试题分析:先找出三个分式的最简公分母,再根据分式的基本性质进行解答即可.
试题解析:=,
=,
=.
故答案为:,,.
4、答案:
试题分析:将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂.
试题解析:∵两个分式分母分别为3a,2c未知数系数的最小公倍数为3×2=6,
∵a,c的最高次数为1,
∴最简公分母为6ac,将,通分可得:和.
5、答案:
试题分析:解答此题的关键是求出最简公分母,然后再进行通分.
试题解析:(1)的最简公分母为12xy2,
故;;.
故答案为:.
6、答案:
试题分析:先确定三个分式的最简公分母是3ab,可得通分后的结果.
试题解析:由三个分式的最简公分母是3ab,故通分后它们分别是:.
二、解答题
7、答案:
试题分析:(1)先找出这三项的最简公分母10a2b2c2,再进行通分即可;
(2)将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂.
试题解析:(1)=,
=,
=-;
(2)=,=-.
8、答案:
解:(1);
(2)
试题分析:
找出两式的最简公分母,通分即可。
试题解析:
9、答案:
试题分析:先找出最简公分母,再根据分式的基本性质通分即可.
试题解析:最简公分母是:8ab2c2,
==;
-=-=-.
10、答案:
试题分析:(1)、(2)找到最简公分母,分子、分母同时乘以分母中缺少的项,即可通分.
试题解析:(1)分母3a2,bc的最简公分母是3a2bc,
==;
-=-=-;
(2)x2-9=(x-3)(x+3),2x+6=2(x+3),
它们的最简公分母是2(x-3)(x+3),
==;
==.
11、答案:
试题分析:(1)找出最简公分母,通分即可得到结果;
(2)找出最简公分母,通分即可得到结果.
试题解析:(1)=,=;
(2)=-,=.
12、答案:
试题分析:(1)先找出两式的最简公分母,再根据等式的性质进行解答即可;
(2)先把第一个式子进行因式分解,再约分,得到的结果再与第二个式子找出最简公分母即可.
试题解析:(1)=,=-;
(2)==;=-.
13、答案:
试题分析:(1)找出两式的最简公分母,再进行通分即可;
(2)先把两式进行因式分解,再进行通分,即可得出答案.
试题解析:(1)=,-=-;
(2)==,=-=-;
14、答案:
试题分析:通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.找出分式的最简公分母,然后通分即可得出答案.
试题解析:(1)=,
=;
(2)=,
=,
=.
15、答案:
试题分析:解答此题的关键是求出公分母,再通分.
试题解析:(1)两式的最简公分母为10a2b3c,
故=,=;
(2)两式的最简公分母为6x2y,
故=,,
(3)两式的最简公分母为8ab2c2,
故=,,
(4)两式的最简公分母为y2-1,
故=,.
16、答案:
试题分析:解答此题的关键是求出最简公分母,然后再进行通分.
试题解析:(1)两式的最简公分母为6x2y,
故=、=;
(2)两式的最简公分母为6a3b2c,
故=、=;
(3)两式的最简公分母为y2-1,
故=、=.
17、答案:
试题分析:通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.所以两分式的最简公分母为6a2b2,然后通分即可.
试题解析:两分式的最简公分母为6a2b2,
通分得:=;
==.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
