11.2.1三角形全等判定(1)sss
文档属性
| 名称 | 11.2.1三角形全等判定(1)sss |  | |
| 格式 | rar | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 19:44:01 | ||
图片预览








文档简介
(共31张PPT)
旬阳县棕溪初中 薛玉梅
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办
数据能尽可能少吗?
A
B
C
D
E
F
1、能够( )的两个三角形叫全等三角形。
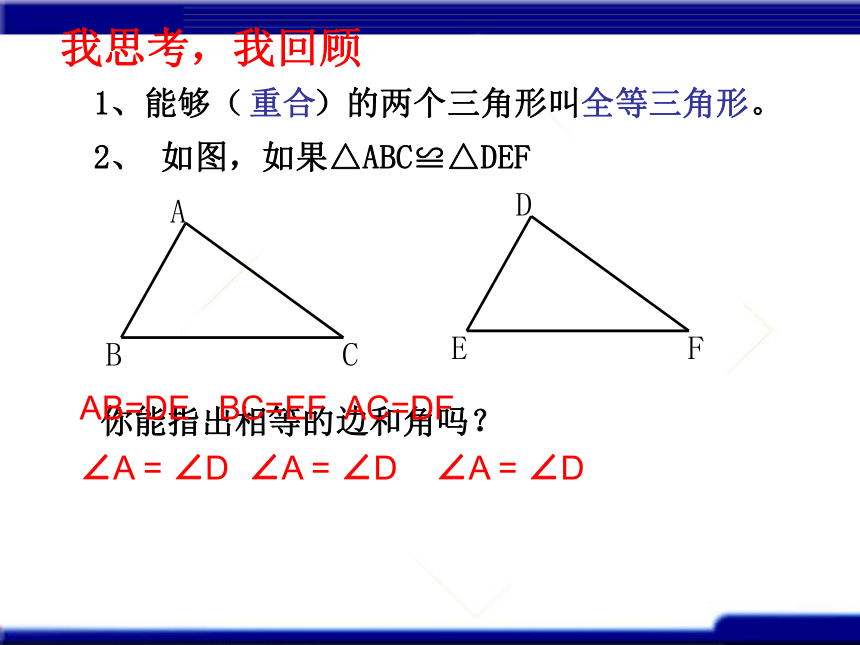
2、 如图,如果△ABC≌△DEF
重合
我思考,我回顾
你能指出相等的边和角吗?
AB=DE BC=EF AC=DF
∠A = ∠D ∠A = ∠D ∠A = ∠D
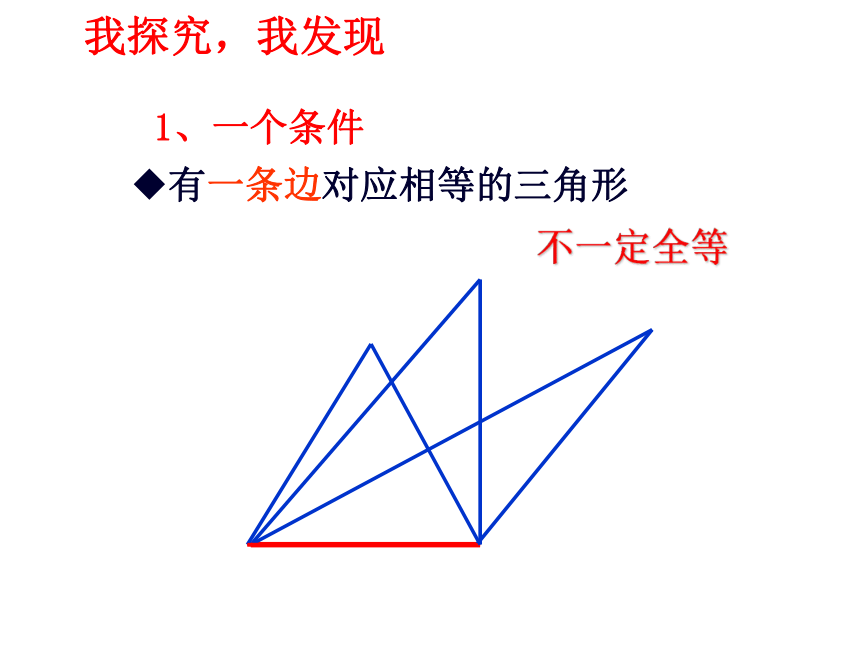
1、一个条件
有一条边对应相等的三角形
不一定全等
我探究,我发现
有一个角对应相等的三角形
不一定全等
一个条件
不能保证三角形全等
我探究,我发现
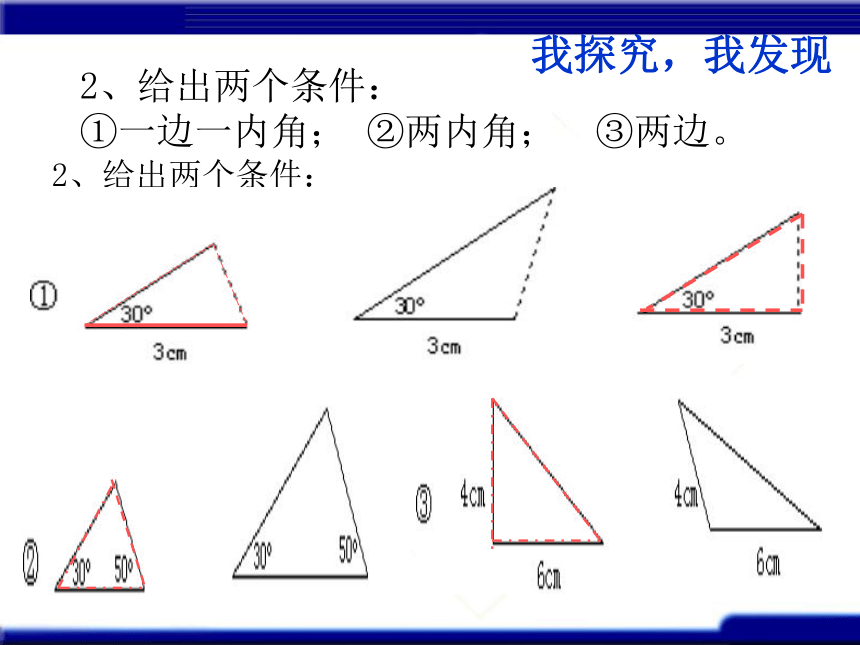
2、给出两个条件:
①一边一内角; ②两内角; ③两边。
2、给出两个条件:
①一边一内角; ②两内角; ③两边。
我探究,我发现
3.给出三个条件
(1)三条边
(2)三个角
(3)两角一边
(4)两边一角
我猜测,我探究
你会用刻度尺和圆规画△ DEF吗?使其三边分别为3cm,4cm和5cm。
把你画的三角形与同桌同学所画的三角形剪下来,进行比较,它们能否互相重合?
1、画线段EF= 3cm。
2、分别以E、F为圆心, 5cm , 4cm
长为半径画弧,两弧交于点D。
3、连结DE,DF。
△ DEF就是所求的三角形
作法:
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, B/C/ =BC,A/C/ =AC。把画好的△A/B/C/剪下来,放到△ABC上,它们重合吗?
(活动要求:就近四人一组,组内自选小组长,先讨论确定三角形三边长,按照所确定的统一标准各自在练习本上画一个三角形,然后将所画的三角形剪下来,由小组长收集起来后再叠放在一起,看看有什么发现?5分钟后组长代表小组交流)
思考:如果按照你们选定的条件画8个、10个、16个、…n个三角形,并将其剪下来叠放在一起,结果会怎样呢?你们由此可以得到什么结论?谁能将这个结论用语言表述出来?
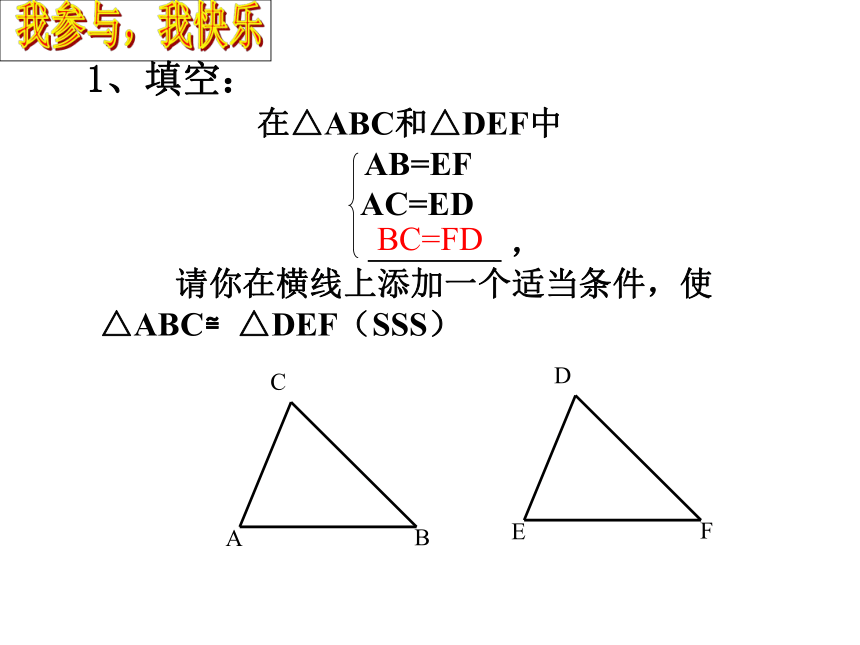
在△ABC和△DEF中
AB=EF
AC=ED
,
请你在横线上添加一个适当条件,使△ABC≌△DEF(SSS)
1、填空:
D
E
F
C
A
B
BC=FD
2、如下图,AD=BC,添加适当的条件△ABD≌△CDB
__________。
A
B
C
D
3、你还能从2题中获得的结论是______________。
AB=CD
AD=BC
BD=DB
AB=CD
1、如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD
2、除△ABD≌△ACD外,你还能得到哪些结论?为什么
1、工人师傅常用角尺平分一个任意角。作法如下:已知∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
2、学习了本节课以后,善于总结的小华说:“我能利用本节课所学习的知识来作一个角等于已知角”。其过程如下:
已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA、OB与点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′与点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB。
(1)她的作法对吗?为什么?
(2)你能作一个角等于已知角吗?试一试。
课外探究
如图,OC=OD,PC=PD,试说明 点P在∠AOB的角的平分线上。
O
A
P
B
C
D
1.学完本节课后,你有哪些收获?
2.通过本节课学习,你感觉还有需要帮助的地方是吗?
必做题:
1、阅读教材6——8页本节课所学内容。
2、习题11.2的1、2题
3、画一个三角形,使它的三边分别为3cm,4cm,3cm。
选做题:
搜集生活中运用三角形的稳定性的实例。
已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
解:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B (公共边)
∴△ACB≌△ADB
(SSS)
议一议:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
1.只给一个条件
(2)只给定一条角
我探究,我发现
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给定一条边:
②只给定一个角:
60°
60°
60°
探究一:
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
我探究,我发现
(SSS)
A
B
C
D
拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
∴ ABD ≌ CDB
∴ ∠A= ∠C ( )
全等三角形的对应角相等
有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ”
A
B
C
D
E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
一个判定方法即三边对应相等的两个三角形全等(边边边或SSS);
两种作图:一是已知三角形三条边的长度作三角形;二是作一个角等于已知角。
一种基本数学思想即分类讨论数学思想。
初步学会理解证明的思路。
1.学完本节课后,你有哪些收获?
2.通过本节课学习,你感觉还有需要帮助的地方是吗?
1.只给一个条件
(2)给定一条角
我探究,我发现
有一个角对应相等的三角形
不一定全等
A
A
A
我观察,我发现
1.只给一个条件
(1)给定一条边
(2)给定一条角
A
A
A
B
B
B
有一条边对应相等的三角形
不一定全等
旬阳县棕溪初中 薛玉梅
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办
数据能尽可能少吗?
A
B
C
D
E
F
1、能够( )的两个三角形叫全等三角形。
2、 如图,如果△ABC≌△DEF
重合
我思考,我回顾
你能指出相等的边和角吗?
AB=DE BC=EF AC=DF
∠A = ∠D ∠A = ∠D ∠A = ∠D
1、一个条件
有一条边对应相等的三角形
不一定全等
我探究,我发现
有一个角对应相等的三角形
不一定全等
一个条件
不能保证三角形全等
我探究,我发现
2、给出两个条件:
①一边一内角; ②两内角; ③两边。
2、给出两个条件:
①一边一内角; ②两内角; ③两边。
我探究,我发现
3.给出三个条件
(1)三条边
(2)三个角
(3)两角一边
(4)两边一角
我猜测,我探究
你会用刻度尺和圆规画△ DEF吗?使其三边分别为3cm,4cm和5cm。
把你画的三角形与同桌同学所画的三角形剪下来,进行比较,它们能否互相重合?
1、画线段EF= 3cm。
2、分别以E、F为圆心, 5cm , 4cm
长为半径画弧,两弧交于点D。
3、连结DE,DF。
△ DEF就是所求的三角形
作法:
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, B/C/ =BC,A/C/ =AC。把画好的△A/B/C/剪下来,放到△ABC上,它们重合吗?
(活动要求:就近四人一组,组内自选小组长,先讨论确定三角形三边长,按照所确定的统一标准各自在练习本上画一个三角形,然后将所画的三角形剪下来,由小组长收集起来后再叠放在一起,看看有什么发现?5分钟后组长代表小组交流)
思考:如果按照你们选定的条件画8个、10个、16个、…n个三角形,并将其剪下来叠放在一起,结果会怎样呢?你们由此可以得到什么结论?谁能将这个结论用语言表述出来?
在△ABC和△DEF中
AB=EF
AC=ED
,
请你在横线上添加一个适当条件,使△ABC≌△DEF(SSS)
1、填空:
D
E
F
C
A
B
BC=FD
2、如下图,AD=BC,添加适当的条件△ABD≌△CDB
__________。
A
B
C
D
3、你还能从2题中获得的结论是______________。
AB=CD
AD=BC
BD=DB
AB=CD
1、如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD
2、除△ABD≌△ACD外,你还能得到哪些结论?为什么
1、工人师傅常用角尺平分一个任意角。作法如下:已知∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
2、学习了本节课以后,善于总结的小华说:“我能利用本节课所学习的知识来作一个角等于已知角”。其过程如下:
已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA、OB与点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′与点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB。
(1)她的作法对吗?为什么?
(2)你能作一个角等于已知角吗?试一试。
课外探究
如图,OC=OD,PC=PD,试说明 点P在∠AOB的角的平分线上。
O
A
P
B
C
D
1.学完本节课后,你有哪些收获?
2.通过本节课学习,你感觉还有需要帮助的地方是吗?
必做题:
1、阅读教材6——8页本节课所学内容。
2、习题11.2的1、2题
3、画一个三角形,使它的三边分别为3cm,4cm,3cm。
选做题:
搜集生活中运用三角形的稳定性的实例。
已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
解:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B (公共边)
∴△ACB≌△ADB
(SSS)
议一议:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
1.只给一个条件
(2)只给定一条角
我探究,我发现
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给定一条边:
②只给定一个角:
60°
60°
60°
探究一:
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
我探究,我发现
(SSS)
A
B
C
D
拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
∴ ABD ≌ CDB
∴ ∠A= ∠C ( )
全等三角形的对应角相等
有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ”
A
B
C
D
E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
一个判定方法即三边对应相等的两个三角形全等(边边边或SSS);
两种作图:一是已知三角形三条边的长度作三角形;二是作一个角等于已知角。
一种基本数学思想即分类讨论数学思想。
初步学会理解证明的思路。
1.学完本节课后,你有哪些收获?
2.通过本节课学习,你感觉还有需要帮助的地方是吗?
1.只给一个条件
(2)给定一条角
我探究,我发现
有一个角对应相等的三角形
不一定全等
A
A
A
我观察,我发现
1.只给一个条件
(1)给定一条边
(2)给定一条角
A
A
A
B
B
B
有一条边对应相等的三角形
不一定全等
