北师大版八年级数学上册课件:5.6二元一次方程与一次函数(共22张PPT)
文档属性
| 名称 | 北师大版八年级数学上册课件:5.6二元一次方程与一次函数(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:24:17 | ||
图片预览






文档简介
x+y=5是什么?
5.6 二元一次方程与一次函数
向正华
一次函数
这是怎么回事?
二元一次方程
方程 x+y=5可以转化为
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
归纳:
思考:是不是任意的二元一次方程都能进行这样的转换呢?
y=5-x
师生互动
(1)方程x+y=5的解有 个解,
例如: 。
(2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=5-x上吗?
(0,5) 、(5,0) 、(1,4) .都在函数y=5-x的图象上.
(0,5) 、(5,0) 、(1,4)......
无数
师生互动
过(0,5) 、(5,0) 两点的直线图象与一次函数y=5-x的图象相同.
(4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=5-x的图象相同吗?
在一次函数y=5-x的图象上任取一个点(0,5),它的坐标适合方程x+y=5.
(3)在一次函数y=5-x的图象上任取一个点,它的坐标适合方程x+y=5吗?
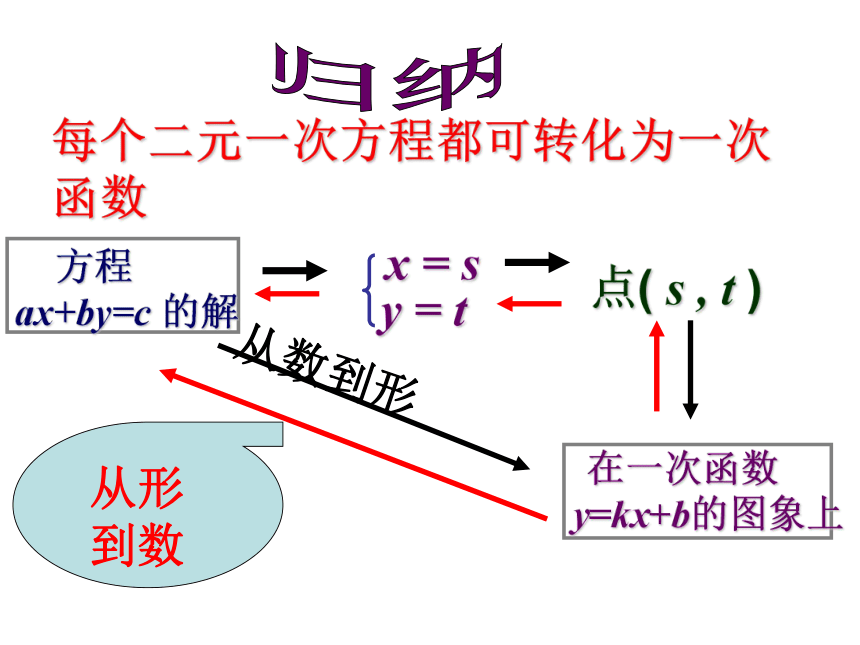
在一次函数
y=kx+b的图象上
点( s , t )
x = s
y = t
方程
ax+by=c 的解
从形到数
从数到形
每个二元一次方程都可转化为一次函数
y=5-x
y=2x-1
x=0
y=5
x=5
y=0
x=0
y=-1
x=0.5
y=0
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=2x-1
y=5-x
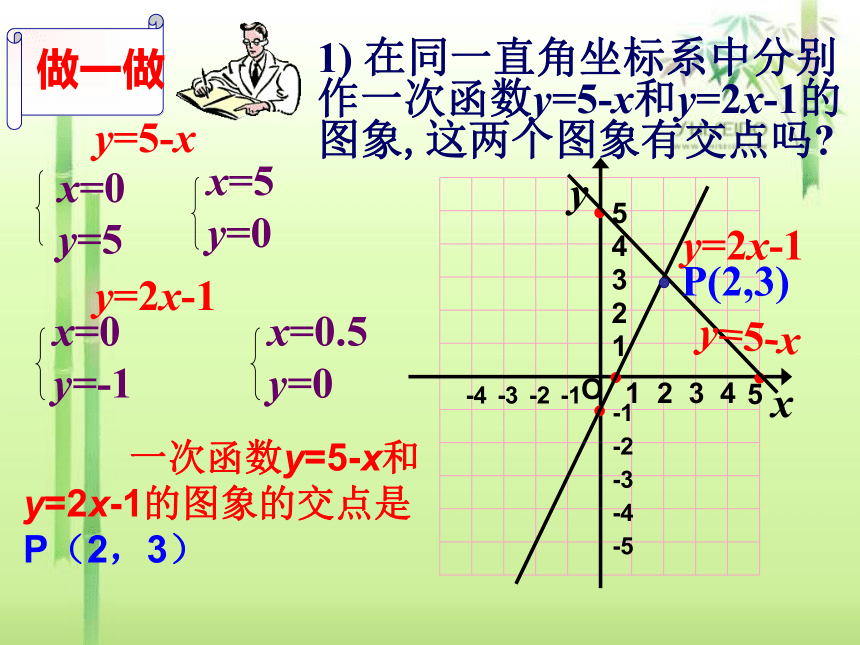
P(2,3)
做一做
1) 在同一直角坐标系中分别作一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?
5
一次函数y=5-x和y=2x-1的图象的交点是P(2,3)
2)方程组 的解是多少 ?
{
x+y=5,
2x-y=1.
交点坐标(2,3)是方程组 的解。
{
x+y=5
2x-y=1
x+y=5
2x-y=1
x=2
y=3
的解
3) 一次函数y=5-x和y=2x-1的图象的交点
坐标(2,3)与方程组 的解有什么关系?
{
x+y=5;
2x-y=1
一般地,从图形的角度看,确定两条直线交点的
坐标,相当于求相应的二元一次方程组的解;解一个二
元一次方程组相当于确定相应两条直线交点的坐标。
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
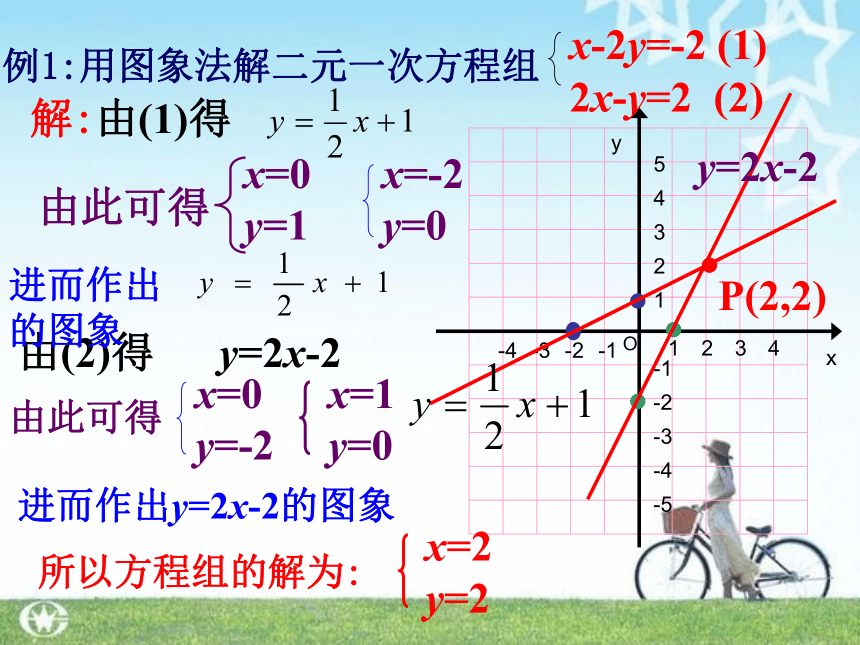
P(2,2)
y=2x-2
x=2
y=2
所以方程组的解为:
由(2)得 y=2x-2
x=0
y=-2
x=1
y=0
由此可得
进而作出y=2x-2的图象
x=0
y=1
x=-2
y=0
由此可得
解:由(1)得
进而作出 的图象
x-2y=-2 (1)
2x-y=2 (2)
例1:用图象法解二元一次方程组
(1)对应关系
①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③由交点坐标得出方程组的解.
二元一次方程组的解
两个一次函数图象的交点坐标
两个一次函数
(2)图象法解方程组的步骤:
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为
则函数 与 的图象的交点
坐标为 .
(2,2)
3.根据下列图象,你能说出是哪些方程组的解?这些解是什么?
1
1
x
y
0
-2
1
x
y
0
x
3
2
1
-1
-2
y
-2
2
-1
0
1
3
在同一直角坐标系内, 一次函数y = x + 1 和
y = x - 2 的图象有怎样的位置关系?
方程组
解的情况如何?
你发现了什么?
2.方程组 当 时,
方程组无解;反之也成立。
1.两直线
当 平行于 时, ;反之也成立。
求直线 与 直线的交点坐标。你有哪些方法?与同伴交流,并一起分析各种方法的利弊.
解法思路2:由解方程组,得到交点坐标.(把形的问题归结为数的解决,便捷准确)
解法思路l:画出图象找出交点,确定交点坐标近似值.(因作图误差可能有较大差别)
十七世纪法国数学家笛卡尔有一次生病卧床,他看见屋顶上的一只蜘蛛顺着左右爬行,笛卡尔看到蜘蛛的“表演”猛的灵机一动。他想,可以把蜘蛛看成一个点,它可以上、下、左、右运动,能不能知道蜘蛛的位置用一组数确定下来呢?
在蜘蛛爬行的启示下,笛卡尔创建了直角坐
标系,直角坐标系的创建,在代数和几何上架
起了一座桥梁。在坐标系下几何图形(形)
和方程(数)建立了联系。笛卡尔坐标系起
到了桥梁和纽带的作用,而我们可以把图形
化成方程来研究,也可以用图象来研究方程。
这节课我们就来研究二元一次方程(组)
与一次函数(形)的关系。
知识源于悟
益智的“机会”
师:通过以上结论,你能分析研究出二元一次方程与一次函数图象的关系吗?
生:二元一次方程的解就是一次函数图象的点的 坐标;一次函数图象上的点的坐标就是二元一次方程的解.
二元一次方程与一次函数的基本关系
知识的升华
小结 拓展
1) 二元一次方程与一次函数的关系 :
二元一次方程的解是一次函数上点的坐标; 一次函数上每一个点的坐标就是二元一次方程的一组解.
2) 二元一次方程组的解法总共学习了哪几种?
加减法;代入法;图象法.
3) 方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要用代 数方法,进行细致计算.
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
从函数角度解释:
作业
1、习题5.7;
2、相关资料书的习题。
5.6 二元一次方程与一次函数
向正华
一次函数
这是怎么回事?
二元一次方程
方程 x+y=5可以转化为
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
归纳:
思考:是不是任意的二元一次方程都能进行这样的转换呢?
y=5-x
师生互动
(1)方程x+y=5的解有 个解,
例如: 。
(2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=5-x上吗?
(0,5) 、(5,0) 、(1,4) .都在函数y=5-x的图象上.
(0,5) 、(5,0) 、(1,4)......
无数
师生互动
过(0,5) 、(5,0) 两点的直线图象与一次函数y=5-x的图象相同.
(4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=5-x的图象相同吗?
在一次函数y=5-x的图象上任取一个点(0,5),它的坐标适合方程x+y=5.
(3)在一次函数y=5-x的图象上任取一个点,它的坐标适合方程x+y=5吗?
在一次函数
y=kx+b的图象上
点( s , t )
x = s
y = t
方程
ax+by=c 的解
从形到数
从数到形
每个二元一次方程都可转化为一次函数
y=5-x
y=2x-1
x=0
y=5
x=5
y=0
x=0
y=-1
x=0.5
y=0
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=2x-1
y=5-x
P(2,3)
做一做
1) 在同一直角坐标系中分别作一次函数y=5-x和y=2x-1的图象,这两个图象有交点吗?
5
一次函数y=5-x和y=2x-1的图象的交点是P(2,3)
2)方程组 的解是多少 ?
{
x+y=5,
2x-y=1.
交点坐标(2,3)是方程组 的解。
{
x+y=5
2x-y=1
x+y=5
2x-y=1
x=2
y=3
的解
3) 一次函数y=5-x和y=2x-1的图象的交点
坐标(2,3)与方程组 的解有什么关系?
{
x+y=5;
2x-y=1
一般地,从图形的角度看,确定两条直线交点的
坐标,相当于求相应的二元一次方程组的解;解一个二
元一次方程组相当于确定相应两条直线交点的坐标。
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
P(2,2)
y=2x-2
x=2
y=2
所以方程组的解为:
由(2)得 y=2x-2
x=0
y=-2
x=1
y=0
由此可得
进而作出y=2x-2的图象
x=0
y=1
x=-2
y=0
由此可得
解:由(1)得
进而作出 的图象
x-2y=-2 (1)
2x-y=2 (2)
例1:用图象法解二元一次方程组
(1)对应关系
①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③由交点坐标得出方程组的解.
二元一次方程组的解
两个一次函数图象的交点坐标
两个一次函数
(2)图象法解方程组的步骤:
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为
则函数 与 的图象的交点
坐标为 .
(2,2)
3.根据下列图象,你能说出是哪些方程组的解?这些解是什么?
1
1
x
y
0
-2
1
x
y
0
x
3
2
1
-1
-2
y
-2
2
-1
0
1
3
在同一直角坐标系内, 一次函数y = x + 1 和
y = x - 2 的图象有怎样的位置关系?
方程组
解的情况如何?
你发现了什么?
2.方程组 当 时,
方程组无解;反之也成立。
1.两直线
当 平行于 时, ;反之也成立。
求直线 与 直线的交点坐标。你有哪些方法?与同伴交流,并一起分析各种方法的利弊.
解法思路2:由解方程组,得到交点坐标.(把形的问题归结为数的解决,便捷准确)
解法思路l:画出图象找出交点,确定交点坐标近似值.(因作图误差可能有较大差别)
十七世纪法国数学家笛卡尔有一次生病卧床,他看见屋顶上的一只蜘蛛顺着左右爬行,笛卡尔看到蜘蛛的“表演”猛的灵机一动。他想,可以把蜘蛛看成一个点,它可以上、下、左、右运动,能不能知道蜘蛛的位置用一组数确定下来呢?
在蜘蛛爬行的启示下,笛卡尔创建了直角坐
标系,直角坐标系的创建,在代数和几何上架
起了一座桥梁。在坐标系下几何图形(形)
和方程(数)建立了联系。笛卡尔坐标系起
到了桥梁和纽带的作用,而我们可以把图形
化成方程来研究,也可以用图象来研究方程。
这节课我们就来研究二元一次方程(组)
与一次函数(形)的关系。
知识源于悟
益智的“机会”
师:通过以上结论,你能分析研究出二元一次方程与一次函数图象的关系吗?
生:二元一次方程的解就是一次函数图象的点的 坐标;一次函数图象上的点的坐标就是二元一次方程的解.
二元一次方程与一次函数的基本关系
知识的升华
小结 拓展
1) 二元一次方程与一次函数的关系 :
二元一次方程的解是一次函数上点的坐标; 一次函数上每一个点的坐标就是二元一次方程的一组解.
2) 二元一次方程组的解法总共学习了哪几种?
加减法;代入法;图象法.
3) 方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要用代 数方法,进行细致计算.
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
从函数角度解释:
作业
1、习题5.7;
2、相关资料书的习题。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
