北师大版八年级数学上册课件:7.5三角形内角和定理(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册课件:7.5三角形内角和定理(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 818.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:35:19 | ||
图片预览




文档简介
7.5 三角形的内角和定理
向正华
言必有“据”
回顾与思考
?
我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?
1
1
2
A
B
D
2
3
C
(1)如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.如果不实际移动∠A和∠B,那么你还有其它方法可以达到同样的效果?
(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.
“行家”
看“门道”
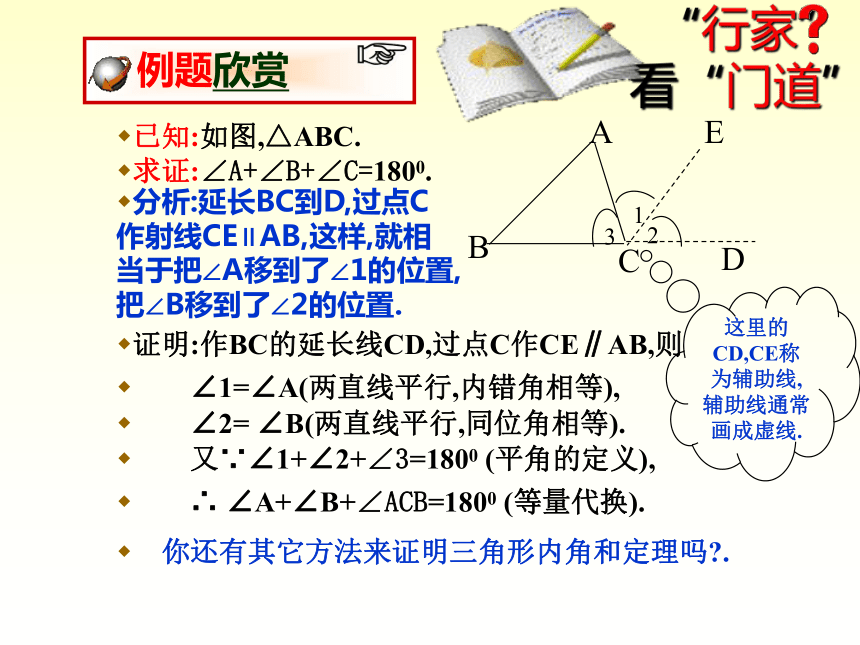
已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
例题欣赏
?
你还有其它方法来证明三角形内角和定理吗?.
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
一题 多解
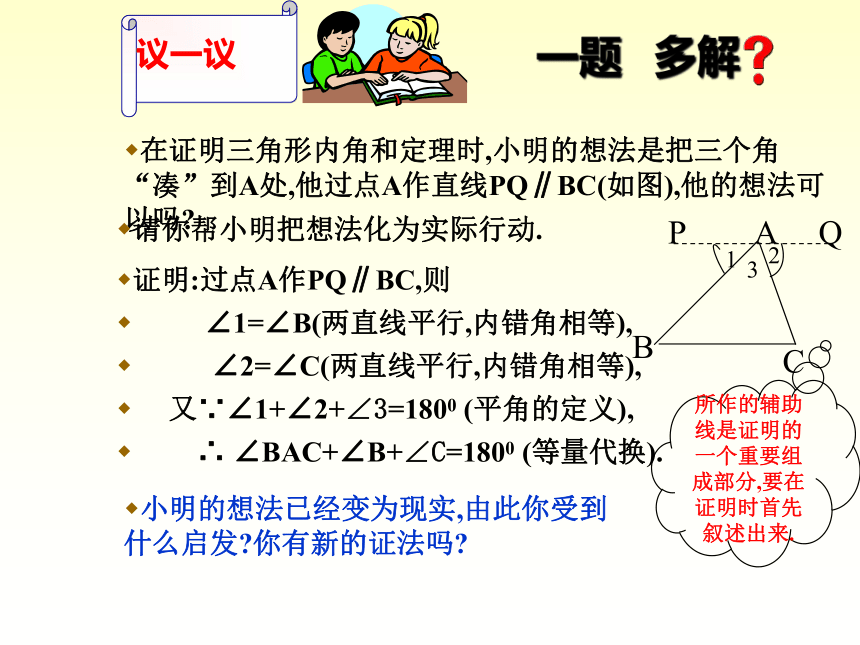
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?
议一议
请你帮小明把想法化为实际行动.
小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?
证明:过点A作PQ∥BC,则
A
B
C
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠BAC+∠B+∠C=1800 (等量代换).
所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.
P
Q
2
3
1
“行家”
看“门道”
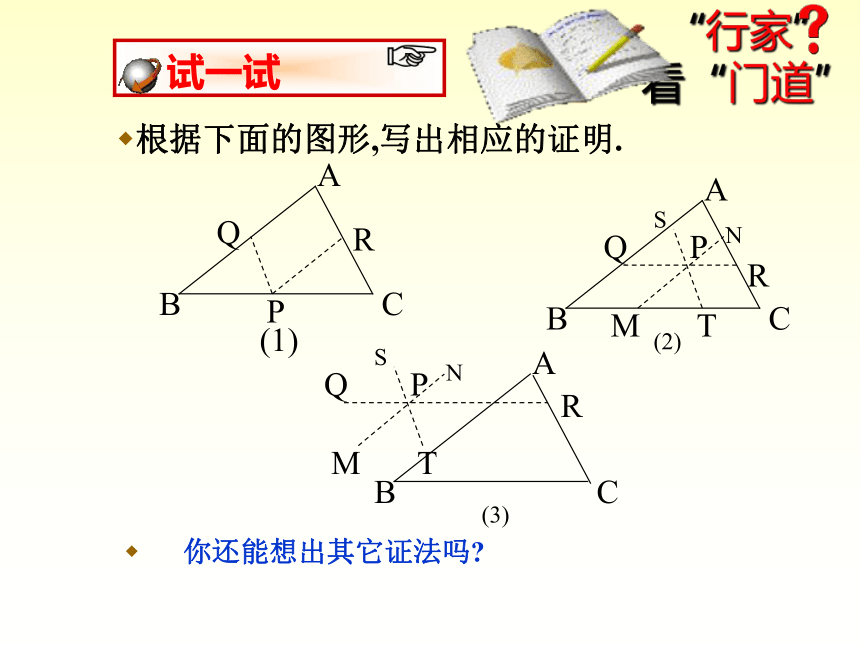
根据下面的图形,写出相应的证明.
试一试
?
你还能想出其它证法吗?
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
例题精讲
A
B
C
D
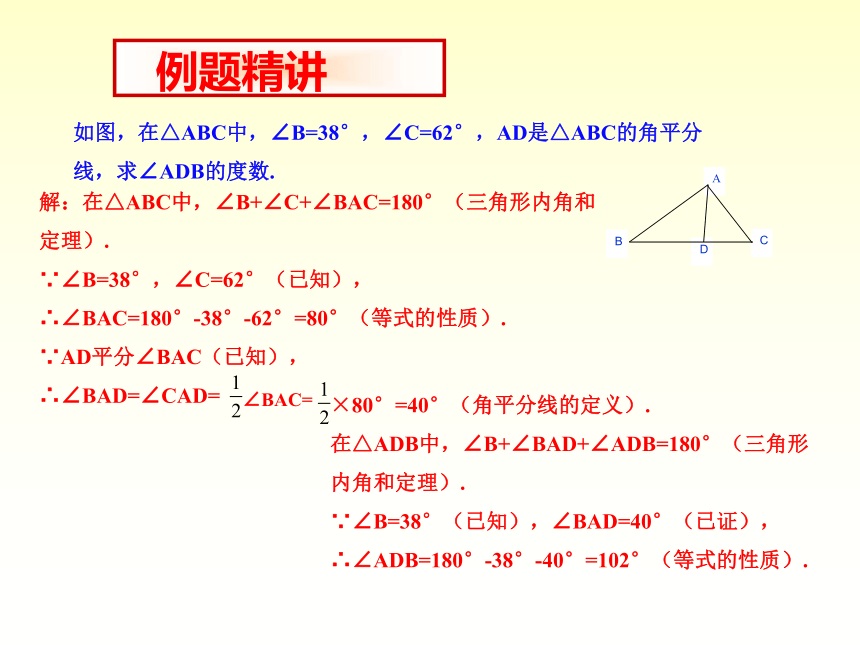
如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数.
解:在△ABC中,∠B+∠C+∠BAC=180°(三角形内角和定理).
∵∠B=38°,∠C=62°(已知),
∴∠BAC=180°-38°-62°=80°(等式的性质).
∵AD平分∠BAC(已知),
∴∠BAD=∠CAD=
∠BAC=
×80°=40°(角平分线的定义).
在△ADB中,∠B+∠BAD+∠ADB=180°(三角形内角和定理).
∵∠B=38°(已知),∠BAD=40°(已证),
∴∠ADB=180°-38°-40°=102°(等式的性质).
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
我是最棒的
1、直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.
2、已知:如图(3),在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500..
随堂练习
?
D
C
B
A
E
A
B
C
A
B
C
结论: 直角三角形的两个锐角互余.以后可以直接运用.
(1)
(2)
(3)
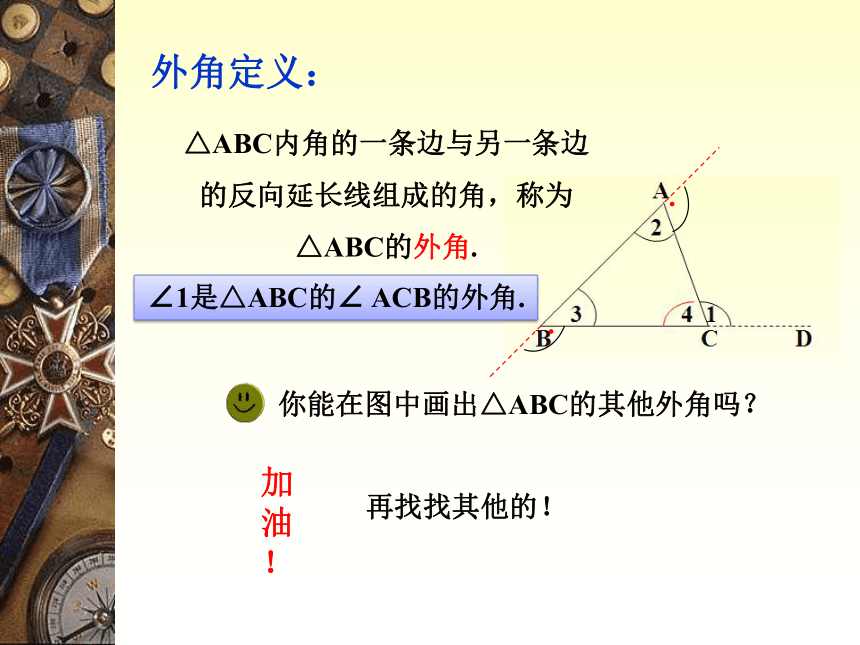
外角定义:
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
∠1是△ABC的∠ ACB的外角.
你能在图中画出△ABC的其他外角吗?
.
.
加油
!
再找找其他的!
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系?
∠1+∠4=1800 ;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗?
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证明.
还有其它方法吗?
方法一
A
C
D
B
E
·
·
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证明.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
方法二
A
C
D
B
E
·
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =1800 (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =1800 (等量代换).
∴ AD∥BC(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证明.
证明:由证法1可得:
·
方法三
例 已知:如图,P 是△ABC内一点,链接PB,PC.
求证: ∠ BPC > ∠A.
A
B
C
D
P
证明:如图,延长BP,交AC于点D.
∵ ∠ BPC是△PDC的一个外角(外角的定义)
∴ ∠ BPC > ∠ PDC
(三角形的一个外角大于任何一个和它不相邻的内角)
∵ ∠ PDC是△ABD的一个外角(外角的定义)
∴ ∠ PDC > ∠ A
(三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠ BPC > ∠ A
你还有其他的
证明方法吗?
例3 已知:如图6-14,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
∴ ∠1>∠3(三角形的一个外角大于任何一个和 它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任 何一个和 它不相邻的内角).
∴ ∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(1):延长BD与AC相交于E
∵ ∠BDC是△DCE的一个外角 (外角定义),
∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠BDC>∠A (不等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角定义),
B
C
A
D
E
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(2):∵ ∠BDC是△DCE的一个外角 (外角定义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角定义),
B
C
A
D
E
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的定义),
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
又∵ ∠2是△EHC的一个外角(外角的定义),
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
三角形内角和定理 :
三角形三个内角的和等于1800。
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
推论3:
直角三角形的两锐角互余.
作业
1、习题7.6;习题7.7;
2、相关资料书的习题。
向正华
言必有“据”
回顾与思考
?
我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?
1
1
2
A
B
D
2
3
C
(1)如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.如果不实际移动∠A和∠B,那么你还有其它方法可以达到同样的效果?
(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.
“行家”
看“门道”
已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
例题欣赏
?
你还有其它方法来证明三角形内角和定理吗?.
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
一题 多解
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?
议一议
请你帮小明把想法化为实际行动.
小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?
证明:过点A作PQ∥BC,则
A
B
C
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠BAC+∠B+∠C=1800 (等量代换).
所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.
P
Q
2
3
1
“行家”
看“门道”
根据下面的图形,写出相应的证明.
试一试
?
你还能想出其它证法吗?
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
例题精讲
A
B
C
D
如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数.
解:在△ABC中,∠B+∠C+∠BAC=180°(三角形内角和定理).
∵∠B=38°,∠C=62°(已知),
∴∠BAC=180°-38°-62°=80°(等式的性质).
∵AD平分∠BAC(已知),
∴∠BAD=∠CAD=
∠BAC=
×80°=40°(角平分线的定义).
在△ADB中,∠B+∠BAD+∠ADB=180°(三角形内角和定理).
∵∠B=38°(已知),∠BAD=40°(已证),
∴∠ADB=180°-38°-40°=102°(等式的性质).
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
我是最棒的
1、直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.
2、已知:如图(3),在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500..
随堂练习
?
D
C
B
A
E
A
B
C
A
B
C
结论: 直角三角形的两个锐角互余.以后可以直接运用.
(1)
(2)
(3)
外角定义:
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
∠1是△ABC的∠ ACB的外角.
你能在图中画出△ABC的其他外角吗?
.
.
加油
!
再找找其他的!
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系?
∠1+∠4=1800 ;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗?
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证明.
还有其它方法吗?
方法一
A
C
D
B
E
·
·
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证明.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
方法二
A
C
D
B
E
·
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =1800 (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =1800 (等量代换).
∴ AD∥BC(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证明.
证明:由证法1可得:
·
方法三
例 已知:如图,P 是△ABC内一点,链接PB,PC.
求证: ∠ BPC > ∠A.
A
B
C
D
P
证明:如图,延长BP,交AC于点D.
∵ ∠ BPC是△PDC的一个外角(外角的定义)
∴ ∠ BPC > ∠ PDC
(三角形的一个外角大于任何一个和它不相邻的内角)
∵ ∠ PDC是△ABD的一个外角(外角的定义)
∴ ∠ PDC > ∠ A
(三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠ BPC > ∠ A
你还有其他的
证明方法吗?
例3 已知:如图6-14,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
∴ ∠1>∠3(三角形的一个外角大于任何一个和 它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任 何一个和 它不相邻的内角).
∴ ∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(1):延长BD与AC相交于E
∵ ∠BDC是△DCE的一个外角 (外角定义),
∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠BDC>∠A (不等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角定义),
B
C
A
D
E
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(2):∵ ∠BDC是△DCE的一个外角 (外角定义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角定义),
B
C
A
D
E
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的定义),
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
又∵ ∠2是△EHC的一个外角(外角的定义),
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
三角形内角和定理 :
三角形三个内角的和等于1800。
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
推论3:
直角三角形的两锐角互余.
作业
1、习题7.6;习题7.7;
2、相关资料书的习题。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
