北师大版九年级数学下册教学课件:1.6 利用三角函数测高(共19张PPT)
文档属性
| 名称 | 北师大版九年级数学下册教学课件:1.6 利用三角函数测高(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览




文档简介
1.6 利用三角函数测高
课程讲授
新知导入
随堂练习
课堂小结
第一章 直角三角形的边角关系
知识要点
1.测量底部可以到达的物体的高度
2.测量底部不可以到达的物体的高度
新知导入
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
哈利法塔原名迪拜塔,又称迪拜大厦或比斯迪拜塔,塔高828米,楼层总数162层。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米,
新知导入
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
天津117大厦结构高度达596.5米
平安国际金融中心项目建筑核心筒结构高度592.5米,建成后总高度为592.5米。
课程讲授
1
测量底部可以到达的物体的高度
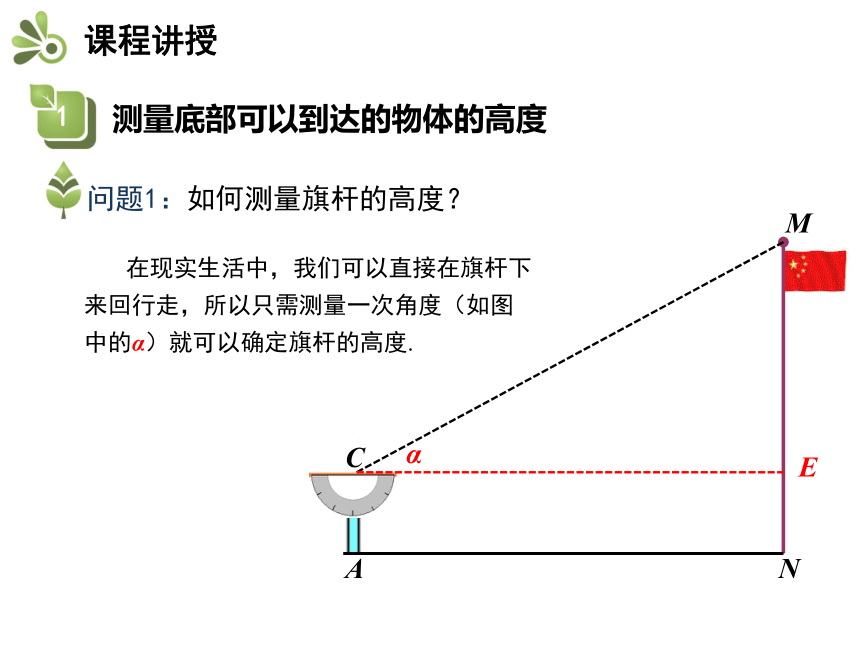
问题1:如何测量旗杆的高度?
A
C
M
N
E
α
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.
课程讲授
1
测量底部可以到达的物体的高度
问题1:如何测量旗杆的高度?
A
C
M
N
E
α
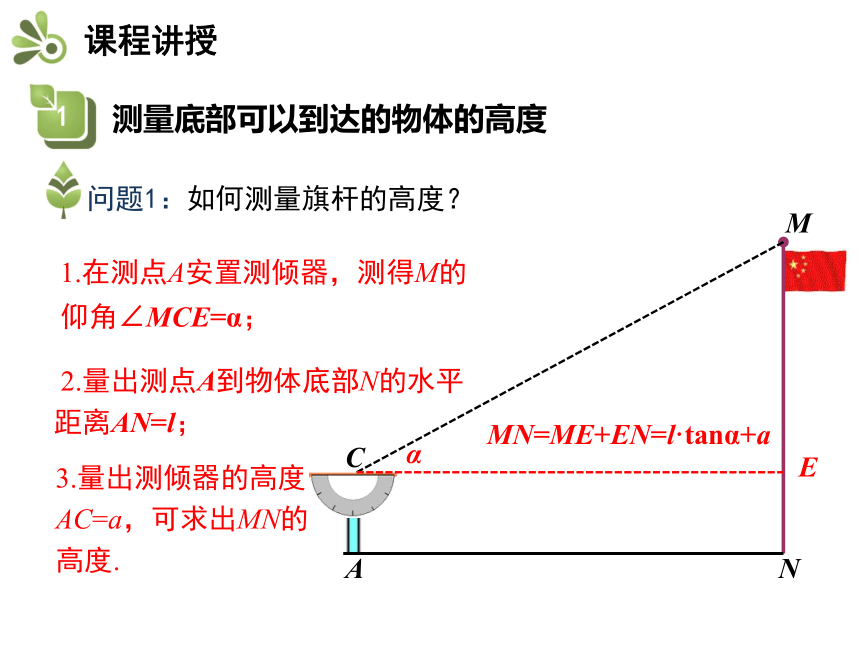
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
课程讲授
1
测量底部可以到达的物体的高度
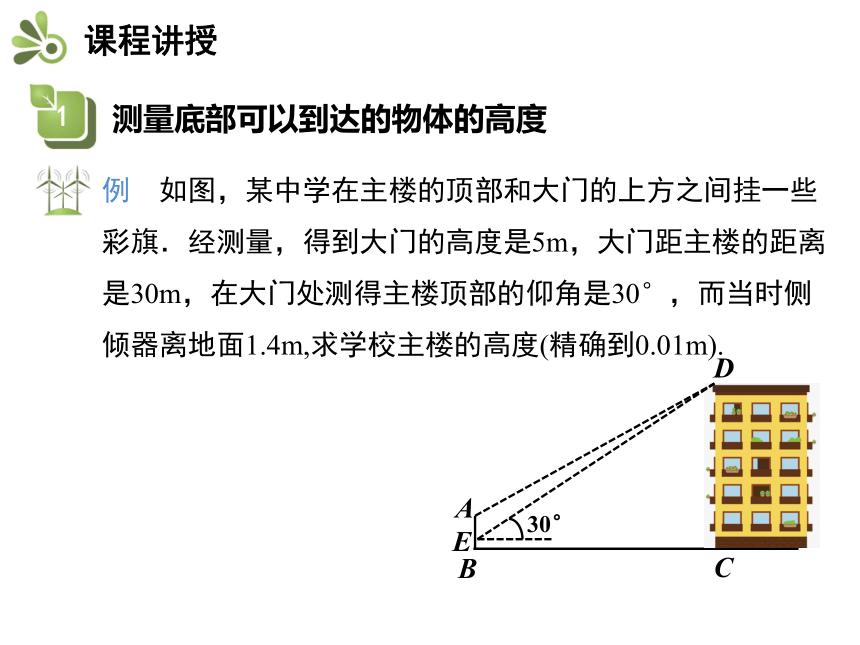
例 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
课程讲授
1
测量底部可以到达的物体的高度
C
A
B
E
D
30°
解 如图,作EM垂直CD于M点,
∠DEM=30°,
M
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
课程讲授
1
测量底部可以到达的物体的高度
练一练:如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12 m,则大厅两层之间的高度为___________m.(结果保留两位小数,参考数据:sin31°≈0.515,cos31°≈0.857,tan31°≈0.601)
6.18
课程讲授
2
测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
M
A
C
B
D
N
E
α
β
在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.
课程讲授
2
测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
M
A
C
B
D
N
E
α
β
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
课程讲授
2
测量底部不可以到达的物体的高度
练一练:如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
A
随堂练习
1.如图,两建筑物的水平距离BC为18 m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°,则建筑物CD的高度为___________m.(结果保留根号)
随堂练习
5.4
2.如图,一幢大楼的顶部竖有一块写有校训的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度约为_________米.(测倾器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)
3.在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动.如图,在测点A处安置测倾器,量出高度AB=1.5 m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20 m,根据测量数据,求旗杆CD的高度.(结果精确到0.1 m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
随堂练习
随堂练习
答:旗杆CD的高度约13.9米.
解:由题意得AC=20米,
AB=1.5米,
∵∠DBE=32°,
∴DE=BE·tan32°≈20×0.62=12.4(米),
∴CD=DE+CE=DE+AB=12.4+1.5=13.9(米).
随堂练习
4.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)
A
B
C
D
E
39°
45°
随堂练习
A
B
C
D
E
39°
45°
解:(1)由题意,AC=AB=610(米);
(2)DE=AC=610(米),
在Rt△BDE中,tan∠BDE=
BE
DE
=610-610×tan39°≈116(米)
故BE=DEtan39°.
因为CD=AE,
所以CD=AB-DE·tan39°
课堂小结
利用三角函数测高
测量底部可以到达的物体的高度
测量底部不可以到达的物体的高度
课程讲授
新知导入
随堂练习
课堂小结
第一章 直角三角形的边角关系
知识要点
1.测量底部可以到达的物体的高度
2.测量底部不可以到达的物体的高度
新知导入
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
哈利法塔原名迪拜塔,又称迪拜大厦或比斯迪拜塔,塔高828米,楼层总数162层。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米,
新知导入
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
天津117大厦结构高度达596.5米
平安国际金融中心项目建筑核心筒结构高度592.5米,建成后总高度为592.5米。
课程讲授
1
测量底部可以到达的物体的高度
问题1:如何测量旗杆的高度?
A
C
M
N
E
α
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.
课程讲授
1
测量底部可以到达的物体的高度
问题1:如何测量旗杆的高度?
A
C
M
N
E
α
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
课程讲授
1
测量底部可以到达的物体的高度
例 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
课程讲授
1
测量底部可以到达的物体的高度
C
A
B
E
D
30°
解 如图,作EM垂直CD于M点,
∠DEM=30°,
M
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
课程讲授
1
测量底部可以到达的物体的高度
练一练:如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12 m,则大厅两层之间的高度为___________m.(结果保留两位小数,参考数据:sin31°≈0.515,cos31°≈0.857,tan31°≈0.601)
6.18
课程讲授
2
测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
M
A
C
B
D
N
E
α
β
在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.
课程讲授
2
测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
M
A
C
B
D
N
E
α
β
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
课程讲授
2
测量底部不可以到达的物体的高度
练一练:如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
A
随堂练习
1.如图,两建筑物的水平距离BC为18 m,从点A测得点D的俯角α为30°,测得点C的俯角β为60°,则建筑物CD的高度为___________m.(结果保留根号)
随堂练习
5.4
2.如图,一幢大楼的顶部竖有一块写有校训的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度约为_________米.(测倾器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.414, ≈1.732)
3.在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动.如图,在测点A处安置测倾器,量出高度AB=1.5 m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20 m,根据测量数据,求旗杆CD的高度.(结果精确到0.1 m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
随堂练习
随堂练习
答:旗杆CD的高度约13.9米.
解:由题意得AC=20米,
AB=1.5米,
∵∠DBE=32°,
∴DE=BE·tan32°≈20×0.62=12.4(米),
∴CD=DE+CE=DE+AB=12.4+1.5=13.9(米).
随堂练习
4.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)
A
B
C
D
E
39°
45°
随堂练习
A
B
C
D
E
39°
45°
解:(1)由题意,AC=AB=610(米);
(2)DE=AC=610(米),
在Rt△BDE中,tan∠BDE=
BE
DE
=610-610×tan39°≈116(米)
故BE=DEtan39°.
因为CD=AE,
所以CD=AB-DE·tan39°
课堂小结
利用三角函数测高
测量底部可以到达的物体的高度
测量底部不可以到达的物体的高度
