北师大版九年级数学下册教学课件:3.7 切线长定理(共16张PPT)
文档属性
| 名称 | 北师大版九年级数学下册教学课件:3.7 切线长定理(共16张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:41:37 | ||
图片预览


文档简介
课程讲授
新知导入
随堂练习
课堂小结
3.7 切线长定理
第三章 圆
知识要点
1.切线长定理
新知导入
看一看:观察下图中图形运动,试着发现其中的规律。
课程讲授
1
切线长定理
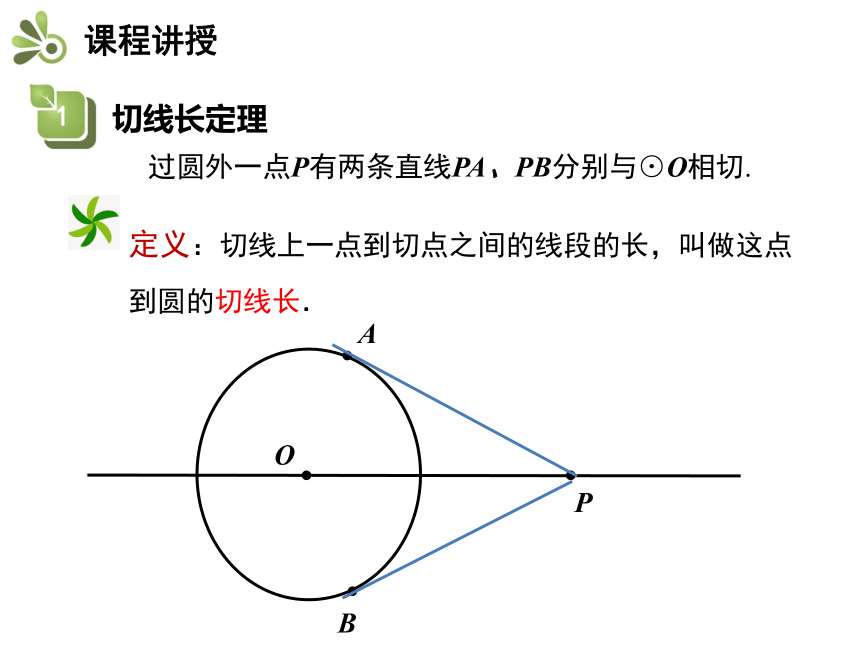
过圆外一点P有两条直线PA、PB分别与⊙O相切.
定义:切线上一点到切点之间的线段的长,叫做这点到圆的切线长.
O
P
A
B
课程讲授
1
切线长定理
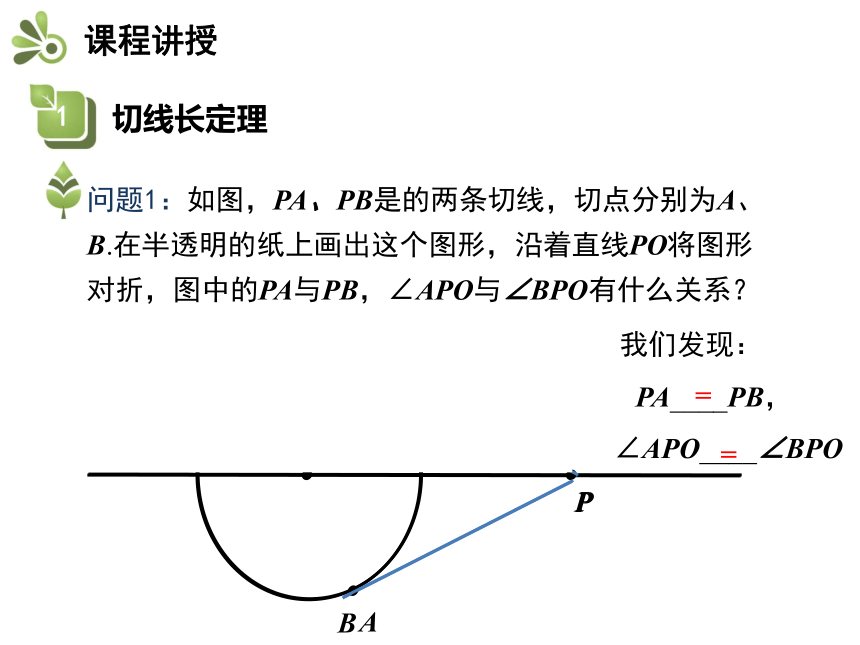
问题1:如图,PA、PB是的两条切线,切点分别为A、B.在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
O
P
A
B
O
P
A
A
我们发现:
PA____PB,
∠APO____∠BPO
=
=
课程讲授
1
切线长定理
O
P
A
B
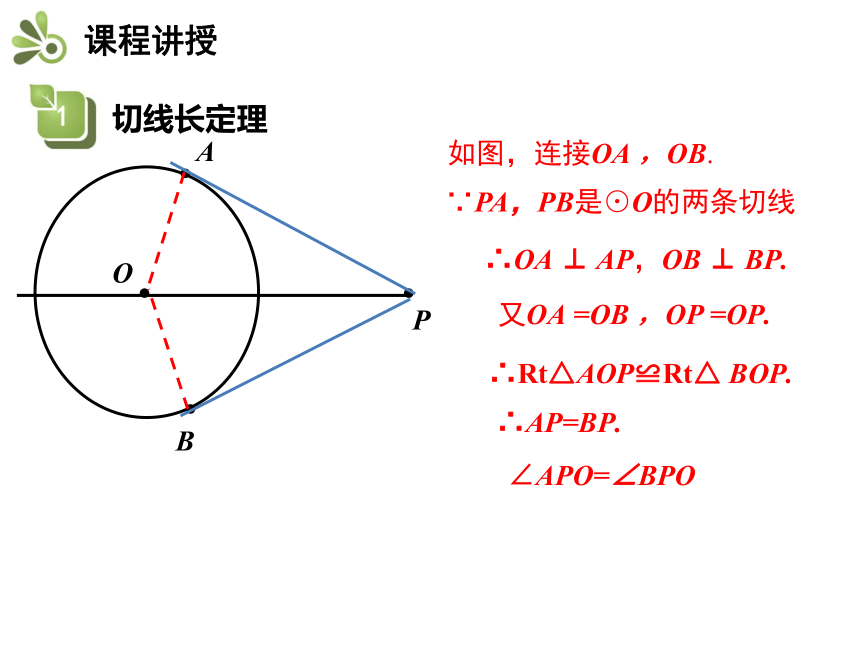
如图,连接OA ,OB.
∵PA,PB是⊙O的两条切线
∴OA ⊥ AP,OB ⊥ BP.
又OA =OB ,OP =OP.
∴Rt△AOP≌Rt△ BOP.
∴AP=BP.
∠APO=∠BPO
课程讲授
1
切线长定理
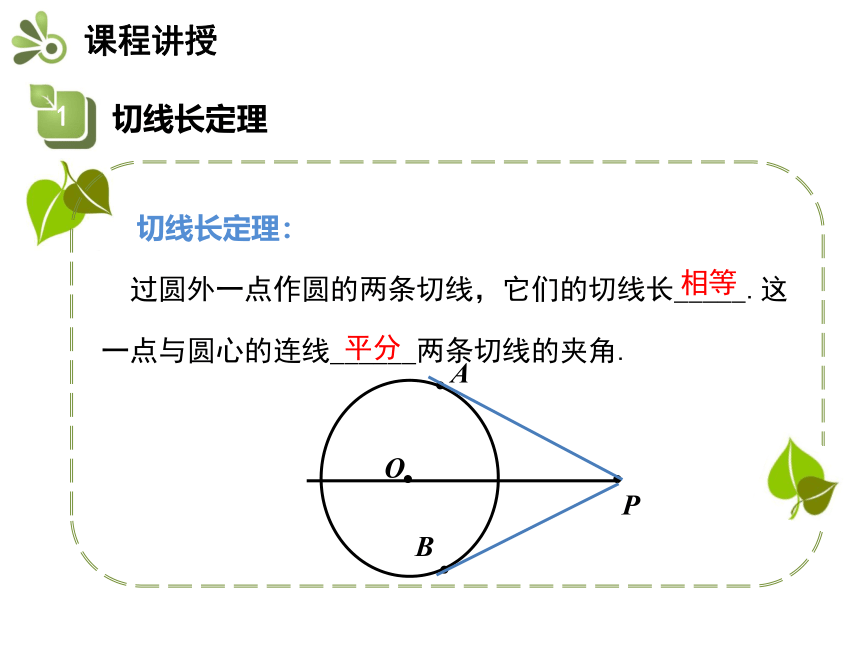
切线长定理:
过圆外一点作圆的两条切线,它们的切线长_____.这一点与圆心的连线______两条切线的夹角.
相等
平分
O
P
A
B
课程讲授
1
切线长定理
练一练:如图,PA,PB为⊙O的切线,A,B为切点,根据图形得出四个结论:
①PA=PB;
②∠1=∠2;
③∠3=∠4;
④AB被OP垂直平分.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
D
随堂练习
1.如图,PA,PB是⊙O的切线,点A,B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.40° B.60° C.70° D.80°
C
随堂练习
2.如图,一圆内切于四边形ABCD,切点分别为E,F,G,H,且AB=16,CD=10,则四边形的周长为( )
A.50
B.52
C.54
D.56
B
随堂练习
3.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56 ° B.62° C.68° D.78°
C
随堂练习
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?( )
A.3步
B.5步
C.6步
D.8步
C
随堂练习
5.如图,P是⊙O外一点,PA,PB分别与⊙O切于A,B两点,PA=4 cm,∠APB=40°,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于点D,E.求:
(1)△PDE的周长;
(2)∠DOE的度数.
)
随堂练习
=PA+PB
解 (1)∵PA,PB分别切⊙O于点A,B,
∴PB=PA=4 cm.
同理可得DA=DC,EC=EB.
∵△PDE的周长=PD+PE+DE,
DE=DC+CE,
∴△PDE的周长
=(PD+DA)+(PE+EB)
=8 cm.
随堂练习
解 (2)连接OC.
∵DA,DC分别切⊙O于点A,C,
∴∠AOD=∠DOC.
同理可得∠COE=∠BOE.
∵∠DOE=∠AOD+∠COE,
∵PA,PB分别切⊙O于点A,B,
∴∠DOE= ∠AOB.
2
1
∴∠DOE= ∠AOB=70°.
2
1
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°.
∵四边形内角和为360°,
=360°-∠PAO-∠PBO-∠APB
=140°,
∴∠AOB
课堂小结
切线长定理
过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角.
新知导入
随堂练习
课堂小结
3.7 切线长定理
第三章 圆
知识要点
1.切线长定理
新知导入
看一看:观察下图中图形运动,试着发现其中的规律。
课程讲授
1
切线长定理
过圆外一点P有两条直线PA、PB分别与⊙O相切.
定义:切线上一点到切点之间的线段的长,叫做这点到圆的切线长.
O
P
A
B
课程讲授
1
切线长定理
问题1:如图,PA、PB是的两条切线,切点分别为A、B.在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
O
P
A
B
O
P
A
A
我们发现:
PA____PB,
∠APO____∠BPO
=
=
课程讲授
1
切线长定理
O
P
A
B
如图,连接OA ,OB.
∵PA,PB是⊙O的两条切线
∴OA ⊥ AP,OB ⊥ BP.
又OA =OB ,OP =OP.
∴Rt△AOP≌Rt△ BOP.
∴AP=BP.
∠APO=∠BPO
课程讲授
1
切线长定理
切线长定理:
过圆外一点作圆的两条切线,它们的切线长_____.这一点与圆心的连线______两条切线的夹角.
相等
平分
O
P
A
B
课程讲授
1
切线长定理
练一练:如图,PA,PB为⊙O的切线,A,B为切点,根据图形得出四个结论:
①PA=PB;
②∠1=∠2;
③∠3=∠4;
④AB被OP垂直平分.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
D
随堂练习
1.如图,PA,PB是⊙O的切线,点A,B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.40° B.60° C.70° D.80°
C
随堂练习
2.如图,一圆内切于四边形ABCD,切点分别为E,F,G,H,且AB=16,CD=10,则四边形的周长为( )
A.50
B.52
C.54
D.56
B
随堂练习
3.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56 ° B.62° C.68° D.78°
C
随堂练习
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?( )
A.3步
B.5步
C.6步
D.8步
C
随堂练习
5.如图,P是⊙O外一点,PA,PB分别与⊙O切于A,B两点,PA=4 cm,∠APB=40°,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于点D,E.求:
(1)△PDE的周长;
(2)∠DOE的度数.
)
随堂练习
=PA+PB
解 (1)∵PA,PB分别切⊙O于点A,B,
∴PB=PA=4 cm.
同理可得DA=DC,EC=EB.
∵△PDE的周长=PD+PE+DE,
DE=DC+CE,
∴△PDE的周长
=(PD+DA)+(PE+EB)
=8 cm.
随堂练习
解 (2)连接OC.
∵DA,DC分别切⊙O于点A,C,
∴∠AOD=∠DOC.
同理可得∠COE=∠BOE.
∵∠DOE=∠AOD+∠COE,
∵PA,PB分别切⊙O于点A,B,
∴∠DOE= ∠AOB.
2
1
∴∠DOE= ∠AOB=70°.
2
1
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°.
∵四边形内角和为360°,
=360°-∠PAO-∠PBO-∠APB
=140°,
∴∠AOB
课堂小结
切线长定理
过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角.
