北师大版九年级数学下册教学课件:3.9 弧长及扇形的面积(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下册教学课件:3.9 弧长及扇形的面积(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:40:56 | ||
图片预览






文档简介
3.9 弧长及扇形的面积
课程讲授
新知导入
随堂练习
课堂小结
第三章 圆
知识要点
1.弧长公式及应用
2.扇形面积公式及应用
新知导入
看一看:观察下图中图形,试着发现它们的规律。
新知导入
看一看:观察下图中图形,试着发现它们的规律。
课程讲授
1
弧长公式及应用
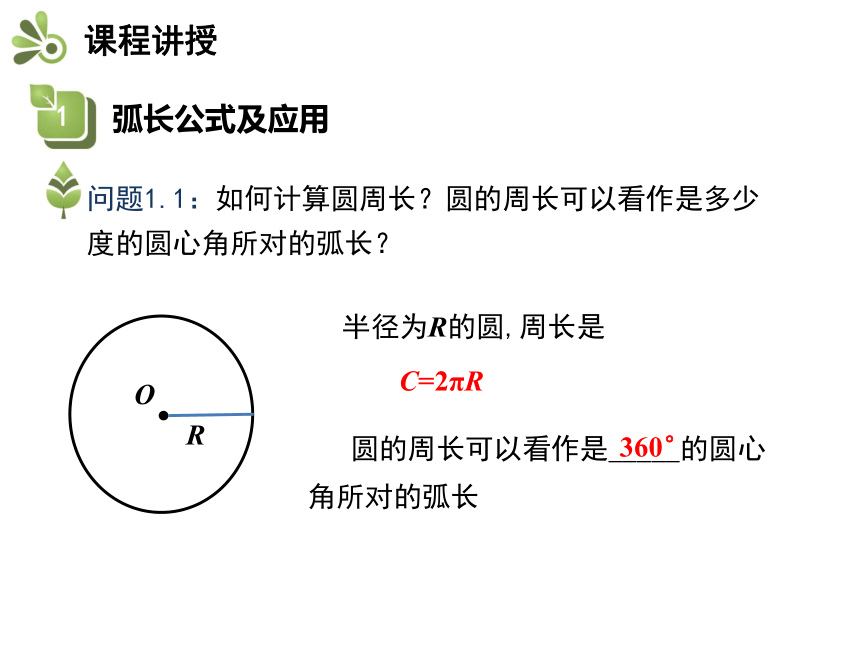
问题1.1:如何计算圆周长?圆的周长可以看作是多少度的圆心角所对的弧长?
O
R
半径为R的圆,周长是
C=2πR
圆的周长可以看作是_____的圆心角所对的弧长
360°
课程讲授
1
弧长公式及应用
问题1.2:1°的圆心角所对的弧长是多少?n°的圆心角所对的弧长是多少?
O
90°
O
180°
O
270°
O
课程讲授
1
弧长公式及应用
O
n°
R
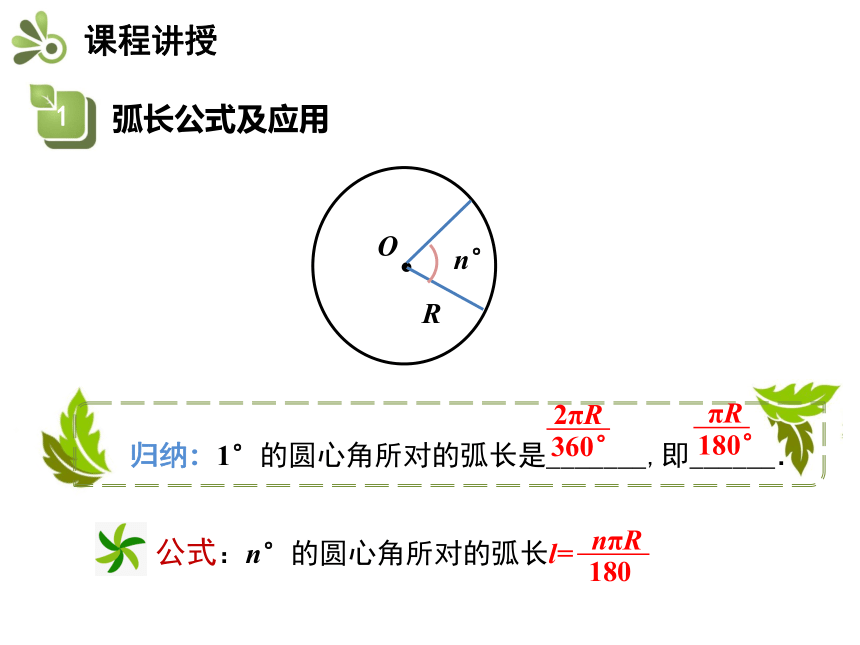
归纳:1°的圆心角所对的弧长是_______,即______.
2πR
360°
πR
180°
公式:n°的圆心角所对的弧长l=
nπR
180
课程讲授
1
弧长公式及应用
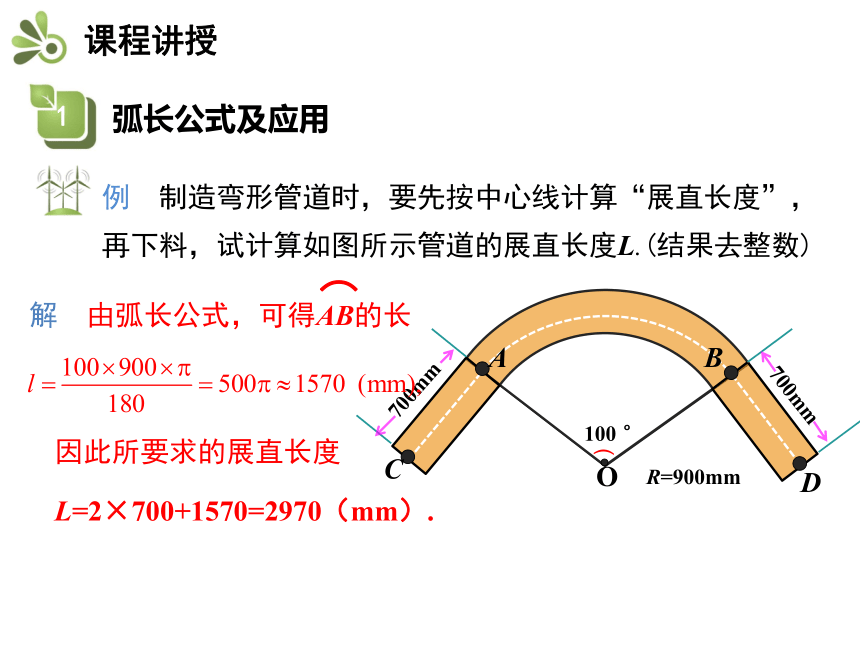
例 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.(结果去整数)
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
解 由弧长公式,可得AB的长
)
L=2×700+1570=2970(mm).
因此所要求的展直长度
课程讲授
1
弧长公式及应用
练一练:已知扇形的圆心角为60°,半径为1,则扇形的弧长为( )
A.
B.π
C.
D.
D
课程讲授
2
扇形面积公式及应用
O
定义:由圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
可以发现:扇形的面积除了与圆的半径有关还与组成扇形的_______的大小有关.
圆心角
课程讲授
问题1.1:如何计算圆的面积?圆的面积可以看作是多少度的圆心角所对扇形的面积?
O
R
半径为R的圆,面积是
S=πR2
圆的面积可以看作是_____的圆心角所对的扇形面积.
360°
2
扇形面积公式及应用
课程讲授
2
扇形面积公式及应用
问题1.2:1°的圆心角所对的扇形面积是多少?n°的圆心角所对的扇形面积是多少?
O
90°
O
180°
O
270°
O
课程讲授
O
n°
R
归纳:1°的圆心角所对的扇形面积是_____.
πR2
360
公式:n°的圆心角所对的扇形面积S扇形=
nπR2
360
对比弧长公式可以得到
S扇形= lR
2
1
2
扇形面积公式及应用
例 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积.(结果保留小数点后两位)
2
扇形面积公式及应用
课程讲授
O
解 如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
B
A
D
C
∵ OC=0.6m, DC=0.3m,
∴ OD=OC- DC=0.3(m),
∴ OD=DC.
课程讲授
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
O
B
A
D
C
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - SΔOAB
2
扇形面积公式及应用
课程讲授
练一练:在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是( )
A.6π cm2
B.8π cm2
C.12π cm2
D.24π cm2
C
2
扇形面积公式及应用
随堂练习
1.圆心角为120°,弧长为12π的扇形的半径为( )
A.6 B.9
C.18 D.36
2.一个扇形的半径为8 cm,弧长为 cm,则扇形的圆心角为( )
A.60°
B.120°
C.150°
D.180°
C
B
随堂练习
3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点 C逆时针旋转60°得到△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
B
随堂练习
4.一个扇形的圆心角是120°,面积是3π cm2,那么这个扇形的半径是( )
A.1 cm B.3 cm
C.6 cm D.9 cm
B
5.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( )
A.π B.2π
C.3π D.5π
)
B
随堂练习
6.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是点A,B,C,如果AB=1,求曲线CDEF的长.
解 ∵△ABC是正三角形,AB=1,
∴∠CAD=∠DBE=∠ECF=120°,
AC=AD=1,BD=BE=2,CE=CF=3,
∴l弧CD=120×π×1÷180= π,
3
2
3
4
l弧ED=120×π×2÷180= π,
l弧EF=120×π×3÷180=2π,
∴曲线CDEF的长为 π+ π+2π=4π.
3
2
3
4
随堂练习
7.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
解 (1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
= π·52- ×5×5
360
90
2
1
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
课堂小结
弧长及扇形面积
弧长公式及应用
扇形面积公式及应用
n°的圆心角所对的弧长l=
nπR
180
n°的圆心角所对的扇形面积S扇形=
nπR2
360
课程讲授
新知导入
随堂练习
课堂小结
第三章 圆
知识要点
1.弧长公式及应用
2.扇形面积公式及应用
新知导入
看一看:观察下图中图形,试着发现它们的规律。
新知导入
看一看:观察下图中图形,试着发现它们的规律。
课程讲授
1
弧长公式及应用
问题1.1:如何计算圆周长?圆的周长可以看作是多少度的圆心角所对的弧长?
O
R
半径为R的圆,周长是
C=2πR
圆的周长可以看作是_____的圆心角所对的弧长
360°
课程讲授
1
弧长公式及应用
问题1.2:1°的圆心角所对的弧长是多少?n°的圆心角所对的弧长是多少?
O
90°
O
180°
O
270°
O
课程讲授
1
弧长公式及应用
O
n°
R
归纳:1°的圆心角所对的弧长是_______,即______.
2πR
360°
πR
180°
公式:n°的圆心角所对的弧长l=
nπR
180
课程讲授
1
弧长公式及应用
例 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.(结果去整数)
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
解 由弧长公式,可得AB的长
)
L=2×700+1570=2970(mm).
因此所要求的展直长度
课程讲授
1
弧长公式及应用
练一练:已知扇形的圆心角为60°,半径为1,则扇形的弧长为( )
A.
B.π
C.
D.
D
课程讲授
2
扇形面积公式及应用
O
定义:由圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
可以发现:扇形的面积除了与圆的半径有关还与组成扇形的_______的大小有关.
圆心角
课程讲授
问题1.1:如何计算圆的面积?圆的面积可以看作是多少度的圆心角所对扇形的面积?
O
R
半径为R的圆,面积是
S=πR2
圆的面积可以看作是_____的圆心角所对的扇形面积.
360°
2
扇形面积公式及应用
课程讲授
2
扇形面积公式及应用
问题1.2:1°的圆心角所对的扇形面积是多少?n°的圆心角所对的扇形面积是多少?
O
90°
O
180°
O
270°
O
课程讲授
O
n°
R
归纳:1°的圆心角所对的扇形面积是_____.
πR2
360
公式:n°的圆心角所对的扇形面积S扇形=
nπR2
360
对比弧长公式可以得到
S扇形= lR
2
1
2
扇形面积公式及应用
例 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积.(结果保留小数点后两位)
2
扇形面积公式及应用
课程讲授
O
解 如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
B
A
D
C
∵ OC=0.6m, DC=0.3m,
∴ OD=OC- DC=0.3(m),
∴ OD=DC.
课程讲授
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
O
B
A
D
C
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - SΔOAB
2
扇形面积公式及应用
课程讲授
练一练:在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是( )
A.6π cm2
B.8π cm2
C.12π cm2
D.24π cm2
C
2
扇形面积公式及应用
随堂练习
1.圆心角为120°,弧长为12π的扇形的半径为( )
A.6 B.9
C.18 D.36
2.一个扇形的半径为8 cm,弧长为 cm,则扇形的圆心角为( )
A.60°
B.120°
C.150°
D.180°
C
B
随堂练习
3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点 C逆时针旋转60°得到△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
B
随堂练习
4.一个扇形的圆心角是120°,面积是3π cm2,那么这个扇形的半径是( )
A.1 cm B.3 cm
C.6 cm D.9 cm
B
5.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( )
A.π B.2π
C.3π D.5π
)
B
随堂练习
6.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是点A,B,C,如果AB=1,求曲线CDEF的长.
解 ∵△ABC是正三角形,AB=1,
∴∠CAD=∠DBE=∠ECF=120°,
AC=AD=1,BD=BE=2,CE=CF=3,
∴l弧CD=120×π×1÷180= π,
3
2
3
4
l弧ED=120×π×2÷180= π,
l弧EF=120×π×3÷180=2π,
∴曲线CDEF的长为 π+ π+2π=4π.
3
2
3
4
随堂练习
7.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
解 (1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
= π·52- ×5×5
360
90
2
1
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
课堂小结
弧长及扇形面积
弧长公式及应用
扇形面积公式及应用
n°的圆心角所对的弧长l=
nπR
180
n°的圆心角所对的扇形面积S扇形=
nπR2
360
