北师大版九年级数学下册课件:1.2 30°,45°,60°角的三角函数值(一课时) (共18张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:1.2 30°,45°,60°角的三角函数值(一课时) (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 463.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:39:15 | ||
图片预览






文档简介
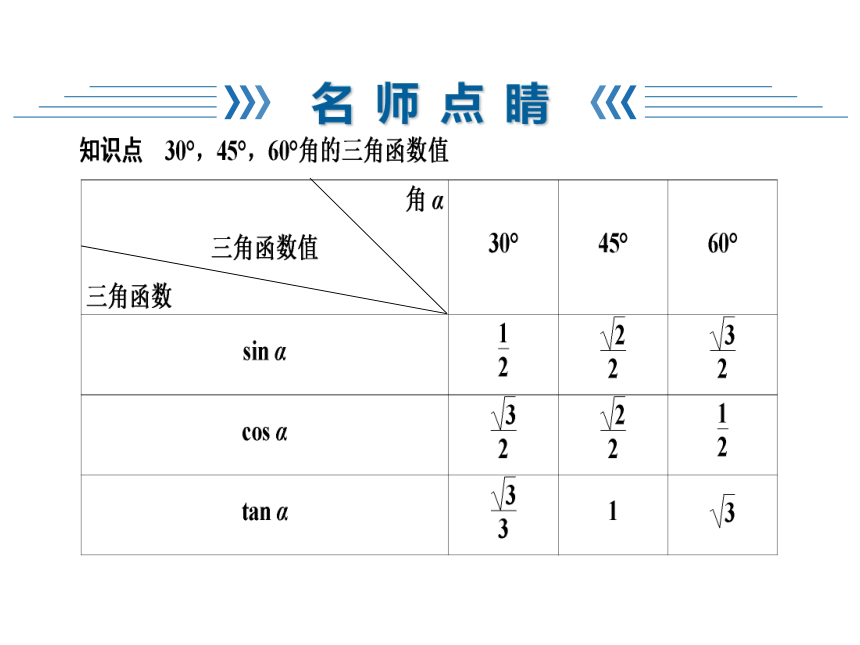
由上表可知:(1)任意一个锐角的正(余)弦值,等于它的余角的余(正)弦值.(2)锐角的正切值总比正弦值大.
拓展:当0°<α<45°时,sin α<cos α;
当α=45°时,sin α=cos α;
当45°<α<90°时,sin α>cos α.
分析:根据特殊角的三角函数值计算、求解.
6.计算:
(1)sin2 60°+cos2 60°-tan 45°;
11.已知对任意锐角α、β均有:cos(α+β)=cos α·cos β-sin α·sin β,则cos 75°=__________.
12.如图,正方形ABCD与正方形BEFC全等,则tan(∠BAF+∠AFB)=________.
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长.
15.如图,在四边形ABCD中,∠BAD=60°,∠B=∠D=90°,BC=11,CD=2,求对角线AC的长.
16.对于钝角α,定义它的三角函数值如下:
sin α=sin(180°-α),cos α=-cos(180°-α).
(1)求sin 120°、cos 120°、sin 150°的值;
(2)若一个三角形的三个内角的比是1∶1∶4,A、B是这个三角形的两个顶点,sin A、cos B是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
第一章 直角三角形的边角关系
2 30°,45°,60°角的三角函数值(一课时)
基础过关
名师点睛
能力提升
以练助学
思维训练
名 师 点 睛
基 础 过 关
C
A
C
90°
解:原式=1-tan 30°+tan 30°=1.
能 力 提 升
B
A
B
1
思 维 训 练
拓展:当0°<α<45°时,sin α<cos α;
当α=45°时,sin α=cos α;
当45°<α<90°时,sin α>cos α.
分析:根据特殊角的三角函数值计算、求解.
6.计算:
(1)sin2 60°+cos2 60°-tan 45°;
11.已知对任意锐角α、β均有:cos(α+β)=cos α·cos β-sin α·sin β,则cos 75°=__________.
12.如图,正方形ABCD与正方形BEFC全等,则tan(∠BAF+∠AFB)=________.
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长.
15.如图,在四边形ABCD中,∠BAD=60°,∠B=∠D=90°,BC=11,CD=2,求对角线AC的长.
16.对于钝角α,定义它的三角函数值如下:
sin α=sin(180°-α),cos α=-cos(180°-α).
(1)求sin 120°、cos 120°、sin 150°的值;
(2)若一个三角形的三个内角的比是1∶1∶4,A、B是这个三角形的两个顶点,sin A、cos B是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
第一章 直角三角形的边角关系
2 30°,45°,60°角的三角函数值(一课时)
基础过关
名师点睛
能力提升
以练助学
思维训练
名 师 点 睛
基 础 过 关
C
A
C
90°
解:原式=1-tan 30°+tan 30°=1.
能 力 提 升
B
A
B
1
思 维 训 练
