北师大版九年级下册 2.3 确定二次函数的表达式课件 (共17张PPT)
文档属性
| 名称 | 北师大版九年级下册 2.3 确定二次函数的表达式课件 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:57:47 | ||
图片预览






文档简介
第二章 二次函数
2.3 确定二次函数的表达式(第1课时)
沈旦中学 苏德胜
盛年不重来,一日难再晨。
及时当勉励,岁月不待人。
——送给为中考正努力奔跑的同学们!
1.二次函数表达式的一般形式是什么?
二次函数表达式的顶点式是什么?
y=ax?+bx+c (a,b,c为常数,a ≠0)
y=a(x-h)2+k (a ≠0)
复习引入
1
3 若二次函数y=ax2+bx+c(a不等于0)与x轴两交点为(x1,0)(x2,0),则其函数表达式可以表示成什么形式?(交点式)
y=a(x-x1)(x-x2)
4.我们在用待定系数法确定一次函数y=kx+b(k,b为常数,k≠0 )的关系式时,通常需要几个独立的条件呢?
确定正比例函数y=kx和反比例函数 (k≠0 )关系式时,通常需要几个条件?.
复习引入
1
如果确定二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的关系式时,通常又需要几个条件?
1体会确定二次函数表达式所需的条件。
2会用待定系数法确定二次函数的表达式。
3感受小组合作学习的乐趣,增强团队精神。
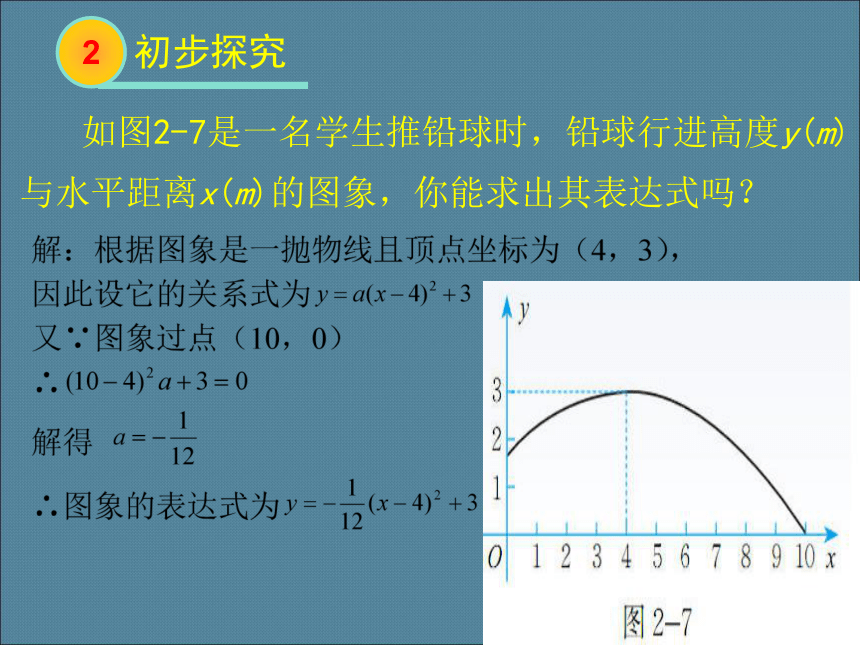
如图2-7是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
初步探究
2
通过前面的探究,你认为确定二次函数的表
达式需要几个条件?小组交流讨论。
确定二次函数的关系式y=ax?+bx+c (a,b,c为常数,a ≠0),通常需要3个条件; 当知道顶点坐标(h,k)和图象上的另一点坐标两个条件时,用顶点式 y=a(x-h)2+k 可以确定二次函数的关系式.
例1 已知二次函数y=ax2+c的图象经过点(2,3)和(-1,-3),求出这个二次函数的表达式.
初步探究
2
解:将点(2,3)和(-1,-3)分别代入二次函数y=ax2+c中,得
3=4a+c,
-3=a+c,
解这个方程组,得
a=2,
c=-5.
∴所求二次函数表达式为:y=2x2-5.
已知二次函数的图象与y轴交点的纵坐标为1, 且经过点(2,5)和(-2,13),求这个二次函数的表达式.{小组讨论}
深入探究
3
在什么情况下,一个二次函数只知道其中两点就可以确定它的表达式?
小结:1.用顶点式y=a(x-h)2+k时,知道顶点(h,k)和图象上的另一点坐标,就可以确定这个二次函数的表达式。
2. 用一般式y=ax?+bx+c确定二次函数时,如果系数a,b,c中有两个是未知的,知道图象上两个点的坐标,也可以确定这个二次函数的关系式.
1.已知二次函数的图象顶点是(-1,1),且经过点(1,-3),求这个二次函数的表达式.
2. 已知二次函数y=x?+bx+c的图象经过点(1,1)与(2,3)两点。求这个二次函数的表达式.
3.已知二次函数图象与x轴交点的横坐标为-2和1,且经过点(0,1),求这个二次函数的表达式.
答案
反馈练习
4
1.通过上述问题的解决,您能体会到求二次函数表达式采用的一般方法是什么?
(待定系数法)
你能否总结出上述解题的一般步骤?
(1)设二次函数的表达式;
(2)根据图象或已知条件列方程(或方程组);
(3)解方程(或方程组),求出待定系数;
(4)答:写出二次函数的表达式.
总结提升
5
用待定系数法确定二次函数关系式的一般步骤和运用的思想方法.
总结提升
5
自我检测
6
1.已知抛物线与x轴交于点M(-1,0)、(2,0),且经过点(1,2),求表达式。
2已知二次函数图像顶点坐标是(2,3),且过点(-1,0)求表达式。
3已知抛物线经过点(-1,-1)(0,-2)(1,1)
(1) 求这个二次函数的解析式。
(2) 指出它的开口方向、对称轴和顶点坐标。
评选出优胜的小组吧!
鲜花和掌声送给你们!
1.02365 =1377.4
0.98365 =0.0006
每天只要努力一点点,坚持一点点,你就会
甩别人很远,你的人生也将大不相同!
2.3 确定二次函数的表达式(第1课时)
沈旦中学 苏德胜
盛年不重来,一日难再晨。
及时当勉励,岁月不待人。
——送给为中考正努力奔跑的同学们!
1.二次函数表达式的一般形式是什么?
二次函数表达式的顶点式是什么?
y=ax?+bx+c (a,b,c为常数,a ≠0)
y=a(x-h)2+k (a ≠0)
复习引入
1
3 若二次函数y=ax2+bx+c(a不等于0)与x轴两交点为(x1,0)(x2,0),则其函数表达式可以表示成什么形式?(交点式)
y=a(x-x1)(x-x2)
4.我们在用待定系数法确定一次函数y=kx+b(k,b为常数,k≠0 )的关系式时,通常需要几个独立的条件呢?
确定正比例函数y=kx和反比例函数 (k≠0 )关系式时,通常需要几个条件?.
复习引入
1
如果确定二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的关系式时,通常又需要几个条件?
1体会确定二次函数表达式所需的条件。
2会用待定系数法确定二次函数的表达式。
3感受小组合作学习的乐趣,增强团队精神。
如图2-7是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
初步探究
2
通过前面的探究,你认为确定二次函数的表
达式需要几个条件?小组交流讨论。
确定二次函数的关系式y=ax?+bx+c (a,b,c为常数,a ≠0),通常需要3个条件; 当知道顶点坐标(h,k)和图象上的另一点坐标两个条件时,用顶点式 y=a(x-h)2+k 可以确定二次函数的关系式.
例1 已知二次函数y=ax2+c的图象经过点(2,3)和(-1,-3),求出这个二次函数的表达式.
初步探究
2
解:将点(2,3)和(-1,-3)分别代入二次函数y=ax2+c中,得
3=4a+c,
-3=a+c,
解这个方程组,得
a=2,
c=-5.
∴所求二次函数表达式为:y=2x2-5.
已知二次函数的图象与y轴交点的纵坐标为1, 且经过点(2,5)和(-2,13),求这个二次函数的表达式.{小组讨论}
深入探究
3
在什么情况下,一个二次函数只知道其中两点就可以确定它的表达式?
小结:1.用顶点式y=a(x-h)2+k时,知道顶点(h,k)和图象上的另一点坐标,就可以确定这个二次函数的表达式。
2. 用一般式y=ax?+bx+c确定二次函数时,如果系数a,b,c中有两个是未知的,知道图象上两个点的坐标,也可以确定这个二次函数的关系式.
1.已知二次函数的图象顶点是(-1,1),且经过点(1,-3),求这个二次函数的表达式.
2. 已知二次函数y=x?+bx+c的图象经过点(1,1)与(2,3)两点。求这个二次函数的表达式.
3.已知二次函数图象与x轴交点的横坐标为-2和1,且经过点(0,1),求这个二次函数的表达式.
答案
反馈练习
4
1.通过上述问题的解决,您能体会到求二次函数表达式采用的一般方法是什么?
(待定系数法)
你能否总结出上述解题的一般步骤?
(1)设二次函数的表达式;
(2)根据图象或已知条件列方程(或方程组);
(3)解方程(或方程组),求出待定系数;
(4)答:写出二次函数的表达式.
总结提升
5
用待定系数法确定二次函数关系式的一般步骤和运用的思想方法.
总结提升
5
自我检测
6
1.已知抛物线与x轴交于点M(-1,0)、(2,0),且经过点(1,2),求表达式。
2已知二次函数图像顶点坐标是(2,3),且过点(-1,0)求表达式。
3已知抛物线经过点(-1,-1)(0,-2)(1,1)
(1) 求这个二次函数的解析式。
(2) 指出它的开口方向、对称轴和顶点坐标。
评选出优胜的小组吧!
鲜花和掌声送给你们!
1.02365 =1377.4
0.98365 =0.0006
每天只要努力一点点,坚持一点点,你就会
甩别人很远,你的人生也将大不相同!
