北师大版九年级下册 1.4 解直角三角形 课件 (共14张PPT)
文档属性
| 名称 | 北师大版九年级下册 1.4 解直角三角形 课件 (共14张PPT) | 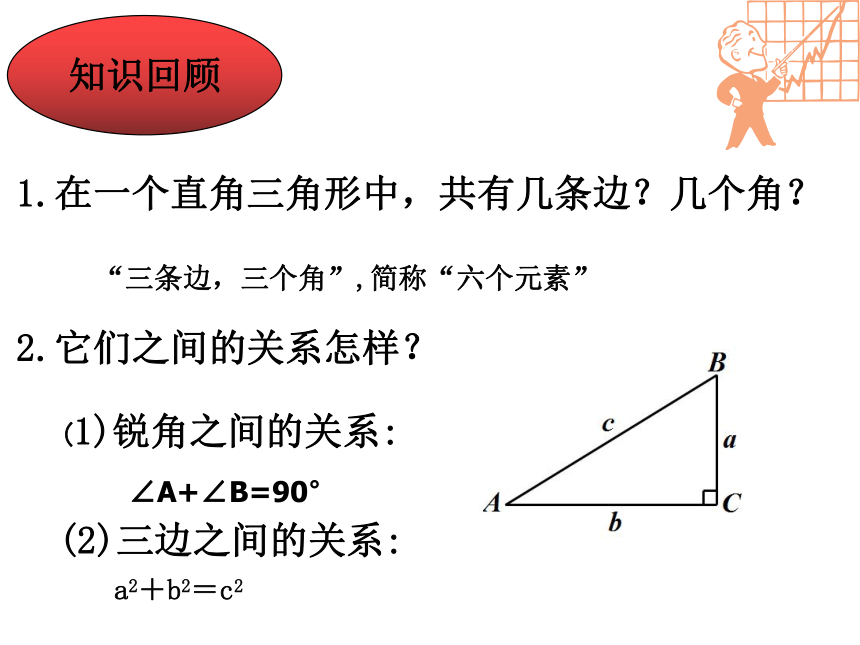 | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:43:18 | ||
图片预览






文档简介
知识回顾
1.在一个直角三角形中,共有几条边?几个角?
2.它们之间的关系怎样?
(1)锐角之间的关系:
(2)三边之间的关系:
“三条边,三个角”,简称“六个元素”
∠A+∠B=90°
a2+b2=c2
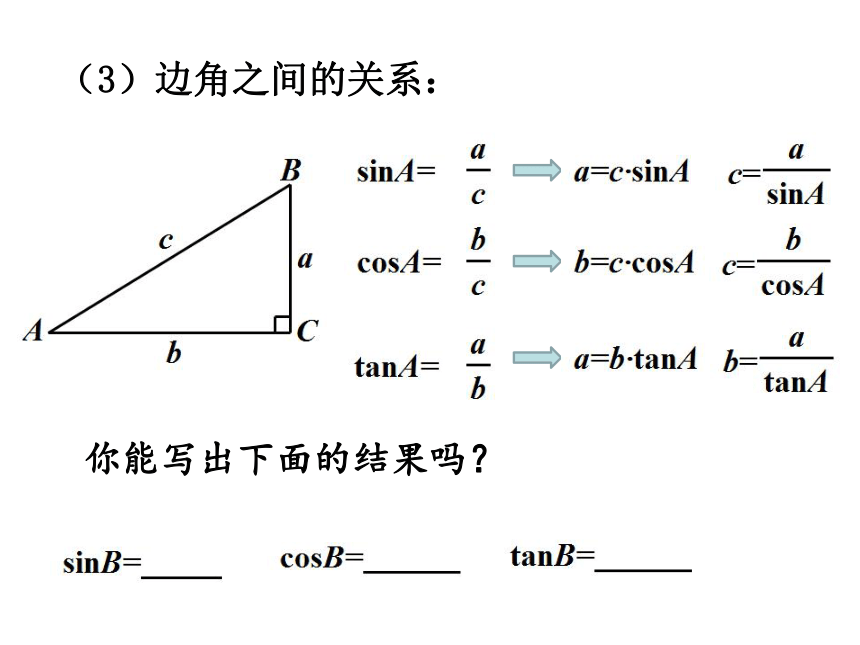
(3)边角之间的关系:
你能写出下面的结果吗?
30°
45°
60°
角α
三角函数
填一填 记一记
点拔:
三关系
解直角三角形
依据
解直角三角形
毕节市赫章县哲庄镇娃多小学 成恒能
议一议(小组合作与探究)
直角三角形中除直角以外还有5个元素,那么
至少知道几个元素,就可以求出其他的元素?
老师:一个元素(边或角)行吗?
学生1:
学生2:
为什么?
老师:猜想:那至少需要几个元素?请看下面这道实际问题。
A
C
B
b
例1 在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,且a = ,b = ,求这个三角形的其他元素。
探究一
a
c
小结
在直角三角形中,已知
两条边(两直角边或者一直角边和斜边)都可以求余下的3个元素。
你发现了什么
解直角三角形定义:
在直角三角形中,由已知元素求所有未知元素的过程。
A
C
B
探究二
小结
例2 在Rt△ABC中,∠C=90°,∠B=25°,b=30,
解这个直角三角形 (精确到0.1,sin25°≈0.4226,cos25°≈0.9063,tan25°≈0.4663)
a
c
b
在直角三角形中,已知一锐角和一边(一锐角和一直角边或者一锐角和斜边)都可以求余下的3个元素。
你发现了什么
想一想
在直角三角形中,如果已知的两个元素是两个锐角,能否求余下的三个元素?为什么?
从探究一、探究二中我们可以发现:
在直角三角形的6个元素中,除直角外,如果知道两个元素,(其中至少有一个是边)就可以求出其余3个元素。
你发现了什么
试问:
在锐角、钝角三角形中告诉两边或者一边一角能否求其他边和角呢?
A
B
C
450
300
2cm
挑战一下
如图,根据图中已知数据,求△ABC其余各边的长,
各角的度数和△ABC的面积.
D
┐
强调:我们本章研究的主角是直角三角形,对于锐角、钝角三角形不能直接运用解直角三角的知识去解答,需作辅助线,使之构成直角三角形再作答。
随堂练习
(P17)
提示:arctan2=63°26?6?,arctan(0.5)=26°33?54?
学习目标
1.掌握解直角三角形的定义
在直角三角形中由已知元素求出所有未知元的过程。
2.探索并归纳由2个元素(至少有一条边)推出其余3个元素的过程。
3.能用解直角三角形的知识来解决简单的计算。
作业:P17-18 1.3(必做) 2.4(选做)
我们的目标达到了吗?
1.在一个直角三角形中,共有几条边?几个角?
2.它们之间的关系怎样?
(1)锐角之间的关系:
(2)三边之间的关系:
“三条边,三个角”,简称“六个元素”
∠A+∠B=90°
a2+b2=c2
(3)边角之间的关系:
你能写出下面的结果吗?
30°
45°
60°
角α
三角函数
填一填 记一记
点拔:
三关系
解直角三角形
依据
解直角三角形
毕节市赫章县哲庄镇娃多小学 成恒能
议一议(小组合作与探究)
直角三角形中除直角以外还有5个元素,那么
至少知道几个元素,就可以求出其他的元素?
老师:一个元素(边或角)行吗?
学生1:
学生2:
为什么?
老师:猜想:那至少需要几个元素?请看下面这道实际问题。
A
C
B
b
例1 在 Rt△ABC 中,∠C 为直角,∠A,∠B,∠C 所对的边分别为 a,b,c,且a = ,b = ,求这个三角形的其他元素。
探究一
a
c
小结
在直角三角形中,已知
两条边(两直角边或者一直角边和斜边)都可以求余下的3个元素。
你发现了什么
解直角三角形定义:
在直角三角形中,由已知元素求所有未知元素的过程。
A
C
B
探究二
小结
例2 在Rt△ABC中,∠C=90°,∠B=25°,b=30,
解这个直角三角形 (精确到0.1,sin25°≈0.4226,cos25°≈0.9063,tan25°≈0.4663)
a
c
b
在直角三角形中,已知一锐角和一边(一锐角和一直角边或者一锐角和斜边)都可以求余下的3个元素。
你发现了什么
想一想
在直角三角形中,如果已知的两个元素是两个锐角,能否求余下的三个元素?为什么?
从探究一、探究二中我们可以发现:
在直角三角形的6个元素中,除直角外,如果知道两个元素,(其中至少有一个是边)就可以求出其余3个元素。
你发现了什么
试问:
在锐角、钝角三角形中告诉两边或者一边一角能否求其他边和角呢?
A
B
C
450
300
2cm
挑战一下
如图,根据图中已知数据,求△ABC其余各边的长,
各角的度数和△ABC的面积.
D
┐
强调:我们本章研究的主角是直角三角形,对于锐角、钝角三角形不能直接运用解直角三角的知识去解答,需作辅助线,使之构成直角三角形再作答。
随堂练习
(P17)
提示:arctan2=63°26?6?,arctan(0.5)=26°33?54?
学习目标
1.掌握解直角三角形的定义
在直角三角形中由已知元素求出所有未知元的过程。
2.探索并归纳由2个元素(至少有一条边)推出其余3个元素的过程。
3.能用解直角三角形的知识来解决简单的计算。
作业:P17-18 1.3(必做) 2.4(选做)
我们的目标达到了吗?
