北师大版九年级下册1.1《正弦与余弦》课件 (共22张PPT)
文档属性
| 名称 | 北师大版九年级下册1.1《正弦与余弦》课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:38:09 | ||
图片预览




文档简介
锐角三角函数
§1.1
九年级下册 第一章直角三角形的边角关系
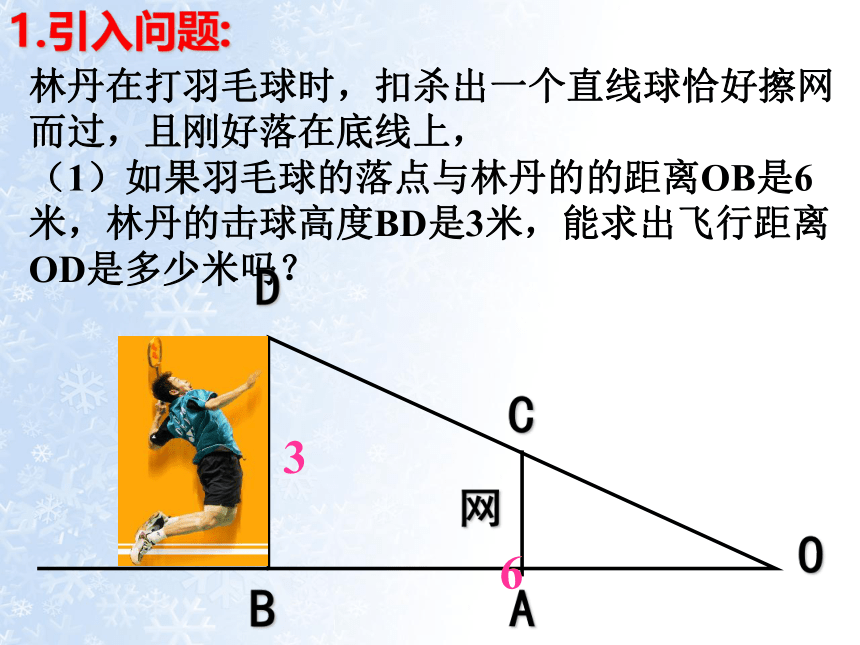
林丹在打羽毛球时,扣杀出一个直线球恰好擦网而过,且刚好落在底线上,
(1)如果羽毛球的落点与林丹的的距离OB是6米,林丹的击球高度BD是3米,能求出飞行距离OD是多少米吗?
1.引入问题:
O
A
C
B
D
网
3
6
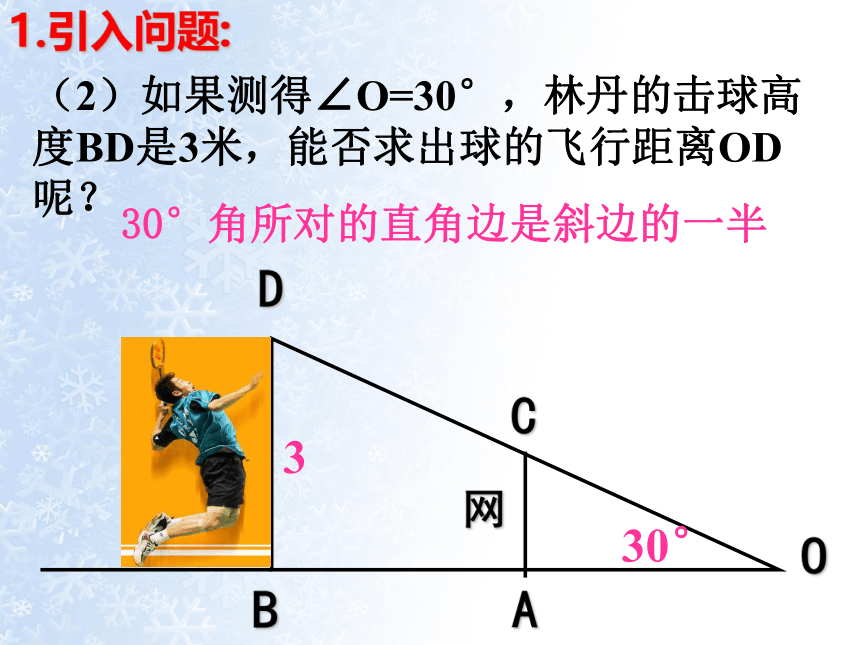
(2)如果测得∠O=30°,林丹的击球高度BD是3米,能否求出球的飞行距离OD呢?
O
A
C
B
D
网
1.引入问题:
30°角所对的直角边是斜边的一半
30°
3
2.探究问题:
(1)在Rt△ABC中,∠C=90°, ∠A=30°,则
30°
6
A
B
C
∠A的对边
斜边
=
n
结论:直角三角形中,30°角的对边与斜边的比值是定值
2.探究问题:
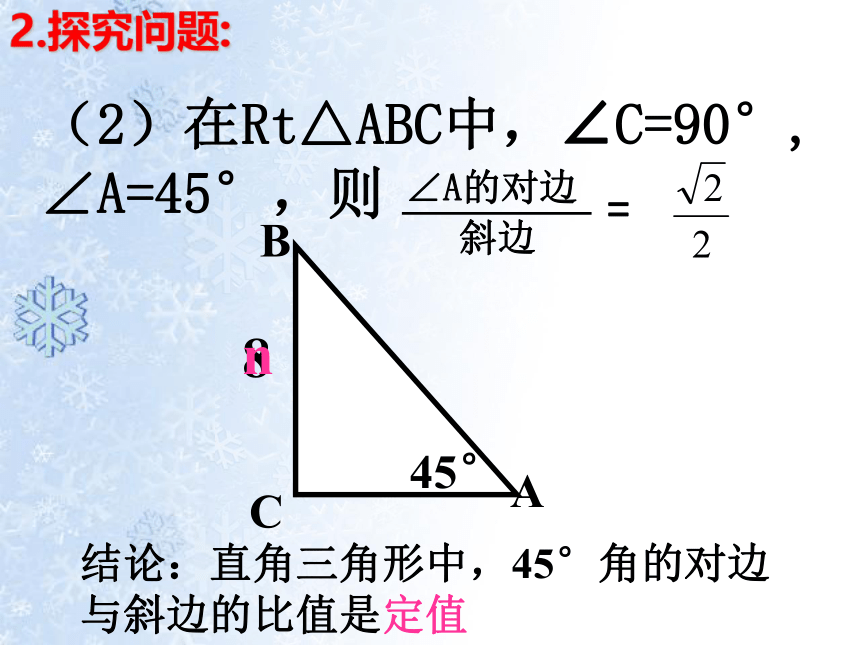
(2)在Rt△ABC中,∠C=90°, ∠A=45°,则
∠A的对边
斜边
=
45°
8
A
B
C
n
结论:直角三角形中,45°角的对边与斜边的比值是定值
2.探究问题:
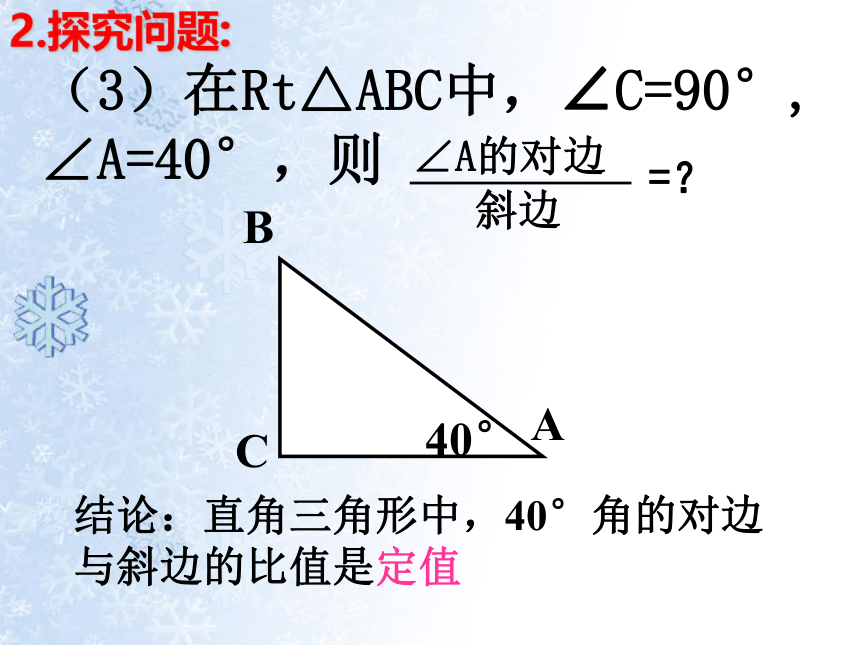
(3)在Rt△ABC中,∠C=90°, ∠A=40°,则
B
∠A的对边
斜边
=?
40°
A
C
结论:直角三角形中,40°角的对边与斜边的比值是定值
在Rt△ABC中, ∠ C=90°,∠A的值确定后,∠A的对边与斜边的比值是一个定值吗?
规律一:
当∠A的大小相等时,比值也相等
规律二:
当∠A的大小变化时,比值也变化
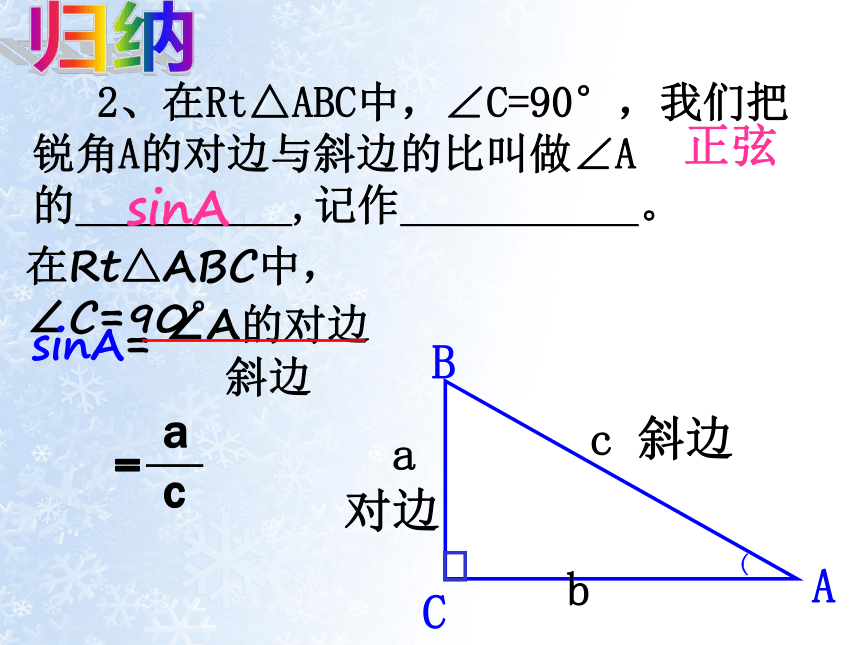
2、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的 ,记作 。
在Rt△ABC中,∠C=90°
∠A的对边
sinA=
斜边
a
c
=
sinA
A
B
C
c 斜边
b
a
对边
正弦
(
1、填空:
(1)已知Rt△ABC中,∠C=90°,若AB=10,BC=6,
则sinA= ;sinB= ;
A
10m
6m
B
C
1、填空:
(2)如图:P是∠α?的边OA上一点,且P点的坐标为(3,4),
则sinα=_______.
α
例题
如图,在Rt △ABC中,∠C=90°,
AB=13,BC=5
求sinA和sinB的值.
解:在Rt △ABC中,
B
A
C
5
13
练一练
A
B
C
3
4
2、在Rt△ABC中, ∠C=90°,
求sinA和sinB的值。
3、填空已知:如图,在△ABC中,∠C=90°,sinA= ,
(1)BC=2,则AB= ;
(2) BC=4,则AB= .
3
6
变式,已知:如图,在△ABC中,
∠C=90°,sinA=
则sinB=
看谁快
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
练一练
4.如图
A
C
B
3
7
300
则 sinA=______ .
1
2
5.△ABC中,AB=8,BC=6,△ABC的面积是12,求sinB的值.
A
B
C
【变一变】
已知△ABC中,
AB=8,BC=6,sinA =
试求△ABC的面积.
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。
6、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?
想一想
若AC=5,CD=3,求sinB的值.
┌
A
C
B
D
解: ∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中,AD=
sin ∠ACD=
∴sinB=
=4
小结 拓展
锐角三角函数:正弦
A
B
C
∠A的对边
┌
斜边
斜边
∠A的对边
sinA=
7、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。
8.已知在RT△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.
A
B
C
D
E
§1.1
九年级下册 第一章直角三角形的边角关系
林丹在打羽毛球时,扣杀出一个直线球恰好擦网而过,且刚好落在底线上,
(1)如果羽毛球的落点与林丹的的距离OB是6米,林丹的击球高度BD是3米,能求出飞行距离OD是多少米吗?
1.引入问题:
O
A
C
B
D
网
3
6
(2)如果测得∠O=30°,林丹的击球高度BD是3米,能否求出球的飞行距离OD呢?
O
A
C
B
D
网
1.引入问题:
30°角所对的直角边是斜边的一半
30°
3
2.探究问题:
(1)在Rt△ABC中,∠C=90°, ∠A=30°,则
30°
6
A
B
C
∠A的对边
斜边
=
n
结论:直角三角形中,30°角的对边与斜边的比值是定值
2.探究问题:
(2)在Rt△ABC中,∠C=90°, ∠A=45°,则
∠A的对边
斜边
=
45°
8
A
B
C
n
结论:直角三角形中,45°角的对边与斜边的比值是定值
2.探究问题:
(3)在Rt△ABC中,∠C=90°, ∠A=40°,则
B
∠A的对边
斜边
=?
40°
A
C
结论:直角三角形中,40°角的对边与斜边的比值是定值
在Rt△ABC中, ∠ C=90°,∠A的值确定后,∠A的对边与斜边的比值是一个定值吗?
规律一:
当∠A的大小相等时,比值也相等
规律二:
当∠A的大小变化时,比值也变化
2、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的 ,记作 。
在Rt△ABC中,∠C=90°
∠A的对边
sinA=
斜边
a
c
=
sinA
A
B
C
c 斜边
b
a
对边
正弦
(
1、填空:
(1)已知Rt△ABC中,∠C=90°,若AB=10,BC=6,
则sinA= ;sinB= ;
A
10m
6m
B
C
1、填空:
(2)如图:P是∠α?的边OA上一点,且P点的坐标为(3,4),
则sinα=_______.
α
例题
如图,在Rt △ABC中,∠C=90°,
AB=13,BC=5
求sinA和sinB的值.
解:在Rt △ABC中,
B
A
C
5
13
练一练
A
B
C
3
4
2、在Rt△ABC中, ∠C=90°,
求sinA和sinB的值。
3、填空已知:如图,在△ABC中,∠C=90°,sinA= ,
(1)BC=2,则AB= ;
(2) BC=4,则AB= .
3
6
变式,已知:如图,在△ABC中,
∠C=90°,sinA=
则sinB=
看谁快
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
练一练
4.如图
A
C
B
3
7
300
则 sinA=______ .
1
2
5.△ABC中,AB=8,BC=6,△ABC的面积是12,求sinB的值.
A
B
C
【变一变】
已知△ABC中,
AB=8,BC=6,sinA =
试求△ABC的面积.
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。
6、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?
想一想
若AC=5,CD=3,求sinB的值.
┌
A
C
B
D
解: ∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中,AD=
sin ∠ACD=
∴sinB=
=4
小结 拓展
锐角三角函数:正弦
A
B
C
∠A的对边
┌
斜边
斜边
∠A的对边
sinA=
7、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。
8.已知在RT△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.
A
B
C
D
E
