北师大版九年级下册数学 1.4 解直角三角形 (14张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 1.4 解直角三角形 (14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 500.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:50:49 | ||
图片预览





文档简介
第一章 直角三角形的边角关系
1.4 解直角三角形
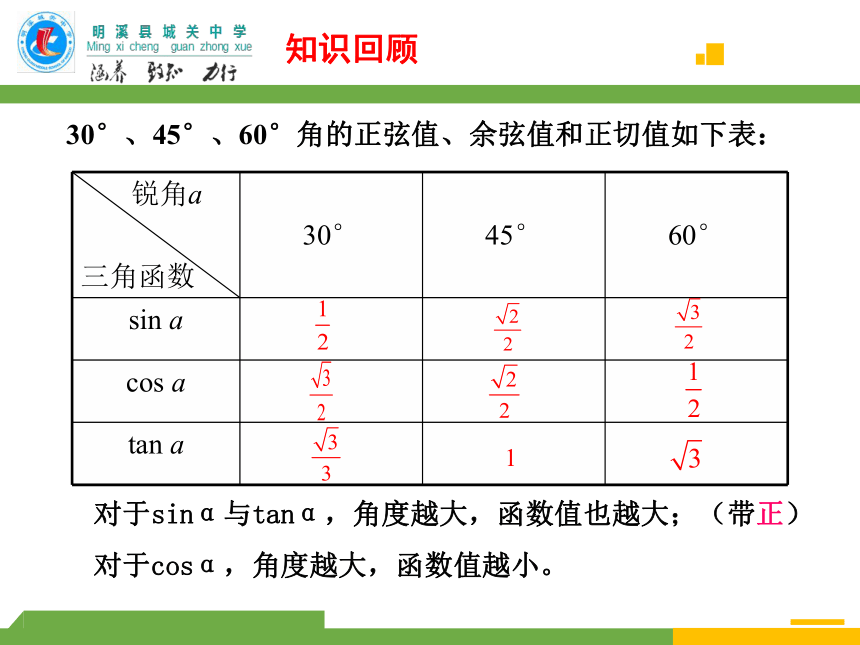
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
知识回顾
(1)在直角三角形中,除直角外共有几个元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
A
B
C
c
b
a
情境引入
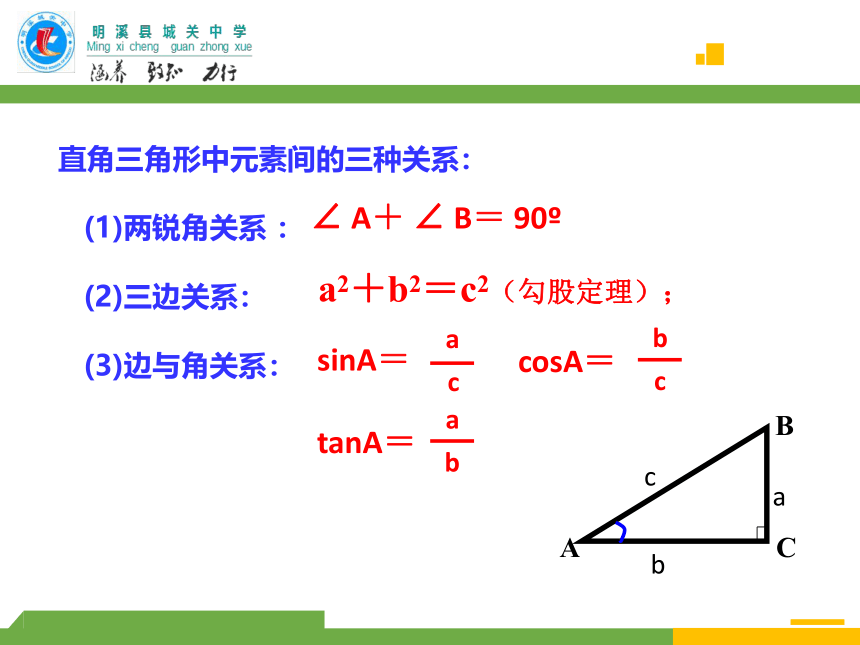
直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
A
B
C
c
b
a
a2+b2=c2(勾股定理);
a
c
∠ A+ ∠ B= 90?
sinA=
b
c
cosA=
tanA=
a
b
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
自主预习
定义:
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.
新知探究
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程.
解直角三角形
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
问题:1、解直角三角形需要什么条件?
议一议
2、解直角三角形的条件可分为哪几类?
探究一、已知两条边解直角三角形:
例1 在RT△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=√15,b=5,求这个三角形的其他元素。
由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形。
探究二、
已知一条边和一个锐角 (两个已知元素中至少有一条边)解直角三角形:
例2 在RT△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°求这个三角形的其他元素(边长精确到1)。
1.在△ABC中,∠C=90°,解这个直角三角形.
(1)∠A=60°,斜边上的高CD = ;
(2)∠A=60°,a+b=3+ .
解:(1)∠B = 90°-∠A = 30°
AC=
60°
A
B
C
D
┓
┓
随堂练习
2.在Rt△ABC中∠C=90°,AD=2AC=2BD,且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
CE=5
2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)
1、解直角三角形除直角外,至少要知道两个元素
(这两个元素中至少有一条边)
小结
1.4 解直角三角形
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小。
知识回顾
(1)在直角三角形中,除直角外共有几个元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
A
B
C
c
b
a
情境引入
直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
A
B
C
c
b
a
a2+b2=c2(勾股定理);
a
c
∠ A+ ∠ B= 90?
sinA=
b
c
cosA=
tanA=
a
b
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
自主预习
定义:
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.
新知探究
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程.
解直角三角形
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
问题:1、解直角三角形需要什么条件?
议一议
2、解直角三角形的条件可分为哪几类?
探究一、已知两条边解直角三角形:
例1 在RT△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=√15,b=5,求这个三角形的其他元素。
由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形。
探究二、
已知一条边和一个锐角 (两个已知元素中至少有一条边)解直角三角形:
例2 在RT△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°求这个三角形的其他元素(边长精确到1)。
1.在△ABC中,∠C=90°,解这个直角三角形.
(1)∠A=60°,斜边上的高CD = ;
(2)∠A=60°,a+b=3+ .
解:(1)∠B = 90°-∠A = 30°
AC=
60°
A
B
C
D
┓
┓
随堂练习
2.在Rt△ABC中∠C=90°,AD=2AC=2BD,且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
CE=5
2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)
1、解直角三角形除直角外,至少要知道两个元素
(这两个元素中至少有一条边)
小结
