北师大版九年级下册数学2.4 二次函数在销售方面的应用 (共21张PPT)
文档属性
| 名称 | 北师大版九年级下册数学2.4 二次函数在销售方面的应用 (共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 18:45:55 | ||
图片预览





文档简介
1、复习二次函数y=ax2+bx+c(a≠0)的相关性质:
试一试:
顶点坐标
对称轴
最值
增减性
开口方向
y
x
o
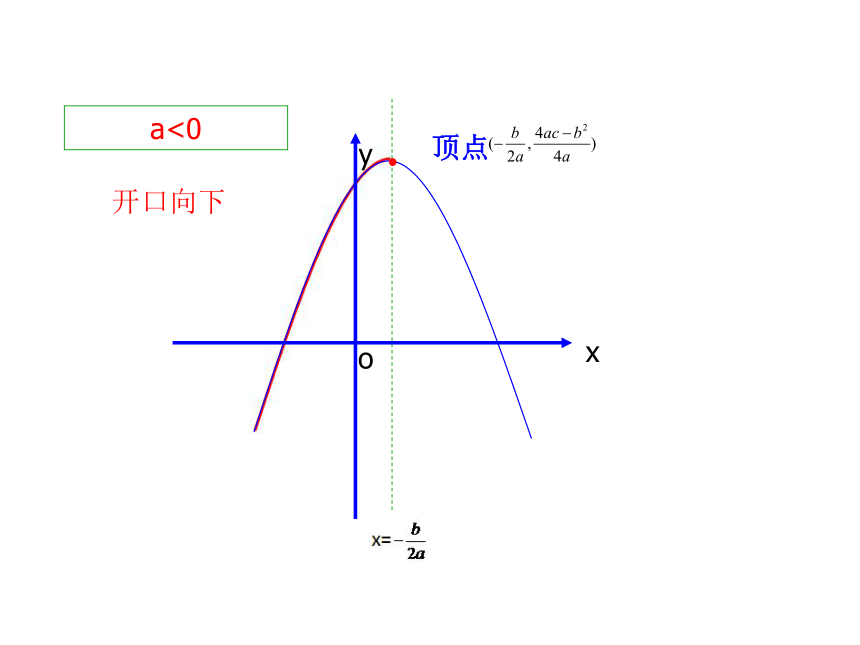
顶点
a<0
开口向下
y
x
o
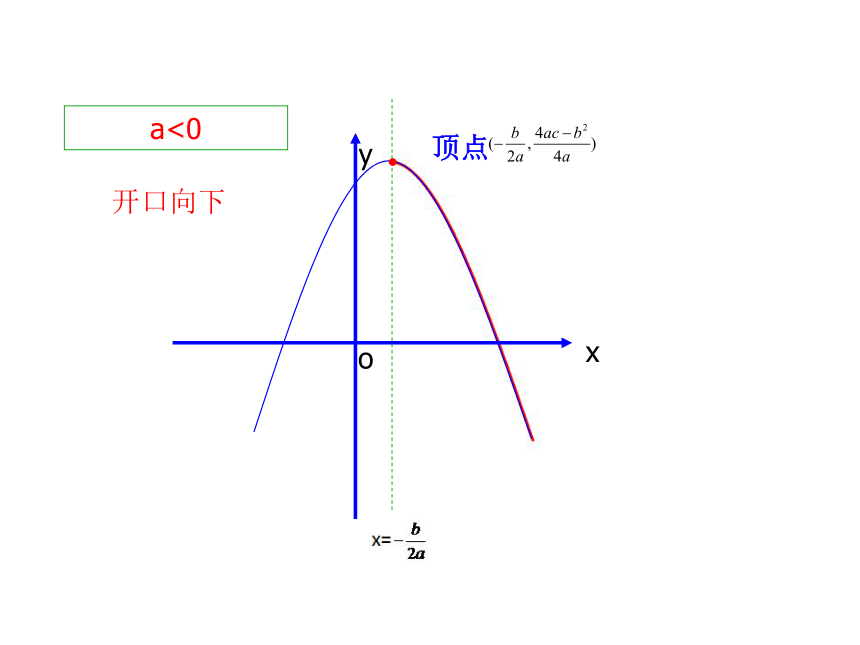
顶点
a<0
开口向下
y
x
o
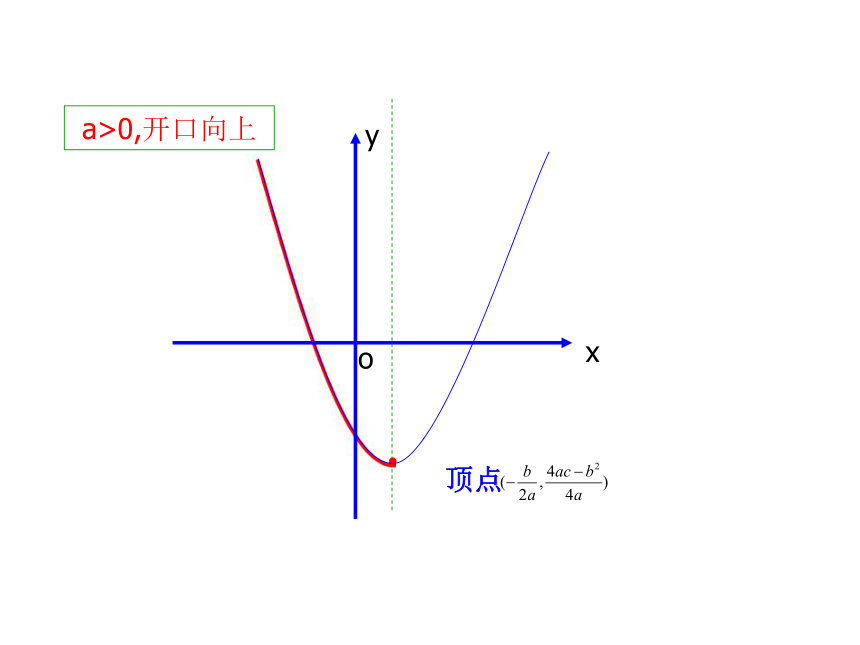
顶点
a>0,开口向上
y
x
o
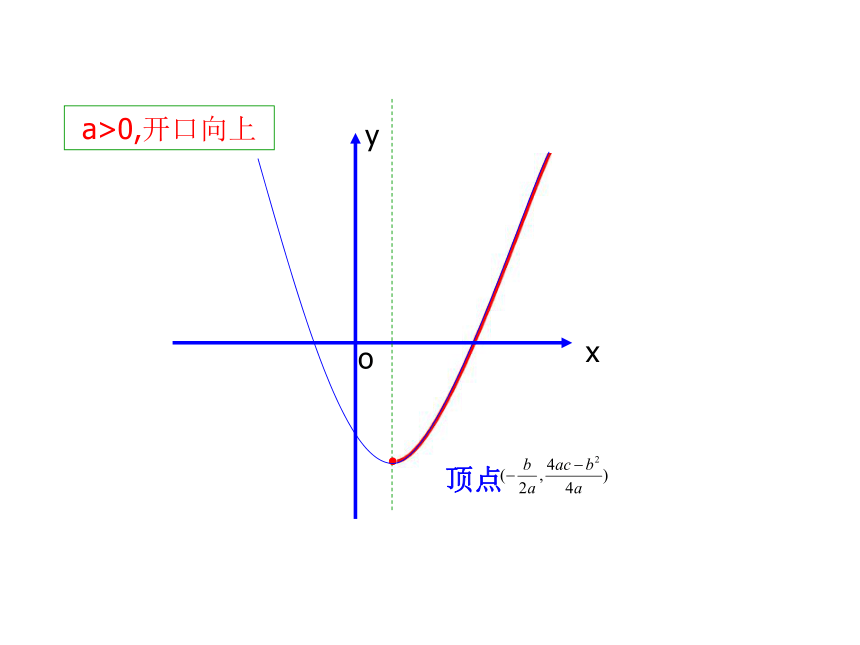
顶点
a>0,开口向上
试一试:
2.复习这节课所要用的其他相关知识:
利润=售价-进价,
总利润=每件利润×销售 量
求出下列函数的最值
y=-10x2+100x+6000
例1、我校教学楼后有一块空地,学校准备靠墙修建一个矩形花圃(墙长50米),郭大爷买回了总长为40米的栅栏准备将花圃围住(如图所示),问应如何围,才能使花圃的面积最大?
想一想:若每件涨价x元则此商品
(1)每件利润为?????????????元。
(2)每星期销售量可以表示为?????????????;
(3)所获利润可以表示为???????????;
例2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映,如果调整价格,每涨价1元,每星期少卖10件,每降价1元。每星期多卖18件,已知商品的进价为每件40元,如何定价才能获得最大利润?
讨论涨价与降价都有可能获得最大利润吗?
讨论:1、涨价情况下最大利润是多少?
解:设每星期所获利润为w元,则
w=( )( )
w=(60-40+x )(300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250
∵a=-10<0 ∴抛物线开口向下
∴x=5时 w有最大值是6250
答:在涨价情况下,涨价5元,定价65元时,每星期所获利润最大,最大利润是6250元。
想一想:若每件售价x元则此商品
(1)每件利润为?????????????元。
(2)每星期销售量可以表示为?????????????;
(3)所获利润可以表示为???????????;
试一试:
温馨提示:同桌交流,互相帮助!
2、在降价情况下,最大利润又是多少?
我们用类似的方法进行分析:
=-18(x-2)2+6050
∵a=-18<0 ∴抛物线开口向下
∴x=2时 w有最大值是6050
答:降价情况下,降价2元,定价58元时,利润最大,最大利润是6050元
设每件降价x元,所获利润为w元,则有
w=(60-40-x )(300+18x)
如果设售价为 x元呢?
例3:某商场试销一种成本 为每件60元的服装,规定试销期间单价不低于成本单价,且获利不得高于45%,经试销发现,
销售量y(件)与销售单价x(元)符合如下表的一次函数关系:
(1)求销售量y与销售单价x之间的函数关系式,并写出自变量x的取值范围;
(2)若该商场获得利润为w元,试写出利润w与销售单价x之
间的函数关系式,并求出销售单价定为多少元时,商场可获得
最大利润,最大利润是多少元?
x
…
60
65
70
75
80
…
y
…
60
55
50
45
40
…
例4:
1、某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件。如何提高售价,才能在半个月内获得最大利润?
解:设销售单价为x元,销售利润为w元,则
1.某商家以每件50元的价钱购进一批新型产品,如果按每件60元出售,那么每周可销售500件。根据试销规律,这种产品的销售单价每提高1元,其销售量每周相应减少10件,但每件产品的销售单价不低于60元,且不能高于85元。设每周的销售量为y(件),这种产品的销售单价为x(元),解答下列问题:
请直接写出?y与x的函数关系式;
商家要想每周获得8000元的销售利润,销售单价应定为多少元?
销售单价为多少元时,每周获得的销售利润最大?最大利润是多少元?
2.某果园有100棵橙子树,平均每棵树结600个橙子。现准备多种一些橙子树以提高果园产品量,但是如果多种树,那么树之间的距离和每棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子, 问增种多少棵橙子时,产量最大?最大产量是多少?
试一试:
顶点坐标
对称轴
最值
增减性
开口方向
y
x
o
顶点
a<0
开口向下
y
x
o
顶点
a<0
开口向下
y
x
o
顶点
a>0,开口向上
y
x
o
顶点
a>0,开口向上
试一试:
2.复习这节课所要用的其他相关知识:
利润=售价-进价,
总利润=每件利润×销售 量
求出下列函数的最值
y=-10x2+100x+6000
例1、我校教学楼后有一块空地,学校准备靠墙修建一个矩形花圃(墙长50米),郭大爷买回了总长为40米的栅栏准备将花圃围住(如图所示),问应如何围,才能使花圃的面积最大?
想一想:若每件涨价x元则此商品
(1)每件利润为?????????????元。
(2)每星期销售量可以表示为?????????????;
(3)所获利润可以表示为???????????;
例2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映,如果调整价格,每涨价1元,每星期少卖10件,每降价1元。每星期多卖18件,已知商品的进价为每件40元,如何定价才能获得最大利润?
讨论涨价与降价都有可能获得最大利润吗?
讨论:1、涨价情况下最大利润是多少?
解:设每星期所获利润为w元,则
w=( )( )
w=(60-40+x )(300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250
∵a=-10<0 ∴抛物线开口向下
∴x=5时 w有最大值是6250
答:在涨价情况下,涨价5元,定价65元时,每星期所获利润最大,最大利润是6250元。
想一想:若每件售价x元则此商品
(1)每件利润为?????????????元。
(2)每星期销售量可以表示为?????????????;
(3)所获利润可以表示为???????????;
试一试:
温馨提示:同桌交流,互相帮助!
2、在降价情况下,最大利润又是多少?
我们用类似的方法进行分析:
=-18(x-2)2+6050
∵a=-18<0 ∴抛物线开口向下
∴x=2时 w有最大值是6050
答:降价情况下,降价2元,定价58元时,利润最大,最大利润是6050元
设每件降价x元,所获利润为w元,则有
w=(60-40-x )(300+18x)
如果设售价为 x元呢?
例3:某商场试销一种成本 为每件60元的服装,规定试销期间单价不低于成本单价,且获利不得高于45%,经试销发现,
销售量y(件)与销售单价x(元)符合如下表的一次函数关系:
(1)求销售量y与销售单价x之间的函数关系式,并写出自变量x的取值范围;
(2)若该商场获得利润为w元,试写出利润w与销售单价x之
间的函数关系式,并求出销售单价定为多少元时,商场可获得
最大利润,最大利润是多少元?
x
…
60
65
70
75
80
…
y
…
60
55
50
45
40
…
例4:
1、某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件。如何提高售价,才能在半个月内获得最大利润?
解:设销售单价为x元,销售利润为w元,则
1.某商家以每件50元的价钱购进一批新型产品,如果按每件60元出售,那么每周可销售500件。根据试销规律,这种产品的销售单价每提高1元,其销售量每周相应减少10件,但每件产品的销售单价不低于60元,且不能高于85元。设每周的销售量为y(件),这种产品的销售单价为x(元),解答下列问题:
请直接写出?y与x的函数关系式;
商家要想每周获得8000元的销售利润,销售单价应定为多少元?
销售单价为多少元时,每周获得的销售利润最大?最大利润是多少元?
2.某果园有100棵橙子树,平均每棵树结600个橙子。现准备多种一些橙子树以提高果园产品量,但是如果多种树,那么树之间的距离和每棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子, 问增种多少棵橙子时,产量最大?最大产量是多少?
