北师大版九年级下数学1.5解直角三角形的应用3-坡度课件(共16张PPT)
文档属性
| 名称 | 北师大版九年级下数学1.5解直角三角形的应用3-坡度课件(共16张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览




文档简介
初 中 数 学 九 年 级 下册
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF
≈4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
一个公共房屋门前的台阶共高出地面1.2米.台阶被拆除后,换成供轮椅行走的斜坡.根据这个城市的规定,轮椅行走斜坡的倾斜角不得超过30°.从斜坡的起点至楼门的最短的水平距离该是多少?(精确到0.1米)
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
——坡度、坡角
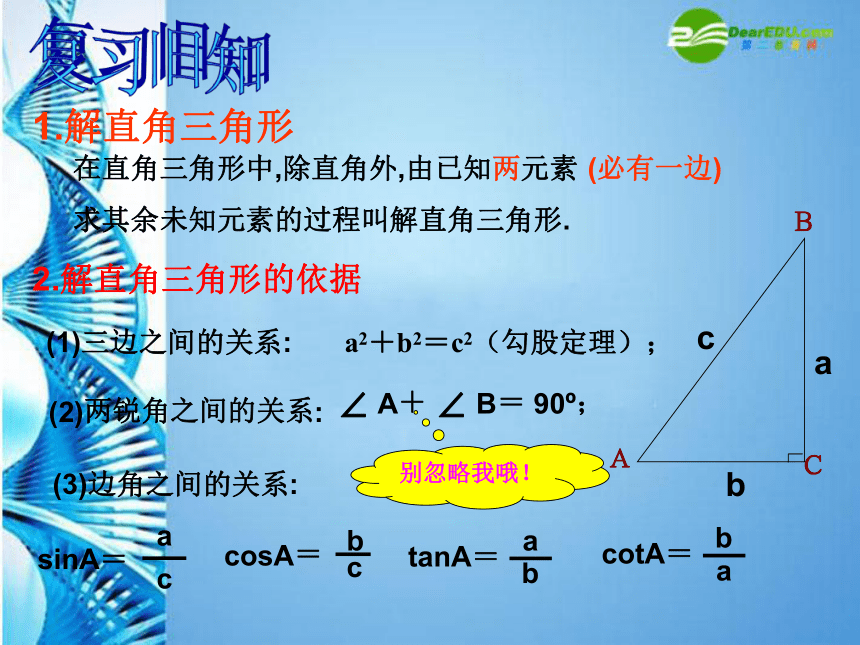
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
cotA=
b
a
A
C
B
a
b
c
别忽略我哦!
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的 ,斜坡CD的 ,
则斜坡CD的 ,
坝底宽AD和斜坡AB
的长应设计为多少?
坡度i=1∶3
坡度i=1∶2.5
坡面角α
A
D
B
C
i=1:2.5
23
6
α
l
h
i= h : l
1、坡角
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即 i=——
h
l
3、坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
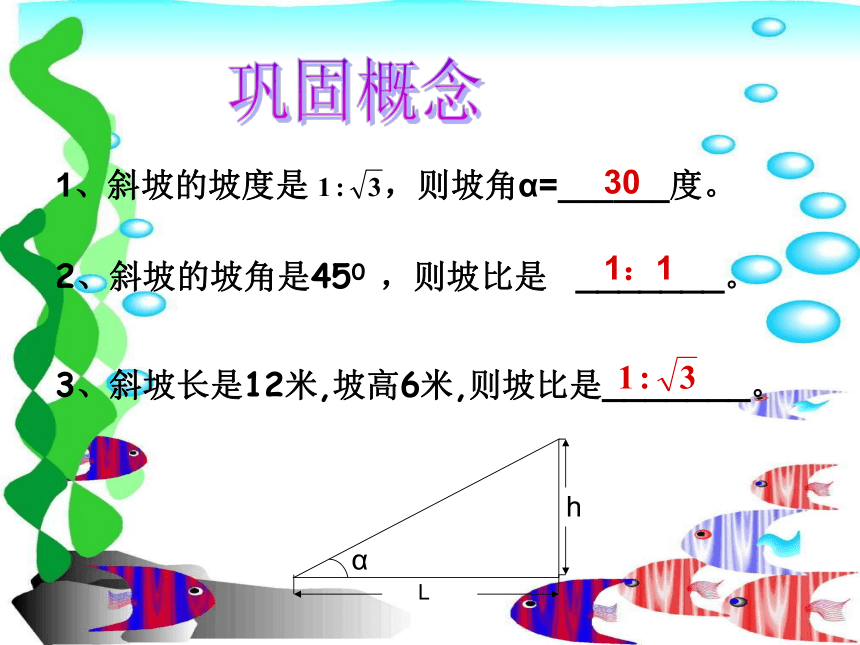
1、斜坡的坡度是 ,则坡角α=______度。
2、斜坡的坡角是450 ,则坡比是 _______。
3、斜坡长是12米,坡高6米,则坡比是_______。
α
L
h
30
1:1
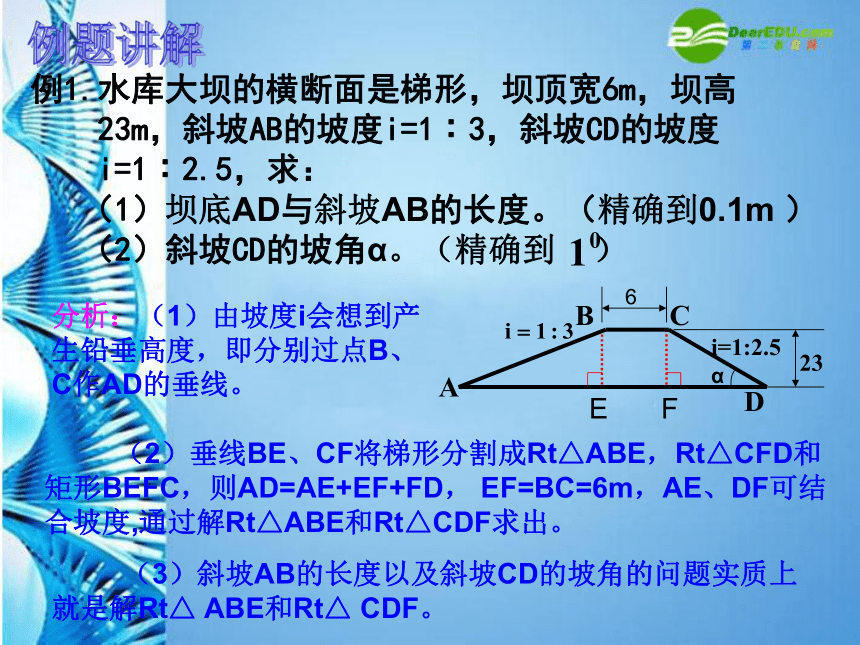
例1.水库大坝的横断面是梯形,坝顶宽6m,坝高
23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度
i=1∶2.5,求:
(1)坝底AD与斜坡AB的长度。(精确到0.1m )
(2)斜坡CD的坡角α。(精确到 )
E
F
A
D
B
C
i=1:2.5
23
6
α
分析:(1)由坡度i会想到产生铅垂高度,即分别过点B、C作AD的垂线。
(2)垂线BE、CF将梯形分割成Rt△ABE,Rt△CFD和矩形BEFC,则AD=AE+EF+FD, EF=BC=6m,AE、DF可结合坡度,通过解Rt△ABE和Rt△CDF求出。
(3)斜坡AB的长度以及斜坡CD的坡角的问题实质上就是解Rt△ ABE和Rt△ CDF。
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,
垂足分别为点E、 F,由题意可知
在Rt△ABE中
BE=CF=23m EF=BC=6m
在Rt△DCF中,同理可得
=69+6+57.5
=132.5m
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度i=tanα=1:2.5=0.4
由计算器可算得
E
F
A
D
B
C
i=1:2.5
23
6
α
答:坝底宽AD为132.5米,斜坡AB
的长约为72.7米.斜坡CD的坡角α约
为22°。
一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽.(精确到0.1米 ) ?
45°
30°
4米
12米
A
B
C
E
F
D
45°
30°
4米
12米
A
B
C
E
F
D
1.2
1.2
30°
A
B
C
为了增加抗洪能力,现将横断面如图所示的大坝加高,加高部分的横断面为梯形DCGH,GH∥CD,点G、H分别在AD、BC的延长线上,当新大坝坝顶宽为4.8米时,大坝加高了几米?
B
A
C
D
i1=1:1.2
i2=1:0.8
G
H
6米
E
F
M
N
思考:如图是某公路路基的设计简图,等腰梯形ABCD表示它的横断面,原计划设计的坡角为A=22°37′,坡长AD=6. 5米,现考虑到在短期内车流量会增加,需增加路面宽度,故改变设计方案,将图中1,2两部分分别补到3,4的位置,使横断面EFGH为等腰梯形,重新设计后路基的坡角为32°,全部工程的用土量不变,问:路面宽将增加多少?
(选用数据:sin22°37′≈ ,cos22°37′ ≈ ,
tan 22°37′ ≈ ,
tan 32° ≈ )
A
E
C
D
B
F
G
H
1
2
3
4
M
N
本节课你有什么收获?
收获经验
2、解直角三角形的问题往往与其他知识联系,因此,我们要善于要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
1、学以致用
我们学习数学的目的就是解决实际生活中存在的数学问题,因此,在解题时首先要读懂题意,把实际问题转化为数学问题。
对于生活中存在的解直角三角形的问题,关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线)。
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF
≈4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
一个公共房屋门前的台阶共高出地面1.2米.台阶被拆除后,换成供轮椅行走的斜坡.根据这个城市的规定,轮椅行走斜坡的倾斜角不得超过30°.从斜坡的起点至楼门的最短的水平距离该是多少?(精确到0.1米)
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
——坡度、坡角
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
cotA=
b
a
A
C
B
a
b
c
别忽略我哦!
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的 ,斜坡CD的 ,
则斜坡CD的 ,
坝底宽AD和斜坡AB
的长应设计为多少?
坡度i=1∶3
坡度i=1∶2.5
坡面角α
A
D
B
C
i=1:2.5
23
6
α
l
h
i= h : l
1、坡角
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即 i=——
h
l
3、坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
1、斜坡的坡度是 ,则坡角α=______度。
2、斜坡的坡角是450 ,则坡比是 _______。
3、斜坡长是12米,坡高6米,则坡比是_______。
α
L
h
30
1:1
例1.水库大坝的横断面是梯形,坝顶宽6m,坝高
23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度
i=1∶2.5,求:
(1)坝底AD与斜坡AB的长度。(精确到0.1m )
(2)斜坡CD的坡角α。(精确到 )
E
F
A
D
B
C
i=1:2.5
23
6
α
分析:(1)由坡度i会想到产生铅垂高度,即分别过点B、C作AD的垂线。
(2)垂线BE、CF将梯形分割成Rt△ABE,Rt△CFD和矩形BEFC,则AD=AE+EF+FD, EF=BC=6m,AE、DF可结合坡度,通过解Rt△ABE和Rt△CDF求出。
(3)斜坡AB的长度以及斜坡CD的坡角的问题实质上就是解Rt△ ABE和Rt△ CDF。
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,
垂足分别为点E、 F,由题意可知
在Rt△ABE中
BE=CF=23m EF=BC=6m
在Rt△DCF中,同理可得
=69+6+57.5
=132.5m
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度i=tanα=1:2.5=0.4
由计算器可算得
E
F
A
D
B
C
i=1:2.5
23
6
α
答:坝底宽AD为132.5米,斜坡AB
的长约为72.7米.斜坡CD的坡角α约
为22°。
一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽.(精确到0.1米 ) ?
45°
30°
4米
12米
A
B
C
E
F
D
45°
30°
4米
12米
A
B
C
E
F
D
1.2
1.2
30°
A
B
C
为了增加抗洪能力,现将横断面如图所示的大坝加高,加高部分的横断面为梯形DCGH,GH∥CD,点G、H分别在AD、BC的延长线上,当新大坝坝顶宽为4.8米时,大坝加高了几米?
B
A
C
D
i1=1:1.2
i2=1:0.8
G
H
6米
E
F
M
N
思考:如图是某公路路基的设计简图,等腰梯形ABCD表示它的横断面,原计划设计的坡角为A=22°37′,坡长AD=6. 5米,现考虑到在短期内车流量会增加,需增加路面宽度,故改变设计方案,将图中1,2两部分分别补到3,4的位置,使横断面EFGH为等腰梯形,重新设计后路基的坡角为32°,全部工程的用土量不变,问:路面宽将增加多少?
(选用数据:sin22°37′≈ ,cos22°37′ ≈ ,
tan 22°37′ ≈ ,
tan 32° ≈ )
A
E
C
D
B
F
G
H
1
2
3
4
M
N
本节课你有什么收获?
收获经验
2、解直角三角形的问题往往与其他知识联系,因此,我们要善于要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
1、学以致用
我们学习数学的目的就是解决实际生活中存在的数学问题,因此,在解题时首先要读懂题意,把实际问题转化为数学问题。
对于生活中存在的解直角三角形的问题,关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线)。
