北师大版七年级数学上册第4章第5节多边形和圆的初步认识课件(21张PPT)
文档属性
| 名称 | 北师大版七年级数学上册第4章第5节多边形和圆的初步认识课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览




文档简介
4.5多边形和圆的初步认识
2. 我们经常见到的一些图形:
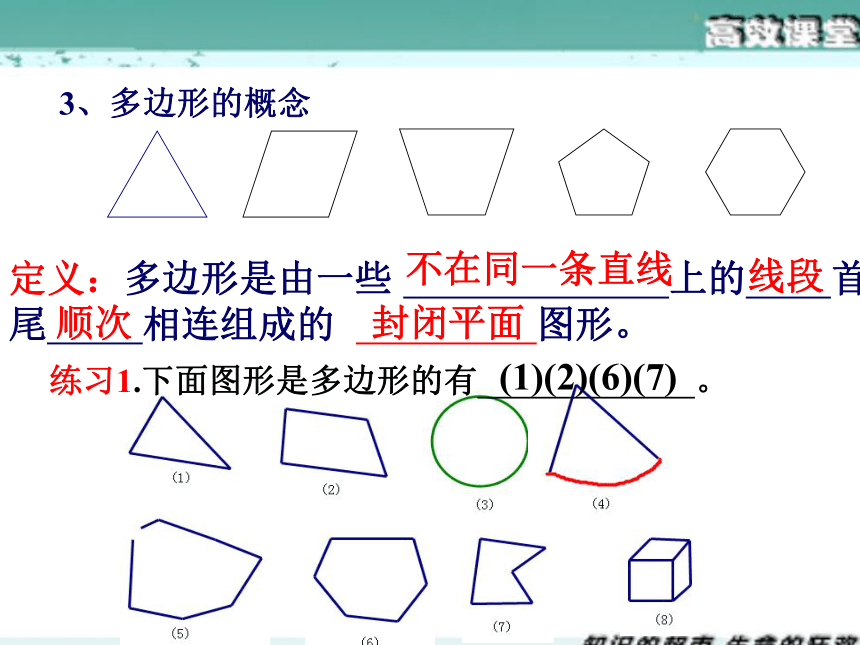
3、多边形的概念
定义:多边形是由一些 上的 首尾 相连组成的 图形。
不在同一条直线
线段
顺次
封闭平面
练习1.下面图形是多边形的有 。
(1)(2)(6)(7)
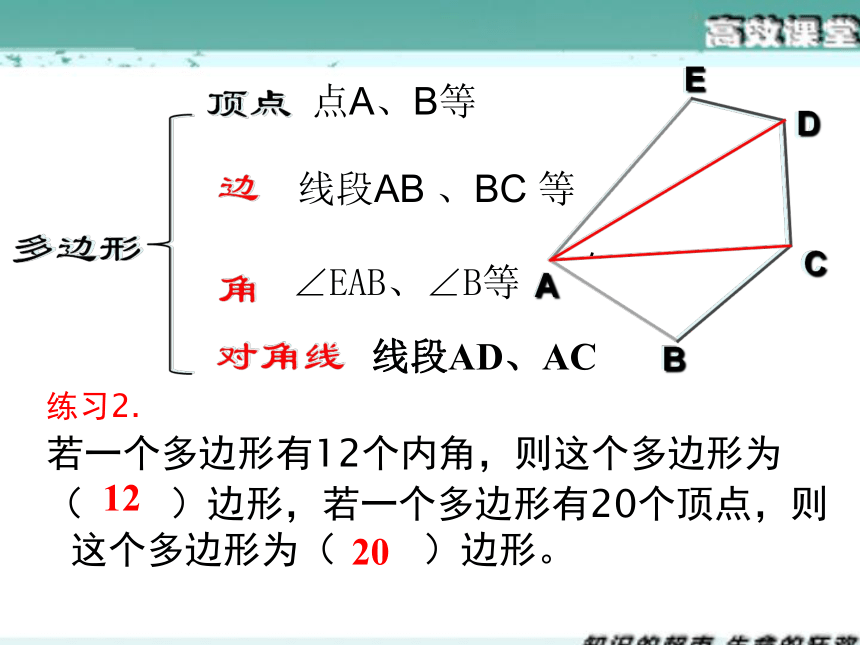
练习2.
若一个多边形有12个内角,则这个多边形为
( )边形,若一个多边形有20个顶点,则这个多边形为( )边形。
12
20
点A、B等
线段AB 、BC 等
∠EAB、∠B等
线段AD、AC
观察下图中的多边形,它们的边和角有什么特点?
各边相等,各角也相等的多边形叫做正多边形。
练习3.判断
(1)各边都相等的多边形为正多边形。
(2)各个内角都相等的多边形为正多边形。
(×)
(×)
…
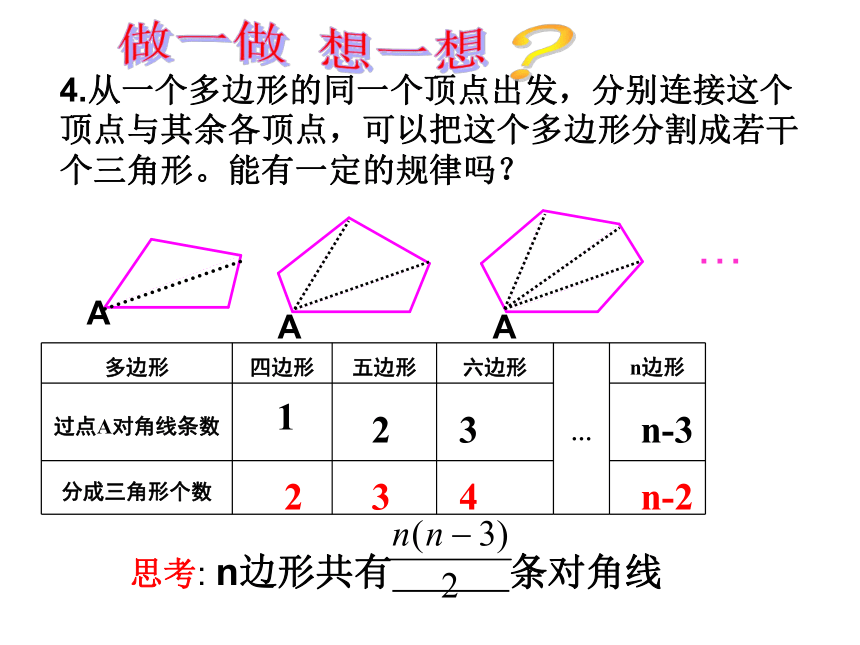
4.从一个多边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形。能有一定的规律吗?
思考: n边形共有 条对角线
多边形
四边形
五边形
六边形
…
n边形
过点A对角线条数
分成三角形个数
A
1
2
3
2
3
4
n-3
n-2
A
A
1、从一个十八边形的某个顶点出发,分别连结这个点与其余各顶点,可以把这个十八边形分割成几个三角形?
2、从一个多边形的某个顶点出发,分别连结这个点与其余各顶点,把这个多边形分割成10个三角形,这是几边形?
18-2=16
答:可以把这个十八边形分割成16个三角形。
12个
如果从一个多边形内部的任意一点出发,分别连接这个点与其余各顶点,可以把这个多边形分割成若干个三角形。你能看出什么规律吗?
4个
5个
6个
N边形
N个
如果从一个多边形的边上除顶点外的任意一点出发,分别连接这个点与其余各顶点,可以把这个多边形分割成若干个三角形。你能看出什么规律吗?
N边形
3个
4个
5个
N-1个
B
A
绳子扫过的区域是什么形状?
议一议
O
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆(circle).固定的端点O称为圆心(center of a circle),线段OA称为半径(radius).
A
O
B
圆的有关概念
圆上A,B两点之间的部分叫做圆弧(arc)。
A
O
由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形(sector).顶点在圆心的角叫做圆心角。
圆可以分割成若干个扇形。
O
A
C
B
如图,若OA,OB,OC是圆的三条半径,则图中共有 个扇形。
例:将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,求这三个扇形的圆心角的度数。
解:因为一个周角为 ,所以分成的三个扇形的圆心角分别为:
O
B
C
A
(1)将一个圆形的蛋糕分成大小相等的
六块,你能算出每一块的圆心角的度数吗?
你知道每一块的面积与整个圆的面积的关系吗?
(2)如果这个蛋糕的半
径为10cm,那么一块
蛋糕的面积是多大?
我能行:以两个圆.两个三角形.两条线段为构件,尽可能多地构思独特且具有意义的图形,并写上一两句贴切.诙谐的解说词,如:
和尚打伞无法(发)无天
奥运健儿再创辉煌
一把小雨伞
一个和尚
做一做随堂练习
你的能力怎么样?
1.平面图形是由同一个平面内的点、线构成的图形。
2.多边形及多边形的特征——由一些不在同一条直
线上的线段依次首尾相连组成的封闭图形。
点滴归纳,条理清晰
3.平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆(circle).固定的端点O称为圆心(center of a circle),线段OA称为半径(radius).
4.圆上A,B两点之间的部分叫做圆弧(arc),
5.由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形(sector).定点在圆心的角叫做圆心角
作业:
A组:习题4.5(P125)的1、2题,P126的3、4、5、6.
B组:习题4.5(P125)的第2题,P126的3、4、5、6.
谈一谈自己的感受!
1.经历从现实世界中抽象出平面图形的过程,并能用美丽的图形打扮世界。
2.在具体的情境中认识多边形、圆、扇形、弧。
3.在丰富的活动中发展有条理的思考,能从图形的变化中找出不变的规律。
2. 我们经常见到的一些图形:
3、多边形的概念
定义:多边形是由一些 上的 首尾 相连组成的 图形。
不在同一条直线
线段
顺次
封闭平面
练习1.下面图形是多边形的有 。
(1)(2)(6)(7)
练习2.
若一个多边形有12个内角,则这个多边形为
( )边形,若一个多边形有20个顶点,则这个多边形为( )边形。
12
20
点A、B等
线段AB 、BC 等
∠EAB、∠B等
线段AD、AC
观察下图中的多边形,它们的边和角有什么特点?
各边相等,各角也相等的多边形叫做正多边形。
练习3.判断
(1)各边都相等的多边形为正多边形。
(2)各个内角都相等的多边形为正多边形。
(×)
(×)
…
4.从一个多边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形。能有一定的规律吗?
思考: n边形共有 条对角线
多边形
四边形
五边形
六边形
…
n边形
过点A对角线条数
分成三角形个数
A
1
2
3
2
3
4
n-3
n-2
A
A
1、从一个十八边形的某个顶点出发,分别连结这个点与其余各顶点,可以把这个十八边形分割成几个三角形?
2、从一个多边形的某个顶点出发,分别连结这个点与其余各顶点,把这个多边形分割成10个三角形,这是几边形?
18-2=16
答:可以把这个十八边形分割成16个三角形。
12个
如果从一个多边形内部的任意一点出发,分别连接这个点与其余各顶点,可以把这个多边形分割成若干个三角形。你能看出什么规律吗?
4个
5个
6个
N边形
N个
如果从一个多边形的边上除顶点外的任意一点出发,分别连接这个点与其余各顶点,可以把这个多边形分割成若干个三角形。你能看出什么规律吗?
N边形
3个
4个
5个
N-1个
B
A
绳子扫过的区域是什么形状?
议一议
O
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆(circle).固定的端点O称为圆心(center of a circle),线段OA称为半径(radius).
A
O
B
圆的有关概念
圆上A,B两点之间的部分叫做圆弧(arc)。
A
O
由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形(sector).顶点在圆心的角叫做圆心角。
圆可以分割成若干个扇形。
O
A
C
B
如图,若OA,OB,OC是圆的三条半径,则图中共有 个扇形。
例:将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,求这三个扇形的圆心角的度数。
解:因为一个周角为 ,所以分成的三个扇形的圆心角分别为:
O
B
C
A
(1)将一个圆形的蛋糕分成大小相等的
六块,你能算出每一块的圆心角的度数吗?
你知道每一块的面积与整个圆的面积的关系吗?
(2)如果这个蛋糕的半
径为10cm,那么一块
蛋糕的面积是多大?
我能行:以两个圆.两个三角形.两条线段为构件,尽可能多地构思独特且具有意义的图形,并写上一两句贴切.诙谐的解说词,如:
和尚打伞无法(发)无天
奥运健儿再创辉煌
一把小雨伞
一个和尚
做一做随堂练习
你的能力怎么样?
1.平面图形是由同一个平面内的点、线构成的图形。
2.多边形及多边形的特征——由一些不在同一条直
线上的线段依次首尾相连组成的封闭图形。
点滴归纳,条理清晰
3.平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆(circle).固定的端点O称为圆心(center of a circle),线段OA称为半径(radius).
4.圆上A,B两点之间的部分叫做圆弧(arc),
5.由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形(sector).定点在圆心的角叫做圆心角
作业:
A组:习题4.5(P125)的1、2题,P126的3、4、5、6.
B组:习题4.5(P125)的第2题,P126的3、4、5、6.
谈一谈自己的感受!
1.经历从现实世界中抽象出平面图形的过程,并能用美丽的图形打扮世界。
2.在具体的情境中认识多边形、圆、扇形、弧。
3.在丰富的活动中发展有条理的思考,能从图形的变化中找出不变的规律。
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
