人教版七年级数学下册 5.2 平行线及其判定 练习题(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.2 平行线及其判定 练习题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 565.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览

文档简介
人教版七年级数学下册
第五章
相交线与平行线
5.2
平行线及其判定
练习题
一、选择题
1.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于(
)时,AB∥CD.
A.50°
B.40°
C.30°
D.60°
2.有以下3个说法:①垂线相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行.其中错误说法的个数是(
)
A.0个
B.1个
C.2个
D.3个
3.如图,下列说法中,正确的是(
)
A.因为∠A+∠D=180°,所以AD∥BC
B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD
D.因为∠A+∠C=180°,所以AB∥CD
4.下列说法正确的是(
)
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面没有公共点的两条射线平行
5.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是(
)
A.平行
B.相交
C.重合
D.以上都有可能
6.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
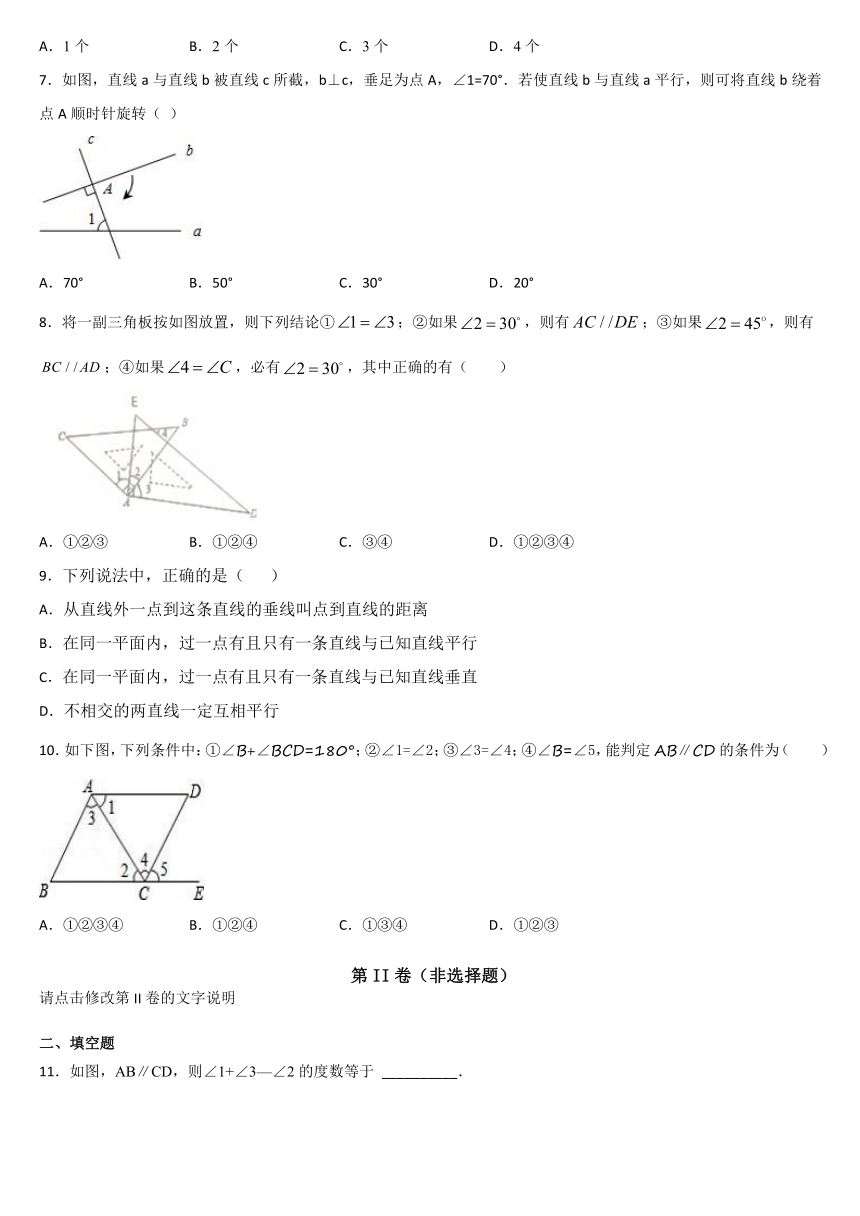
7.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转(
)
A.70°
B.50°
C.30°
D.20°
8.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有(
)
A.①②③
B.①②④
C.③④
D.①②③④
9.下列说法中,正确的是(
)
A.从直线外一点到这条直线的垂线叫点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线平行
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.不相交的两直线一定互相平行
10.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④
B.①②④
C.①③④
D.①②③
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,AB∥CD,则∠1+∠3—∠2的度数等于
__________.
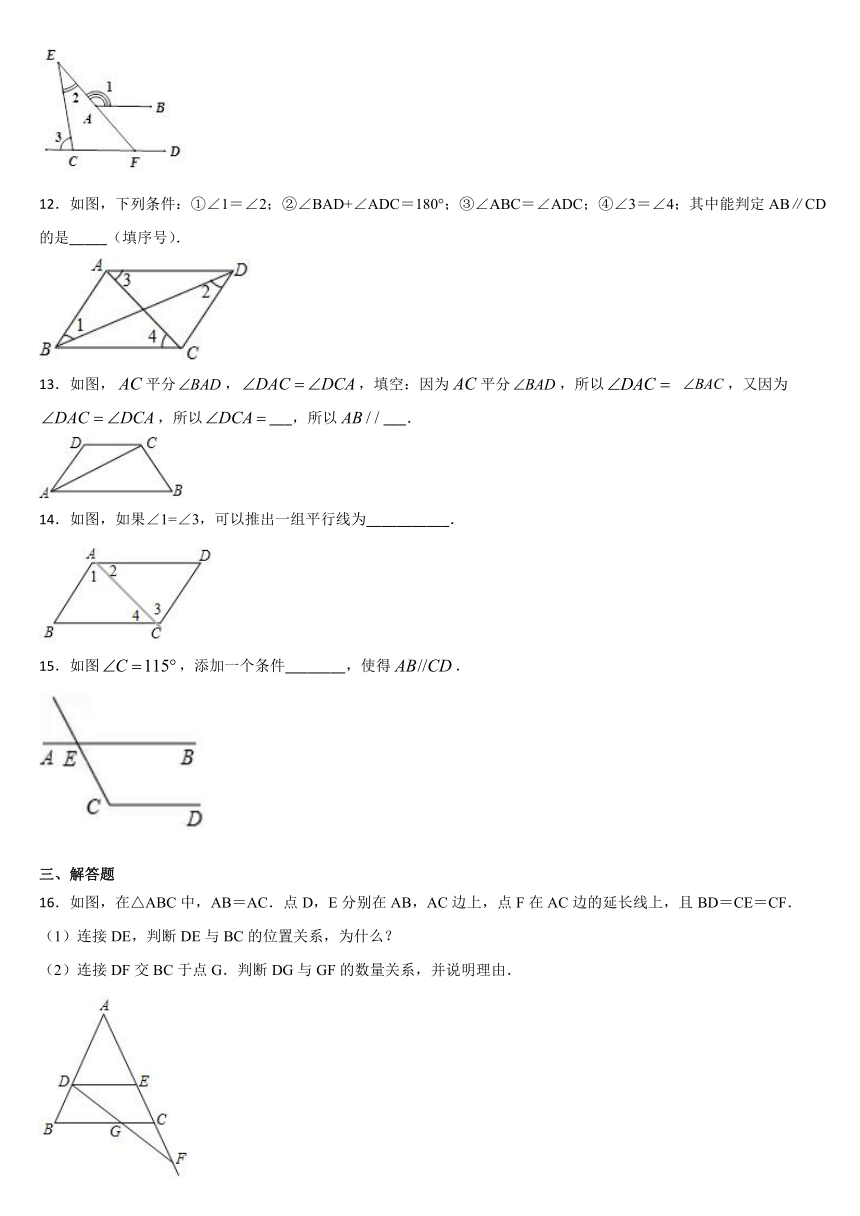
12.如图,下列条件:①∠1=∠2;②∠BAD+∠ADC=180°;③∠ABC=∠ADC;④∠3=∠4;其中能判定AB∥CD的是_____(填序号).
13.如图,平分,,填空:因为平分,所以
,又因为,所以___,所以___.
14.如图,如果∠1=∠3,可以推出一组平行线为___________.
15.如图,添加一个条件________,使得.
三、解答题
16.如图,在△ABC中,AB=AC.点D,E分别在AB,AC边上,点F在AC边的延长线上,且BD=CE=CF.
(1)连接DE,判断DE与BC的位置关系,为什么?
(2)连接DF交BC于点G.判断DG与GF的数量关系,并说明理由.
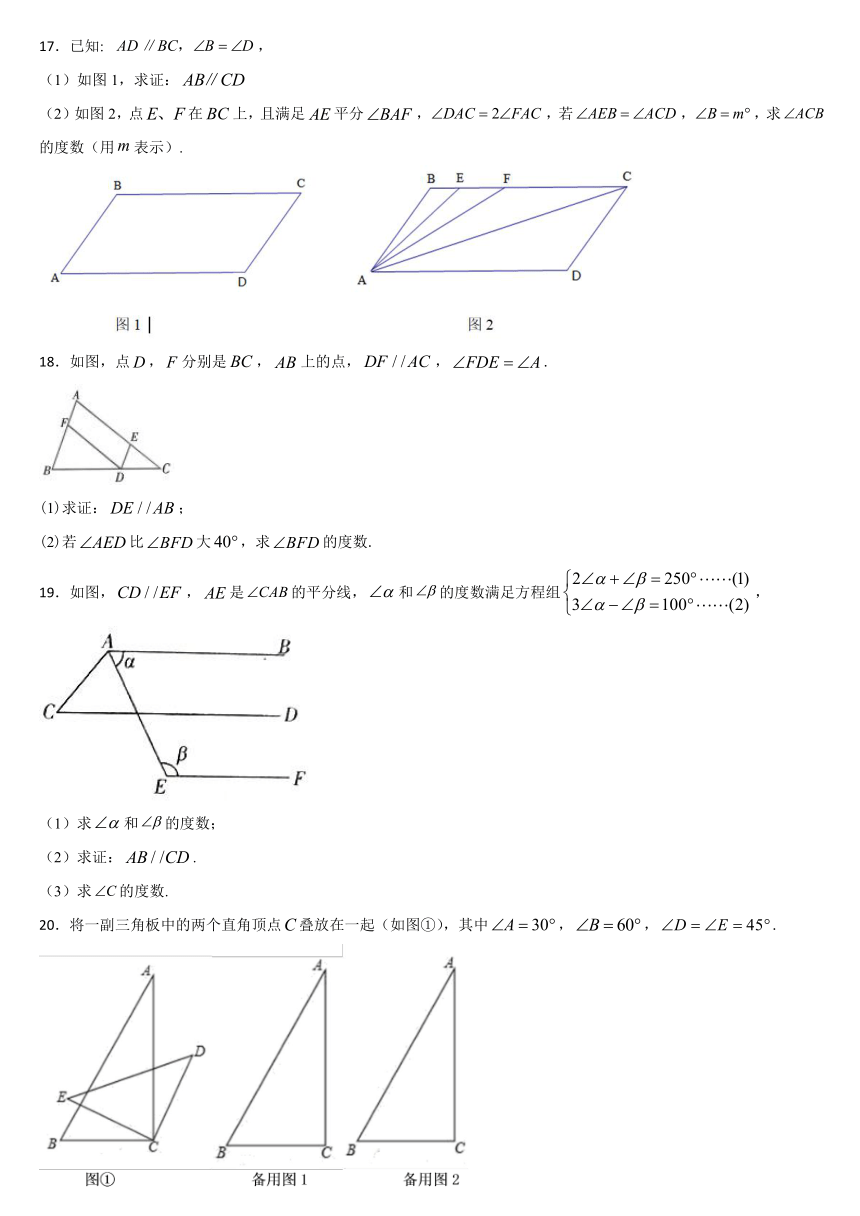
17.已知:
,
(1)如图1,求证:
(2)如图2,点在上,且满足平分,,若,,求的度数(用表示).
18.如图,点,分别是,上的点,,.
(1)求证:;
(2)若比大,求的度数.
19.如图,,是的平分线,和的度数满足方程组,
(1)求和的度数;
(2)求证:.
(3)求的度数.
20.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
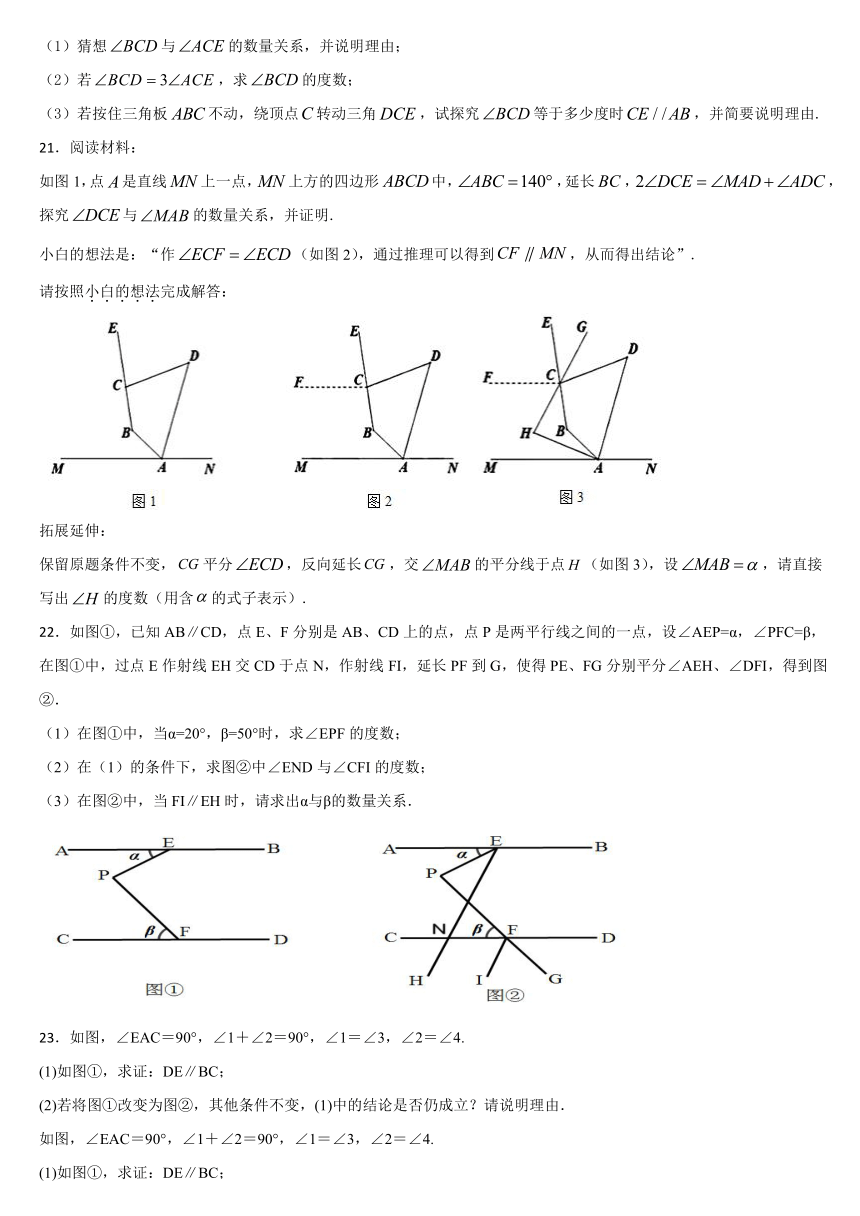
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
21.阅读材料:
如图1,点是直线上一点,上方的四边形中,,延长,,探究与的数量关系,并证明.
小白的想法是:“作(如图2),通过推理可以得到,从而得出结论”.
请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,平分,反向延长,交的平分线于点(如图3),设,请直接写出的度数(用含的式子表示).
22.如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
23.如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
【参考答案】
1.A
2.D
3.C
4.C
5.B
6.B
7.D
8.D
9.C
10.C
11.180°
12.①②.
13.
DC
14.AB//CD
15.或∠AEC=115°
16.解:(1)结论:DE∥BC.
理由:∵AB=AC,
∴∠B=∠ACB,
∵BD=EC,
∴AD=AE,
∴∠ADE=∠AED,
∵∠A+2∠ADE=180°,∠A+2∠B=180°,
∴∠ADE=∠B,
∴DE∥BC.
(2)结论:DG=GF.
理由:∵CG∥DE,EC=CF,
∴DG=GC.
17.解:(1)∵AD∥BC,
∴∠A+∠B=180°,
∵∠B=∠D,
∴∠A+∠D=180°,
∴AB∥CD;
(2)∵∠B=∠D,,
又∵∠BAE=,∠DAC=,
∴∠BAE=∠DAC,
∵AD∥BC,平分,
∴∠DAC=∠ACB,∠BAE=∠EAF,
即∠BAE=∠EAF=∠DAC=∠ACB,
∵,
∴,
∴∠BAD=∠BAE+∠EAF+∠FAC+∠DAC=∠ACB,
∵∠B+∠BAD=180°,,
∴
∴.
18.(1)证明:
(2)解:
19.解:(1)①②,得,
,代入①得
和的度数分别为和.
(2)
,
(3)是的平分线
,
20.解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
21.解:【阅读材料】
作,,(如图1).
∵,
∴.
∴.
∵,
∴.
∴.
∴.
∵,
∴.
∵,
∴.
∴,.
∴.
∵,
∴.
【拓展延伸】
结论:.
理由:如图,作,过H点作HP∥MN,
∴∠PHA=∠MAH=,
由(1)得FC∥MN,
∴FC∥HP,
∴∠PHC=∠FCH,
∵,CG平分∠ECD,
∴∠ECG=20°+,
∴∠FCH=
=180°-()-(20°+)
=120°-
∴∠CHA=∠PHA+∠PHC=+(120°-)=120°-
即:.
22.(1)∵PM∥AB,α=20°,
∴∠EPM=∠AEP=20°,
∵AB∥CD,PM∥AB,
∴PM∥CD,
∴∠MPF=∠CFP=50°,
∴∠EPF=20°+50°=70°;
(2)∵PE平分∠AEH,
∴∠AEH=2α=40°,
∵AD∥BC,
∴∠END=∠AEH=40°,
又∵FG平分∠DFI,
∴∠IFG=∠DFG=β=50°,
∴∠CFI=180°-2β=80°;
(3)由(2)可得,∠CFI=180°-2β,
∵AB∥CD,
∴∠END=∠AEN=2α,
∴当FI∥EH时,∠END=∠CFI,
即2α=180°-2β,
∴α+β=90°.
23.(1)用三角形的内角和定理判断∠D+∠B=180°;(2)连接EC,证明∠AEC+∠ACE+∠3+∠4=180°,根据同旁内角互补,两直线平行证明.
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
第五章
相交线与平行线
5.2
平行线及其判定
练习题
一、选择题
1.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于(
)时,AB∥CD.
A.50°
B.40°
C.30°
D.60°
2.有以下3个说法:①垂线相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行.其中错误说法的个数是(
)
A.0个
B.1个
C.2个
D.3个
3.如图,下列说法中,正确的是(
)
A.因为∠A+∠D=180°,所以AD∥BC
B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD
D.因为∠A+∠C=180°,所以AB∥CD
4.下列说法正确的是(
)
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面没有公共点的两条射线平行
5.在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是(
)
A.平行
B.相交
C.重合
D.以上都有可能
6.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转(
)
A.70°
B.50°
C.30°
D.20°
8.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有(
)
A.①②③
B.①②④
C.③④
D.①②③④
9.下列说法中,正确的是(
)
A.从直线外一点到这条直线的垂线叫点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线平行
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.不相交的两直线一定互相平行
10.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④
B.①②④
C.①③④
D.①②③
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,AB∥CD,则∠1+∠3—∠2的度数等于
__________.
12.如图,下列条件:①∠1=∠2;②∠BAD+∠ADC=180°;③∠ABC=∠ADC;④∠3=∠4;其中能判定AB∥CD的是_____(填序号).
13.如图,平分,,填空:因为平分,所以
,又因为,所以___,所以___.
14.如图,如果∠1=∠3,可以推出一组平行线为___________.
15.如图,添加一个条件________,使得.
三、解答题
16.如图,在△ABC中,AB=AC.点D,E分别在AB,AC边上,点F在AC边的延长线上,且BD=CE=CF.
(1)连接DE,判断DE与BC的位置关系,为什么?
(2)连接DF交BC于点G.判断DG与GF的数量关系,并说明理由.
17.已知:
,
(1)如图1,求证:
(2)如图2,点在上,且满足平分,,若,,求的度数(用表示).
18.如图,点,分别是,上的点,,.
(1)求证:;
(2)若比大,求的度数.
19.如图,,是的平分线,和的度数满足方程组,
(1)求和的度数;
(2)求证:.
(3)求的度数.
20.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
21.阅读材料:
如图1,点是直线上一点,上方的四边形中,,延长,,探究与的数量关系,并证明.
小白的想法是:“作(如图2),通过推理可以得到,从而得出结论”.
请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,平分,反向延长,交的平分线于点(如图3),设,请直接写出的度数(用含的式子表示).
22.如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
23.如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
【参考答案】
1.A
2.D
3.C
4.C
5.B
6.B
7.D
8.D
9.C
10.C
11.180°
12.①②.
13.
DC
14.AB//CD
15.或∠AEC=115°
16.解:(1)结论:DE∥BC.
理由:∵AB=AC,
∴∠B=∠ACB,
∵BD=EC,
∴AD=AE,
∴∠ADE=∠AED,
∵∠A+2∠ADE=180°,∠A+2∠B=180°,
∴∠ADE=∠B,
∴DE∥BC.
(2)结论:DG=GF.
理由:∵CG∥DE,EC=CF,
∴DG=GC.
17.解:(1)∵AD∥BC,
∴∠A+∠B=180°,
∵∠B=∠D,
∴∠A+∠D=180°,
∴AB∥CD;
(2)∵∠B=∠D,,
又∵∠BAE=,∠DAC=,
∴∠BAE=∠DAC,
∵AD∥BC,平分,
∴∠DAC=∠ACB,∠BAE=∠EAF,
即∠BAE=∠EAF=∠DAC=∠ACB,
∵,
∴,
∴∠BAD=∠BAE+∠EAF+∠FAC+∠DAC=∠ACB,
∵∠B+∠BAD=180°,,
∴
∴.
18.(1)证明:
(2)解:
19.解:(1)①②,得,
,代入①得
和的度数分别为和.
(2)
,
(3)是的平分线
,
20.解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
21.解:【阅读材料】
作,,(如图1).
∵,
∴.
∴.
∵,
∴.
∴.
∴.
∵,
∴.
∵,
∴.
∴,.
∴.
∵,
∴.
【拓展延伸】
结论:.
理由:如图,作,过H点作HP∥MN,
∴∠PHA=∠MAH=,
由(1)得FC∥MN,
∴FC∥HP,
∴∠PHC=∠FCH,
∵,CG平分∠ECD,
∴∠ECG=20°+,
∴∠FCH=
=180°-()-(20°+)
=120°-
∴∠CHA=∠PHA+∠PHC=+(120°-)=120°-
即:.
22.(1)∵PM∥AB,α=20°,
∴∠EPM=∠AEP=20°,
∵AB∥CD,PM∥AB,
∴PM∥CD,
∴∠MPF=∠CFP=50°,
∴∠EPF=20°+50°=70°;
(2)∵PE平分∠AEH,
∴∠AEH=2α=40°,
∵AD∥BC,
∴∠END=∠AEH=40°,
又∵FG平分∠DFI,
∴∠IFG=∠DFG=β=50°,
∴∠CFI=180°-2β=80°;
(3)由(2)可得,∠CFI=180°-2β,
∵AB∥CD,
∴∠END=∠AEN=2α,
∴当FI∥EH时,∠END=∠CFI,
即2α=180°-2β,
∴α+β=90°.
23.(1)用三角形的内角和定理判断∠D+∠B=180°;(2)连接EC,证明∠AEC+∠ACE+∠3+∠4=180°,根据同旁内角互补,两直线平行证明.
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
