高中数学人教A版(2019)选择性必修第一册第一章1.2空间向量基本定理(2)-课件(共19张PPY)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.2空间向量基本定理(2)-课件(共19张PPY) |

|
|
| 格式 | pptx | ||
| 文件大小 | 522.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览







文档简介
空间向量基本定理(2)
问题1 你能用自己的语言复述空间向量基本定理吗?
空间向量基本定理
我们把{a,b,c}叫做空间的一个基底(base),a,b,c 都叫做基向量(base vectors) .
如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
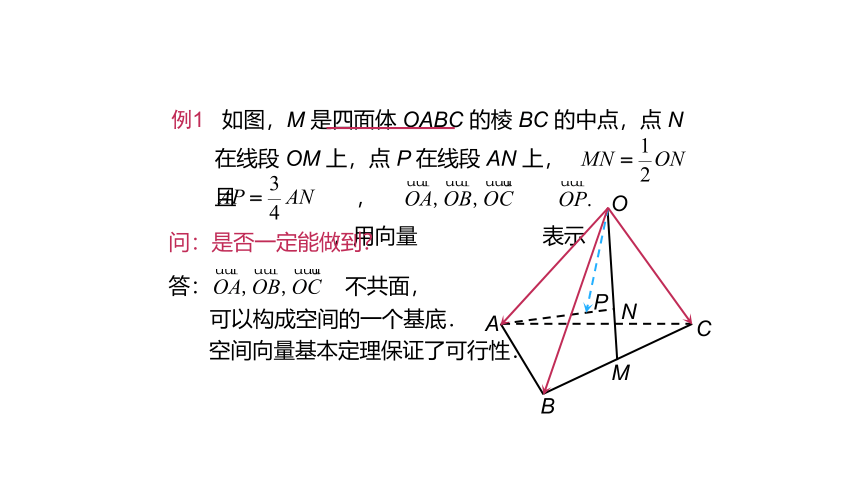
例1 如图,M 是四面体 OABC 的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 ,
,用向量 表示
问:是否一定能做到?
答: 不共面,
空间向量基本定理保证了可行性.
可以构成空间的一个基底.
O
A
B
C
M
N
P
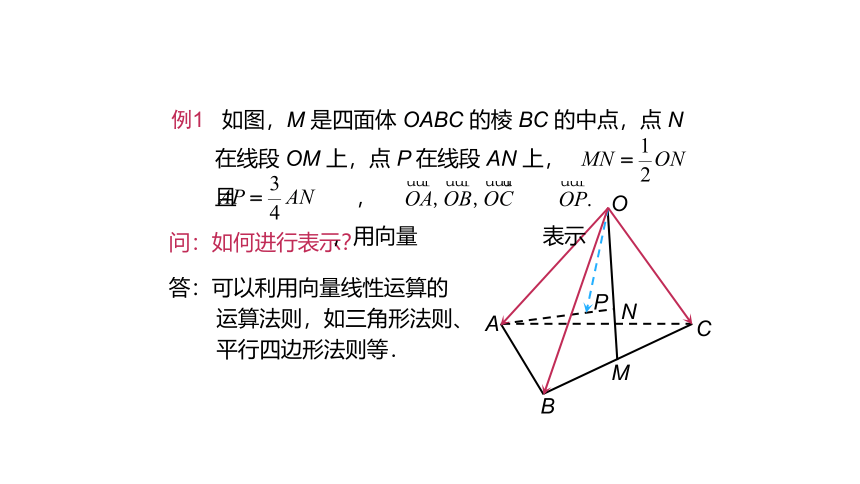
答:可以利用向量线性运算的
运算法则,如三角形法则、
平行四边形法则等.
问:如何进行表示?
O
A
B
C
M
N
P
例1 如图,M 是四面体 OABC 的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 ,
,用向量 表示
解:
O
A
B
C
M
N
P
Q
问题2 通过这道例题的解题过程,同学们能否总结出用基向量表示空间向量的方法呢?
结合图形特征,利用三角形法则、平行四边形法则、向量数乘等线性运算法则,将待求向量逐步转化为基向量,将未知化归为已知.
用基向量表示空间向量的方法
答:综合几何方法:
问:证明异面直线垂直,你能想到
哪些方法?
向量方法.
证明异面直线所成角为直角;
线面垂直的定义和性质等.
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
答:可以转化为向量问题
问:如何使用向量方法解决立体几何
问题?
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
答:可以转化为向量问题
问:如何使用向量方法解决立体几何
问题?
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
求证
只需证
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
问:如何计算 ?
向已知条件转化.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
证明:
设
这三个向量不共面,{a,b,c}是空间的一个基底.
则
所以
所以
所以
选取基底(不共面且已知长度夹角)
4
A
B
C
D
A1
B1
C1
D1
M
N
4
5
用基向量表示相关向量
还原为几何问题的解
把相关向量的运算转化为基向量的运算
向量问题的解
选取基底(不共面且已知长度夹角)
证明:
设
这三个向量不共面,{a,b,c}是空间的一个基底.
则
所以
所以
所以
选取基底(不共面且已知长度夹角)
立体几何问题
用向量方法解决立体几何问题的路径
①适当选取基底
向量
运算
转化
②用基向量表示相关向量
③将相关向量的问题转化为基向量的问题
向量问题
向量问题的解
立体几何问题的解
转化
向量方法
理论基础:空间向量基本定理
答:可以取单位正交基底.
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
问:单位正方体这个条件对解题
有什么作用?
单位:基向量长度为1.
正交:基向量两两垂直,
A
B
C
D
A'
B'
C'
D'
E
F
G
任意两不同基向量数量积为0.
问:如何用向量方法证明EF//AC?
答:只需证 ,
只需证存在实数 λ,
使得 .
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
A
B
C
D
A'
B'
C'
D'
E
F
G
证明:
设
则 {i,j,k} 构成空间的一个单位正交基底.
所以
所以
所以
所以
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
问:如何用向量表示 CE 与 AG 所 成角的余弦值?
答:求 与 所成角的余弦值.
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
(2)求 CE 与 AG 所成角
的余弦值.
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
解:
因为
所以
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
所以 CE 与 AG 所成角的余弦值为
1
0
0
0
选取单位正交基底
有利于运算
解:
因为
所以
思考:是否可以用 与 所
成角的余弦值来求解第2小问?
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
(2)求 CE 与 AG 所成角
的余弦值.
A
B
C
D
A'
B'
C'
D'
E
F
G
应用一个定理:空间向量基本定理
学习一种方法:向量方法
体会一种思想:转化与化归思想
课堂小结
课后作业
1. 如图,在棱长为1的正方体 ABCD-A1B1C1D1中,E,F 分别为DD1,BD的中点,点 G 在 CD 上,且
(1)求证:EF⊥B1C ;
(2)求 EF 与 C1G 所成角的余弦值.
(思考题)用综合几何方法证明或求解例
题,体会综合几何方法与向量方法的特点.
问题1 你能用自己的语言复述空间向量基本定理吗?
空间向量基本定理
我们把{a,b,c}叫做空间的一个基底(base),a,b,c 都叫做基向量(base vectors) .
如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
例1 如图,M 是四面体 OABC 的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 ,
,用向量 表示
问:是否一定能做到?
答: 不共面,
空间向量基本定理保证了可行性.
可以构成空间的一个基底.
O
A
B
C
M
N
P
答:可以利用向量线性运算的
运算法则,如三角形法则、
平行四边形法则等.
问:如何进行表示?
O
A
B
C
M
N
P
例1 如图,M 是四面体 OABC 的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 ,
,用向量 表示
解:
O
A
B
C
M
N
P
Q
问题2 通过这道例题的解题过程,同学们能否总结出用基向量表示空间向量的方法呢?
结合图形特征,利用三角形法则、平行四边形法则、向量数乘等线性运算法则,将待求向量逐步转化为基向量,将未知化归为已知.
用基向量表示空间向量的方法
答:综合几何方法:
问:证明异面直线垂直,你能想到
哪些方法?
向量方法.
证明异面直线所成角为直角;
线面垂直的定义和性质等.
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
答:可以转化为向量问题
问:如何使用向量方法解决立体几何
问题?
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
答:可以转化为向量问题
问:如何使用向量方法解决立体几何
问题?
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
求证
只需证
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
例2 如图,在平行六面体 ABCD-A1B1C1D1中,AB=4,AD=4, AA1=5,∠DAB=60°,∠BAA1=60 ° ,∠DAA1=60 ° ,M,N 分别为D1C1,C1B1的中点.
求证 MN⊥AC1.
问:如何计算 ?
向已知条件转化.
A
B
C
D
A1
B1
C1
D1
M
N
4
5
4
证明:
设
这三个向量不共面,{a,b,c}是空间的一个基底.
则
所以
所以
所以
选取基底(不共面且已知长度夹角)
4
A
B
C
D
A1
B1
C1
D1
M
N
4
5
用基向量表示相关向量
还原为几何问题的解
把相关向量的运算转化为基向量的运算
向量问题的解
选取基底(不共面且已知长度夹角)
证明:
设
这三个向量不共面,{a,b,c}是空间的一个基底.
则
所以
所以
所以
选取基底(不共面且已知长度夹角)
立体几何问题
用向量方法解决立体几何问题的路径
①适当选取基底
向量
运算
转化
②用基向量表示相关向量
③将相关向量的问题转化为基向量的问题
向量问题
向量问题的解
立体几何问题的解
转化
向量方法
理论基础:空间向量基本定理
答:可以取单位正交基底.
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
问:单位正方体这个条件对解题
有什么作用?
单位:基向量长度为1.
正交:基向量两两垂直,
A
B
C
D
A'
B'
C'
D'
E
F
G
任意两不同基向量数量积为0.
问:如何用向量方法证明EF//AC?
答:只需证 ,
只需证存在实数 λ,
使得 .
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
A
B
C
D
A'
B'
C'
D'
E
F
G
证明:
设
则 {i,j,k} 构成空间的一个单位正交基底.
所以
所以
所以
所以
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
问:如何用向量表示 CE 与 AG 所 成角的余弦值?
答:求 与 所成角的余弦值.
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
(2)求 CE 与 AG 所成角
的余弦值.
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
解:
因为
所以
A
B
C
D
A'
B'
C'
D'
E
F
G
i
j
k
所以 CE 与 AG 所成角的余弦值为
1
0
0
0
选取单位正交基底
有利于运算
解:
因为
所以
思考:是否可以用 与 所
成角的余弦值来求解第2小问?
例3 如图,正方体 ABCD-A'B'C'D'的棱长为1,E,F, G分别为C'D', A'D', D'D的中点.
(1)求证:EF∥AC ;
(2)求 CE 与 AG 所成角
的余弦值.
A
B
C
D
A'
B'
C'
D'
E
F
G
应用一个定理:空间向量基本定理
学习一种方法:向量方法
体会一种思想:转化与化归思想
课堂小结
课后作业
1. 如图,在棱长为1的正方体 ABCD-A1B1C1D1中,E,F 分别为DD1,BD的中点,点 G 在 CD 上,且
(1)求证:EF⊥B1C ;
(2)求 EF 与 C1G 所成角的余弦值.
(思考题)用综合几何方法证明或求解例
题,体会综合几何方法与向量方法的特点.
