高中数学人教A版(2019)选择性必修第一册第一章1.4.1用空间向量研究直线、平面的位置关系(2)-课件(共17张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.4.1用空间向量研究直线、平面的位置关系(2)-课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 980.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览

文档简介
用空间向量研究直线、平面的
位置关系(2)
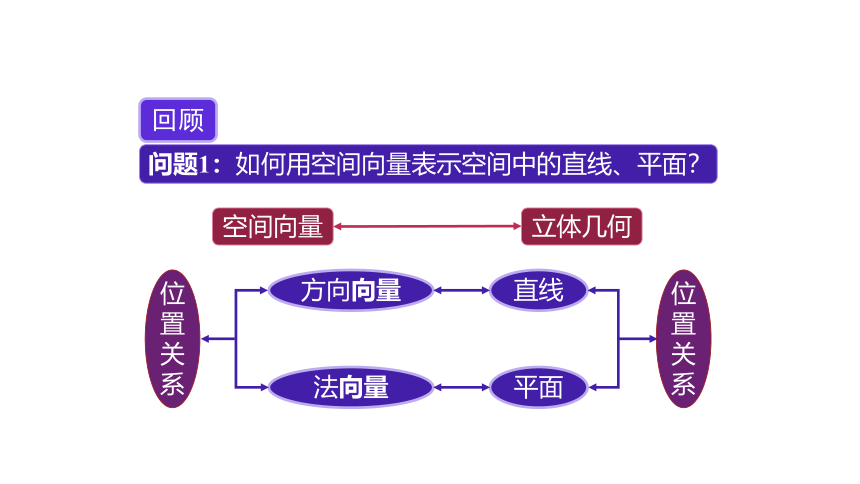
回顾
直线
平面
方向向量
法向量
位置关系
位置关系
立体几何
空间向量
问题1:如何用空间向量表示空间中的直线、平面?
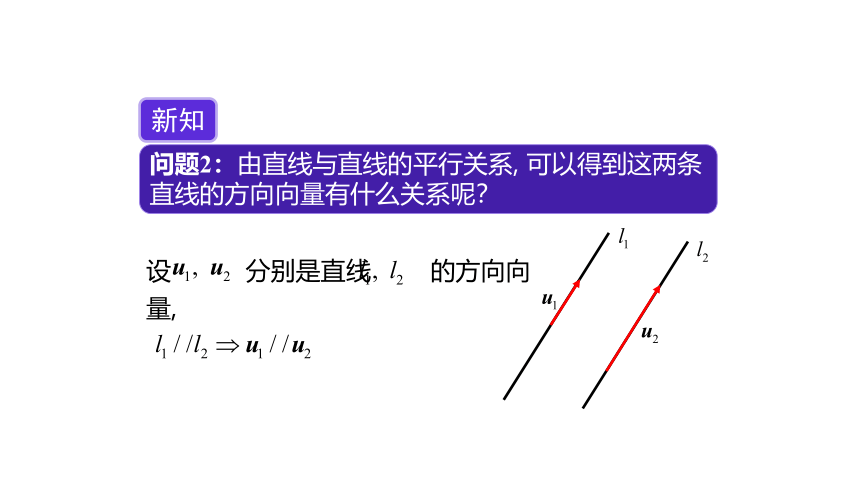
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
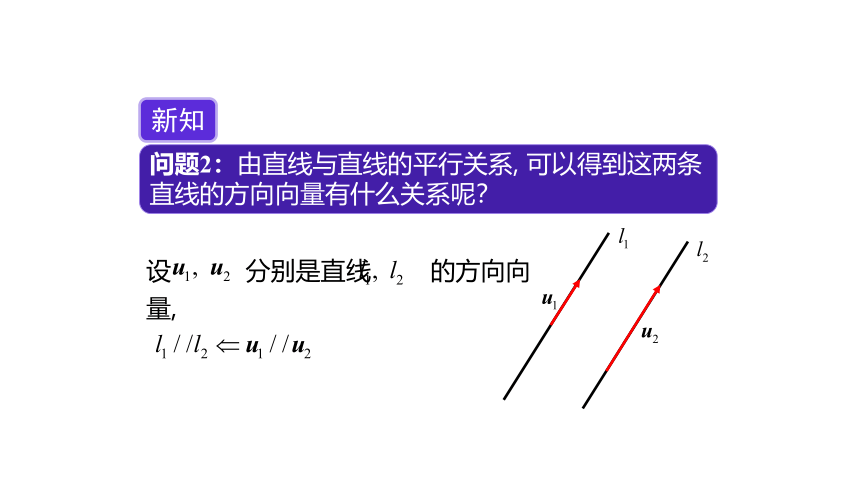
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
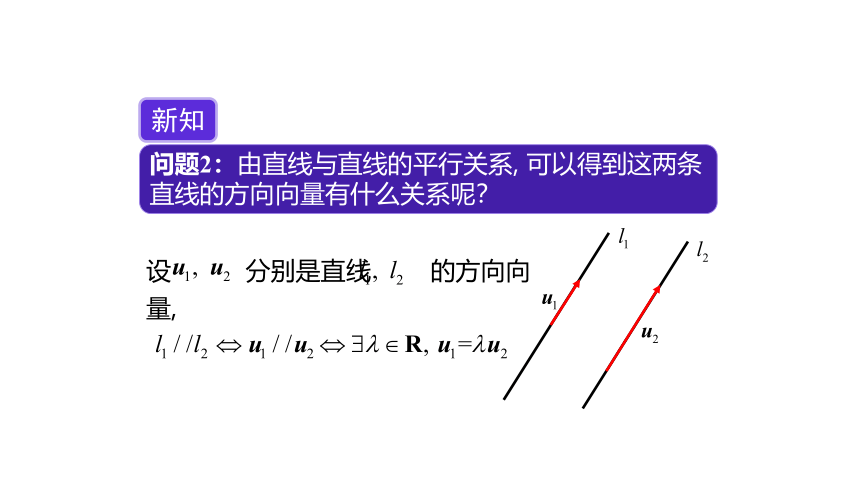
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
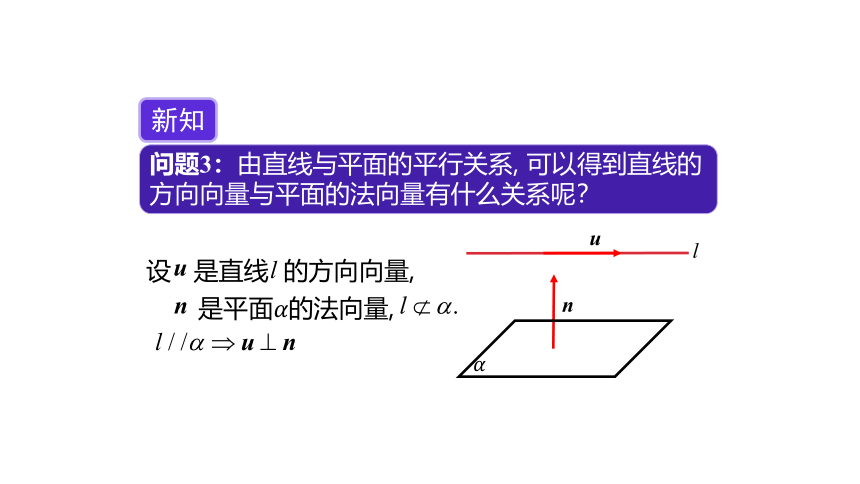
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
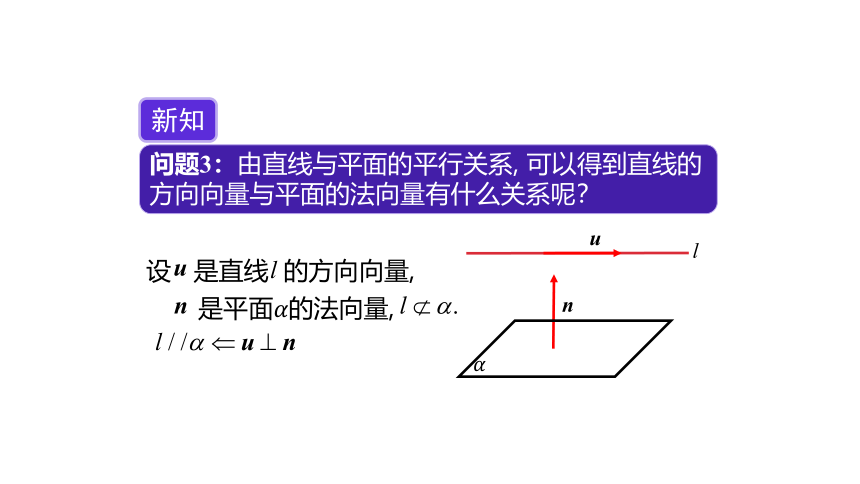
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
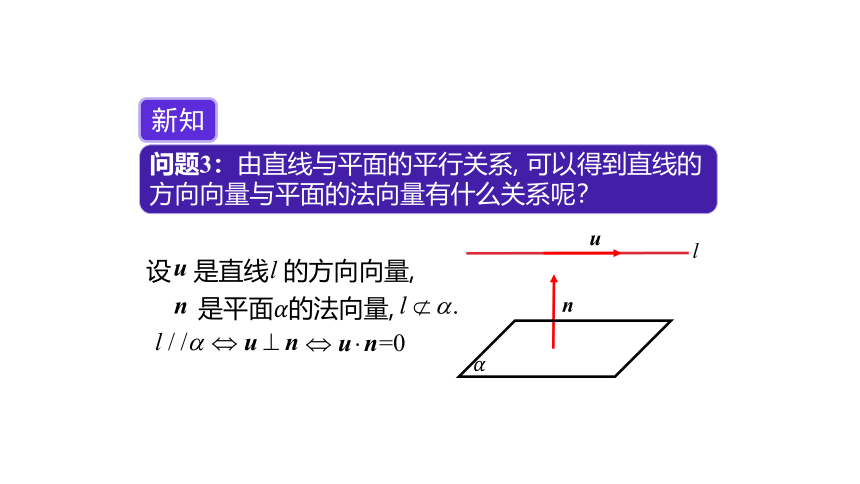
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
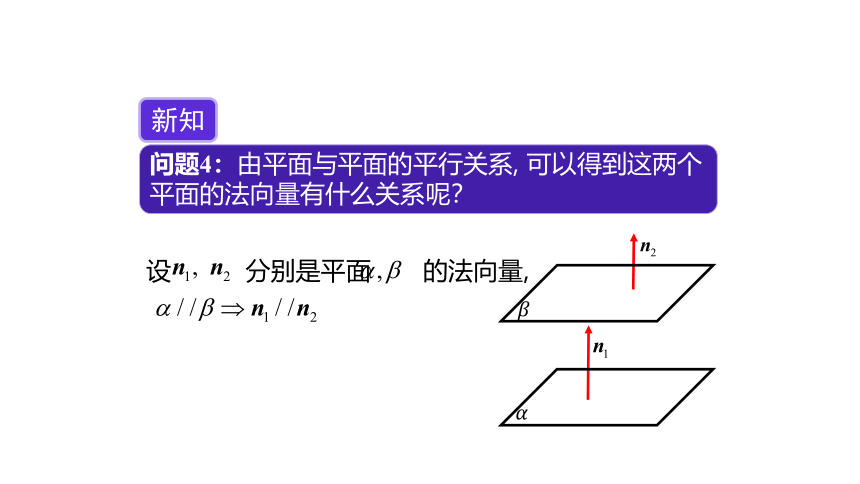
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行, 则这两个平面平行.
例题
????
?
已知:如图,
求证: .
????
?
a
b
P
已知:如图,
求证: .
分析:
平面????内的两条相交直线a, b
的方向向量分别为u, v.
依题意有 即
?
例题
????
?
设平面????的法向量为n,
?
????
?
a
b
P
已知:如图,
求证: .
分析:进一步可以证明n与平面????内的任意一个向量都垂直,
即n也是????的法向量.
所以 .
?
例题
????
?
????
?
a
b
P
证明:
直线a, b的方向向量分别为u, v.
因为
所以 即 .
又因为 ,
例题
????
?
已知:如图,
求证: .
设平面????的法向量为n,
?
????
?
a
b
P
证明:
使得 .
从而 .
即 . 所以, n也是平面????的法向量.
故 .
?
例题
????
?
????
?
a
b
P
已知:如图,
求证: .
所以对任意点 , 存在 ,
Q
证明:设平面????的法向量为n, 直线a,b的方向向量分别为
u,v.
因为 ,所以 即 .
又因为 ,
?
从有限到所有
所以对任意点 , 存在 , 使得 .
从而 . 即 .
所以,向量n也是平面????的法向量,故 .
?
小结
向量的运算
向量法
例题
分析:
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
是否存在P?
找到P
如何判断
P在哪儿?
P在B1C上
如何表示
如何确定????
?
A1P//面ACD1
向量运算
确定存在
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
x轴、y轴、z轴, 建立如图所示空间直角坐标系Dxyz.
以D为原点, DA, DC, DD1所在直线分别为
证明:
x轴、y轴、z轴, 建立如图所示空间直角坐标系Dxyz.
可得, A(3,0,0), C(0,4,0), D(0,0,2),
所以
以D为原点, DA, DC, DD1所在直线分别为
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
则有 .
所以
所以
设 是平面ACD1的法向量,
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
于是 是平面ACD1
的一个法向量.
又由于A1(3,0,2), C(0,4,0),
B1(3,4,2),
取 z = 6,则x = 4,y = 3,
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
设点P满足
则 .
所以
所以
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
解得 .
所以,当 ,
即P为B1C的中点时,
有 A1P//平面ACD1.
令 , 得
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
小结
用向量法解决立体几何问题的步骤:
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果“翻译”为几何结论.
例题
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量运算的
坐标表示
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
问题5:本节课主要学习了哪些知识内容?
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果”翻译”为几何结论.
数学运算
直观想象
逻辑推理
问题6:请你总结用向量法解决几何问题的步骤.
课堂小结
1. 如图, 在四面体ABCD中, E是BC的中点. 直线AD上是否存在点F, 使得AE//CF?
课后作业
2. 如图, 在正方体ABCD-A1B1C1D1中, E, F分别是面AB1, 面A1C1的中心. 求证:EF//平面ACD1.
课后作业
位置关系(2)
回顾
直线
平面
方向向量
法向量
位置关系
位置关系
立体几何
空间向量
问题1:如何用空间向量表示空间中的直线、平面?
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题2:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
问题3:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
新知
????
?
设 是直线 的方向向量,
是平面????的法向量,
?
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
问题4:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
新知
????
?
????
?
设 分别是平面 的法向量,
证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行, 则这两个平面平行.
例题
????
?
已知:如图,
求证: .
????
?
a
b
P
已知:如图,
求证: .
分析:
平面????内的两条相交直线a, b
的方向向量分别为u, v.
依题意有 即
?
例题
????
?
设平面????的法向量为n,
?
????
?
a
b
P
已知:如图,
求证: .
分析:进一步可以证明n与平面????内的任意一个向量都垂直,
即n也是????的法向量.
所以 .
?
例题
????
?
????
?
a
b
P
证明:
直线a, b的方向向量分别为u, v.
因为
所以 即 .
又因为 ,
例题
????
?
已知:如图,
求证: .
设平面????的法向量为n,
?
????
?
a
b
P
证明:
使得 .
从而 .
即 . 所以, n也是平面????的法向量.
故 .
?
例题
????
?
????
?
a
b
P
已知:如图,
求证: .
所以对任意点 , 存在 ,
Q
证明:设平面????的法向量为n, 直线a,b的方向向量分别为
u,v.
因为 ,所以 即 .
又因为 ,
?
从有限到所有
所以对任意点 , 存在 , 使得 .
从而 . 即 .
所以,向量n也是平面????的法向量,故 .
?
小结
向量的运算
向量法
例题
分析:
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
是否存在P?
找到P
如何判断
P在哪儿?
P在B1C上
如何表示
如何确定????
?
A1P//面ACD1
向量运算
确定存在
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
x轴、y轴、z轴, 建立如图所示空间直角坐标系Dxyz.
以D为原点, DA, DC, DD1所在直线分别为
证明:
x轴、y轴、z轴, 建立如图所示空间直角坐标系Dxyz.
可得, A(3,0,0), C(0,4,0), D(0,0,2),
所以
以D为原点, DA, DC, DD1所在直线分别为
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
则有 .
所以
所以
设 是平面ACD1的法向量,
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
于是 是平面ACD1
的一个法向量.
又由于A1(3,0,2), C(0,4,0),
B1(3,4,2),
取 z = 6,则x = 4,y = 3,
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
设点P满足
则 .
所以
所以
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
证明:
解得 .
所以,当 ,
即P为B1C的中点时,
有 A1P//平面ACD1.
令 , 得
例题
如图, 长方体ABCD-A1B1C1D1中, AB=4, BC=3, CC1=2. 在线段B1C上是否存在点P, 使得A1P//平面ACD1?
小结
用向量法解决立体几何问题的步骤:
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果“翻译”为几何结论.
例题
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量运算的
坐标表示
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
问题5:本节课主要学习了哪些知识内容?
(一)建系;
(二)设点;
(三)表示相关向量;
(四)进行向量运算;
(五)把向量运算的结果”翻译”为几何结论.
数学运算
直观想象
逻辑推理
问题6:请你总结用向量法解决几何问题的步骤.
课堂小结
1. 如图, 在四面体ABCD中, E是BC的中点. 直线AD上是否存在点F, 使得AE//CF?
课后作业
2. 如图, 在正方体ABCD-A1B1C1D1中, E, F分别是面AB1, 面A1C1的中心. 求证:EF//平面ACD1.
课后作业
