高中数学人教A版(2019)选择性必修第一册第一章1.3.1空间直角坐标系-课件(共69张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.3.1空间直角坐标系-课件(共69张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览







文档简介
空间直角坐标系
问题1:类比平面直角坐标系,你能猜想如何构建空间直角坐标系吗?
追问1:平面直角坐标系包含哪些要素?
类比到空间直角坐标系,它包括哪些要素?这些要素需要满足什么条件?
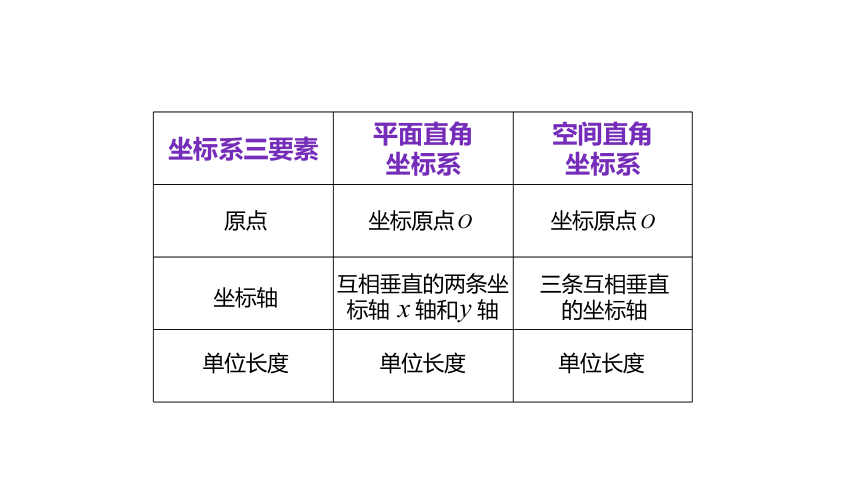
{5940675A-B579-460E-94D1-54222C63F5DA}坐标系三要素
平面直角
坐标系
空间直角
坐标系
坐标原点
单位长度
三条互相垂直的坐标轴
坐标原点
互相垂直的两条坐标轴 轴和 轴
单位长度
原点
坐标轴
单位长度
追问2:你能否给出空间直角坐标系的定义呢?
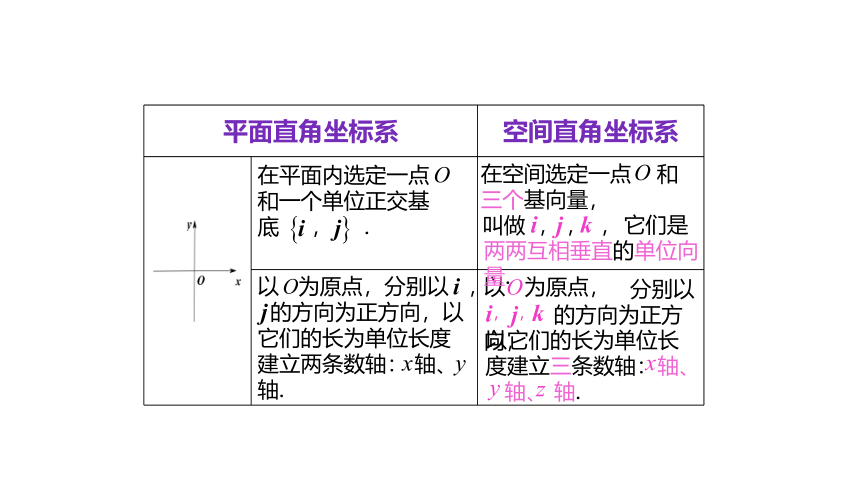
{5940675A-B579-460E-94D1-54222C63F5DA}平面直角坐标系
空间直角坐标系
在平面内选定一点 和一个单位正交基底 , .
以 为原点,分别以 ,
的方向为正方向,以它们的长为单位长度建立两条数轴: 轴、 轴.
叫做 , , ,
在空间选定一点 和三个基向量,
以 为原点,
, ,
它们是两两互相垂直的单位向量.
分别以
的方向为正方向,
以它们的长为单位长度建立三条数轴:轴、
轴、 轴.
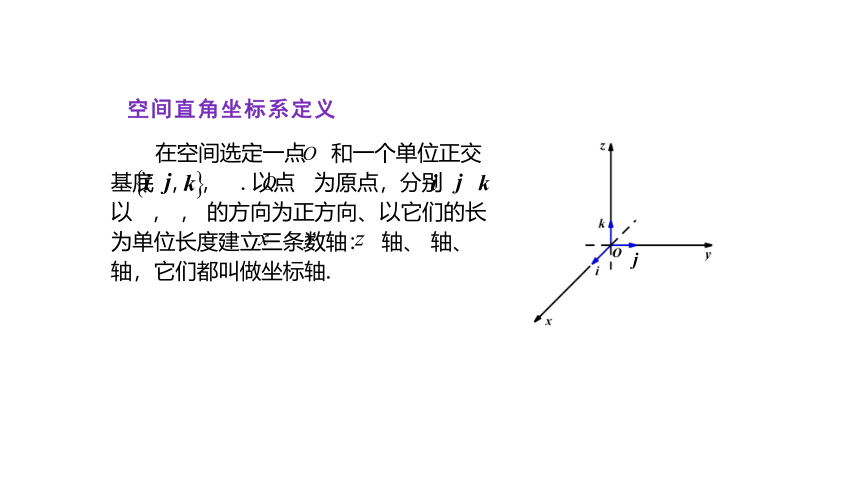
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , .
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , .
空间直角坐标系定义
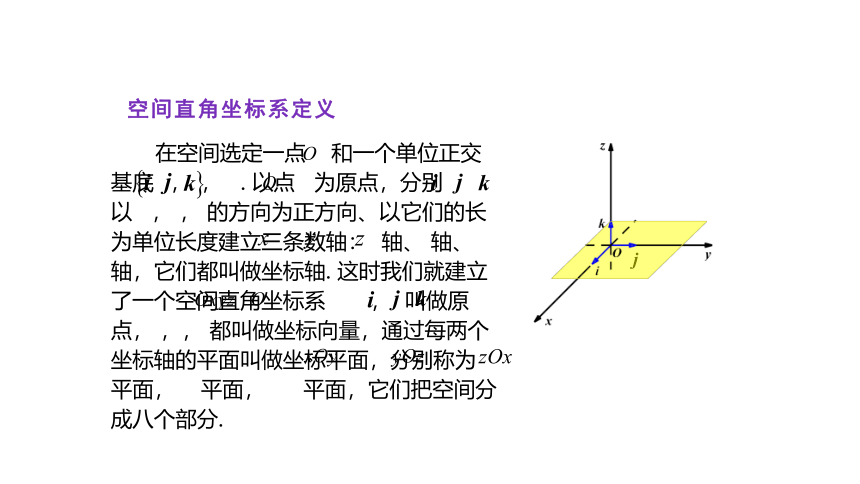
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴.
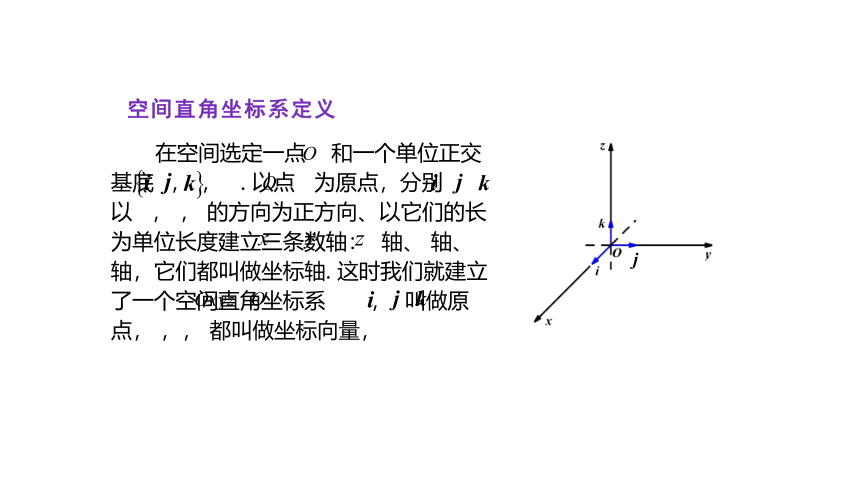
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
追问3:空间直角坐标系如何画呢?
平面直角坐标系
空间直角坐标系
平面直角坐标系
空间直角坐标系
平面直角坐标系
空间直角坐标系
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
问题2:在平面直角坐标系中,每一个点和向量都可以用一对有序实数(即它的坐标)表示,对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问2:在空间直角坐标系中如何定义 的坐标呢?
{5940675A-B579-460E-94D1-54222C63F5DA}平面直角坐标系内
空间直角坐标系内
取与 轴、 轴方向相同的两个单位向量 , 为基底,由平面向量基本定理,有且只有一对实数 , ,使得 . 我们把有序数对 , 叫做 的坐标,记作 , .
取与 轴、 轴、 轴方向相同的单位向量 , , 为基底,由空间向量基本定理,存在唯一的有序实数组 , , ,使得 .
定义:在单位正交基底 ,, 下与向量 对应的有序实数组 , , ,叫做点 在空间直角坐标系中的坐标,记作 , , , 其中 叫做点 的横坐标, 叫做点 的纵坐标, 叫做点 的竖坐标.
追问2:在空间直角坐标系中如何定义 的坐标呢?
追问3:对于给定的向量 又该如何定义它的坐标呢?
追问3:对于给定的向量 又该如何定义它的坐标呢?
我们在空间直角坐标系 中可以作 .
我们在空间直角坐标系 中可以作 .
由空间向量基本定理,存在唯一的有序实数组 , , ,使
有序实数组 ,, 叫做 在空间直角坐标系 中的坐标,上式可简记为 , ,
追问3:对于给定的向量 又该如何定义它的坐标呢?
问题3: 在空间直角坐标系 中,对空间任意一点 ,或任意一个向量 ,你能借助几何直观确定它们的坐标 , , 吗?
过点 分别作垂直于 轴、 轴和 轴的平面
过点 分别作垂直于 轴、 轴和 轴的平面
过点 分别作垂直于 轴、 轴和 轴的平面,
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
即点 或者向量 的坐标就是 , , .
思路小结:目前,我们有哪些方法可以用于确定空间中一个点 或任意一个向量 的坐标呢?
点 的坐标
给定的向量 的坐标
的坐标
?
?
应用空间向量基本定理确定坐标
根据几何直观确定 在各坐标轴上的投影向量,从而求得坐标
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
(2)写出向量 , , , 的坐标.
追问1:题目条件中的 , , 为什么是单位正交基底?
由图可知, 在 轴上,且 ,所以
,
同理 , ,所以 , ,
是单位正交基底.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
追问2:求空间点的坐标我们有哪些
基本解题思路?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问3:观察图形,所求的 , , ,
四点的位置有什么不同?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
解:因为点 在 轴上,且 ,根据
空间向量基本定理易得 .
所以点 的坐标是 , , .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
解:同理,点 的坐标就是 的坐标,由空间向量基本定理易得 . 所以点 的坐标是 , , .
{5940675A-B579-460E-94D1-54222C63F5DA}点的位置
点的坐标
点 在 轴上
方法提炼:
点 在 轴上
, ,
, ,
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
点 在 轴、 轴和 轴上的射影分别是 ,, ,它们在坐标轴上的坐标分别是 ,, ,所以点 的坐标是 ,, .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
点 在 轴、 轴和 轴上的射影分别是 , , ,它们在坐标轴上的坐标分别是 , , ,所以点 的坐标是 ,, .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
思路小结:
1)过点分别作各坐标轴的垂面;
2)确定点在坐标轴上的射影的坐标;
3)得到空间点的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
(2)写出向量 , , , 的坐标.
追问5:怎么求解空间给定向量的坐标?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
追问6:观察几何体,有没有过原点的向
量与所求向量相等?
在长方体中易知 , ,
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
,
.
追问7:对于 和 ,没有棱所在的向
量与它们相等,那又该怎么办呢?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
思路小结:通过分析几何体的结构特征,将所求向量写成基向量的和,从而得到空间向量的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题5:回顾本节课的学习过程,我们是如何得到空间点和
空间向量的坐标表示的?
问题6:如何求空间点或向量的坐标呢?
课后作业
1. 在空间直角坐标系中标出下列各点:
2. 在长方体 中, , , , 与
相交于点 ,建立如图所示的空间直角坐标系 .
(1)写出点 的坐标;
(2)写出向量 , 的坐标.
, , , , , , , , , , ,
谢谢观看
祝同学们学习生活愉快!
问题1:类比平面直角坐标系,你能猜想如何构建空间直角坐标系吗?
追问1:平面直角坐标系包含哪些要素?
类比到空间直角坐标系,它包括哪些要素?这些要素需要满足什么条件?
{5940675A-B579-460E-94D1-54222C63F5DA}坐标系三要素
平面直角
坐标系
空间直角
坐标系
坐标原点
单位长度
三条互相垂直的坐标轴
坐标原点
互相垂直的两条坐标轴 轴和 轴
单位长度
原点
坐标轴
单位长度
追问2:你能否给出空间直角坐标系的定义呢?
{5940675A-B579-460E-94D1-54222C63F5DA}平面直角坐标系
空间直角坐标系
在平面内选定一点 和一个单位正交基底 , .
以 为原点,分别以 ,
的方向为正方向,以它们的长为单位长度建立两条数轴: 轴、 轴.
叫做 , , ,
在空间选定一点 和三个基向量,
以 为原点,
, ,
它们是两两互相垂直的单位向量.
分别以
的方向为正方向,
以它们的长为单位长度建立三条数轴:轴、
轴、 轴.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , .
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , .
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
空间直角坐标系定义
在空间选定一点 和一个单位正交基底 , , . 以点 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系 , 叫做原点, ,, 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成八个部分.
追问3:空间直角坐标系如何画呢?
平面直角坐标系
空间直角坐标系
平面直角坐标系
空间直角坐标系
平面直角坐标系
空间直角坐标系
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
问题2:在平面直角坐标系中,每一个点和向量都可以用一对有序实数(即它的坐标)表示,对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问1:空间中任意一点 与哪个向量的坐标相同?
追问2:在空间直角坐标系中如何定义 的坐标呢?
{5940675A-B579-460E-94D1-54222C63F5DA}平面直角坐标系内
空间直角坐标系内
取与 轴、 轴方向相同的两个单位向量 , 为基底,由平面向量基本定理,有且只有一对实数 , ,使得 . 我们把有序数对 , 叫做 的坐标,记作 , .
取与 轴、 轴、 轴方向相同的单位向量 , , 为基底,由空间向量基本定理,存在唯一的有序实数组 , , ,使得 .
定义:在单位正交基底 ,, 下与向量 对应的有序实数组 , , ,叫做点 在空间直角坐标系中的坐标,记作 , , , 其中 叫做点 的横坐标, 叫做点 的纵坐标, 叫做点 的竖坐标.
追问2:在空间直角坐标系中如何定义 的坐标呢?
追问3:对于给定的向量 又该如何定义它的坐标呢?
追问3:对于给定的向量 又该如何定义它的坐标呢?
我们在空间直角坐标系 中可以作 .
我们在空间直角坐标系 中可以作 .
由空间向量基本定理,存在唯一的有序实数组 , , ,使
有序实数组 ,, 叫做 在空间直角坐标系 中的坐标,上式可简记为 , ,
追问3:对于给定的向量 又该如何定义它的坐标呢?
问题3: 在空间直角坐标系 中,对空间任意一点 ,或任意一个向量 ,你能借助几何直观确定它们的坐标 , , 吗?
过点 分别作垂直于 轴、 轴和 轴的平面
过点 分别作垂直于 轴、 轴和 轴的平面
过点 分别作垂直于 轴、 轴和 轴的平面,
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
过点 分别作垂直于 轴、 轴和 轴的平面,依次交 轴、 轴和 轴于点 , 和 .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
即点 或者向量 的坐标就是 , , .
思路小结:目前,我们有哪些方法可以用于确定空间中一个点 或任意一个向量 的坐标呢?
点 的坐标
给定的向量 的坐标
的坐标
?
?
应用空间向量基本定理确定坐标
根据几何直观确定 在各坐标轴上的投影向量,从而求得坐标
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
(2)写出向量 , , , 的坐标.
追问1:题目条件中的 , , 为什么是单位正交基底?
由图可知, 在 轴上,且 ,所以
,
同理 , ,所以 , ,
是单位正交基底.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
追问2:求空间点的坐标我们有哪些
基本解题思路?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问3:观察图形,所求的 , , ,
四点的位置有什么不同?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
解:因为点 在 轴上,且 ,根据
空间向量基本定理易得 .
所以点 的坐标是 , , .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
解:同理,点 的坐标就是 的坐标,由空间向量基本定理易得 . 所以点 的坐标是 , , .
{5940675A-B579-460E-94D1-54222C63F5DA}点的位置
点的坐标
点 在 轴上
方法提炼:
点 在 轴上
, ,
, ,
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
点 在 轴、 轴和 轴上的射影分别是 ,, ,它们在坐标轴上的坐标分别是 ,, ,所以点 的坐标是 ,, .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
追问4:点 在 轴、 轴、 轴的射影点是谁?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
点 在 轴、 轴和 轴上的射影分别是 , , ,它们在坐标轴上的坐标分别是 , , ,所以点 的坐标是 ,, .
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
思路小结:
1)过点分别作各坐标轴的垂面;
2)确定点在坐标轴上的射影的坐标;
3)得到空间点的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(1)写出 , , , 四点的坐标;
(2)写出向量 , , , 的坐标.
追问5:怎么求解空间给定向量的坐标?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
追问6:观察几何体,有没有过原点的向
量与所求向量相等?
在长方体中易知 , ,
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
,
.
追问7:对于 和 ,没有棱所在的向
量与它们相等,那又该怎么办呢?
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
思路小结:通过分析几何体的结构特征,将所求向量写成基向量的和,从而得到空间向量的坐标.
问题4 如图,在长方体 中, , ,
, 以 , , 为单位正交基底,建立如图
所示的空间直角坐标系 .
(2)写出向量 , , , 的坐标.
问题5:回顾本节课的学习过程,我们是如何得到空间点和
空间向量的坐标表示的?
问题6:如何求空间点或向量的坐标呢?
课后作业
1. 在空间直角坐标系中标出下列各点:
2. 在长方体 中, , , , 与
相交于点 ,建立如图所示的空间直角坐标系 .
(1)写出点 的坐标;
(2)写出向量 , 的坐标.
, , , , , , , , , , ,
谢谢观看
祝同学们学习生活愉快!
