高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究距离、夹角问题(2)-课件(共34张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究距离、夹角问题(2)-课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 21:33:02 | ||
图片预览


文档简介
用空间向量研究距离、夹角问题(2)
空间向量
立体几何
距离问题
夹角问题
角度是对两个方向差的度量
向量是有方向
的量
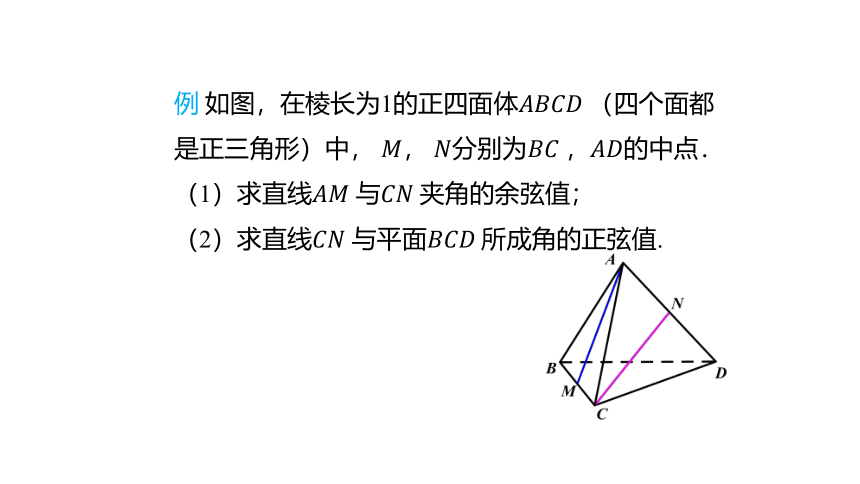
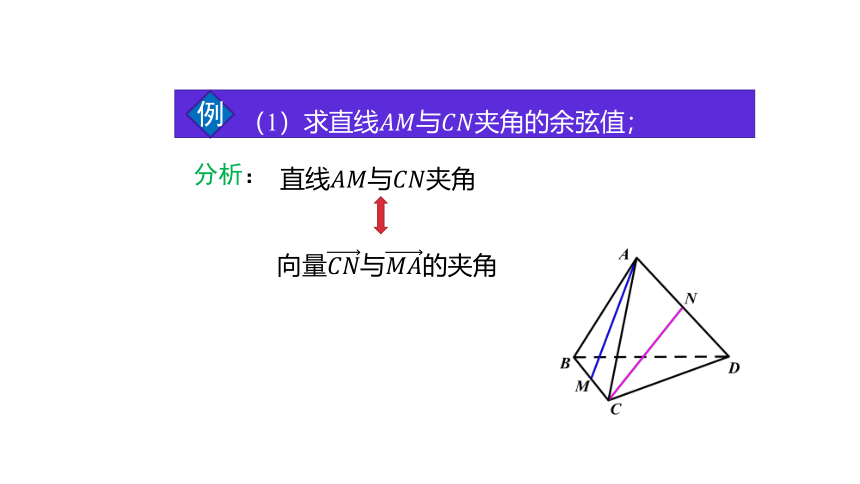
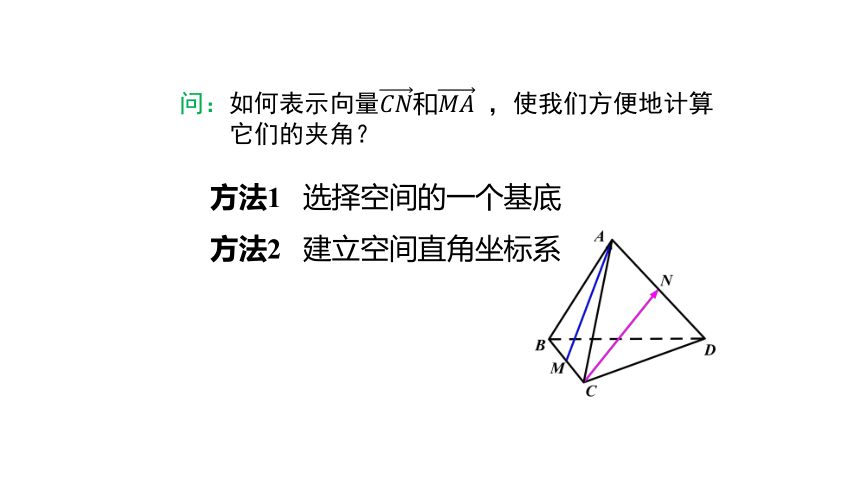
例 如图,在棱长为1的正四面体?????????????????(四个面都是正三角形)中, ????, ????分别为???????? ,????????的中点.
(1)求直线???????? 与?????????夹角的余弦值;
(2)求直线???????? 与平面?????????????所成角的正弦值.
?
直线与平面
所成的角
两条直线
的夹角
本节课的任务:
夹角问题
空间向量
两条直线夹角的定义
两条直线 夹角的取值范围
两条直线夹角的向量求法
问题1 如何用空间向量求两条直线的夹角?
两条直线夹角问题的研究路径:
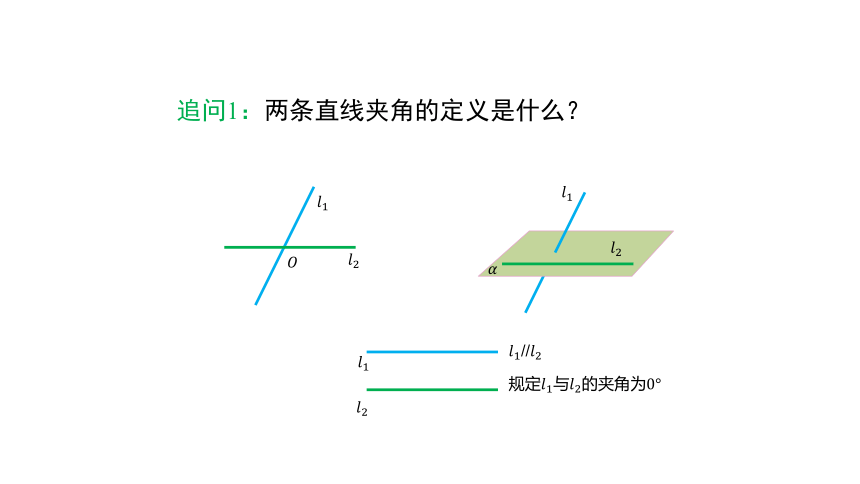
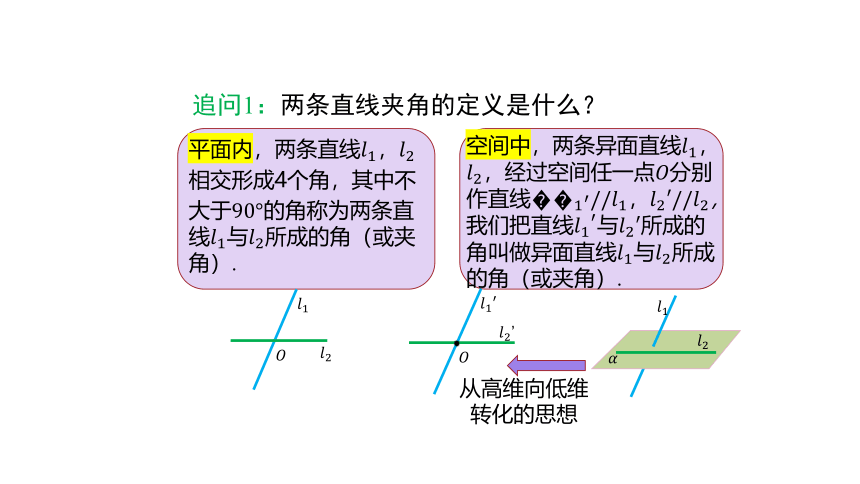
追问1:两条直线夹角的定义是什么?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????2
?
????1
?
????1//????2
?
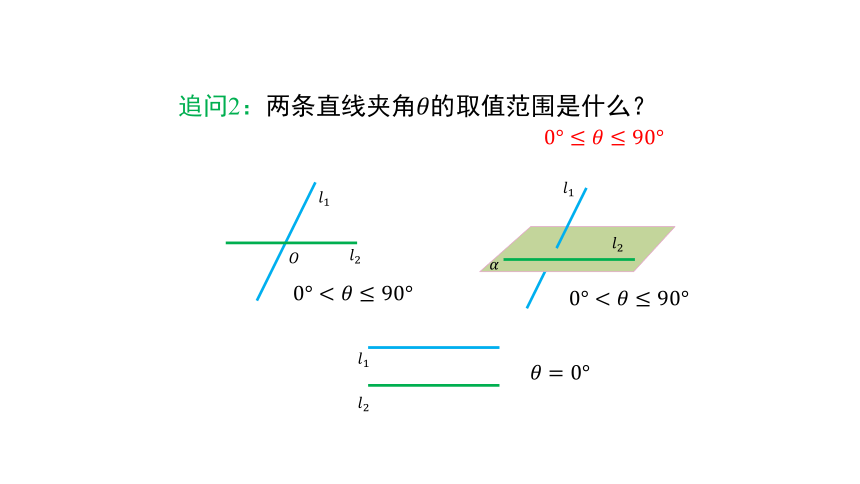
规定????1与????2的夹角为0°
?
平面内,两条直线????1,????2相交形成4个角,其中不大于90°的角称为两条直线????1与????2所成的角(或夹角).
?
空间中,两条异面直线????1,????2,经过空间任一点????分别作直线??1′//????1,????2′//????2,我们把直线????1′与????2′所成的角叫做异面直线????1与????2所成的角(或夹角).
?
追问1:两条直线夹角的定义是什么?
????2
?
????1
?
????
?
????2’
?
????1′
?
????
?
从高维向低维转化的思想
????1
?
????2
?
????
?
追问2:两条直线夹角????的取值范围是什么?
?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????2
?
????1
?
????=0°
?
0°?
0°?
0°≤????≤90°
?
????=??????,?????
?
或????=π??????,????
?
????1
?
????2
?
????
?
追问3:两条直线的夹角????与它们方向向量的夹角有什么关系?
?
cos????=cos????,????
?
直线????1的方向向量为????
?
直线????2的方向向量为????
?
分析:
直线????????与????????夹角
?
向量????????与????????的夹角
?
(1)求直线????????与????????夹角的余弦值;
?
例
方法1 选择空间的一个基底
方法2 建立空间直角坐标系
问:如何表示向量????????和???????? ,使我们方便地计算
它们的夹角?
?
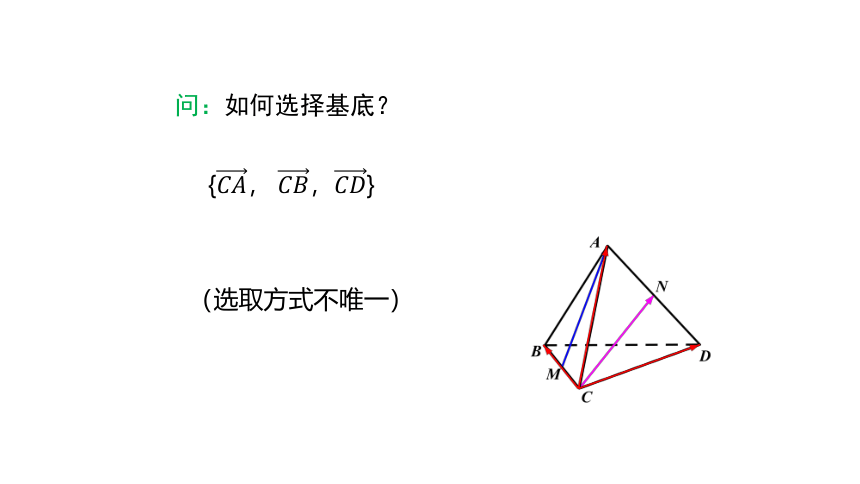
{????????,?????????,????????}?
?
问:如何选择基底?
(选取方式不唯一)
取????????的中点????,过????作????????⊥平面????????????,
?
问:如何建立空间直角坐标系?
取????????的中点????,过????作????????⊥平面????????????,
?
以????为原点,????????,????????,????????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
问:如何建立空间直角坐标系?
(建系方式不唯一)
(1)求直线????????与????????夹角的余弦值;
?
例
解:(1)法1:向量法
以{????????,?????????,????????}?作为基底,则
?
设向量????????与?????????的夹角为????,
则直线????????与????????夹角的余弦值等于cos????.
?
12????????+????????.
?
????????=
?
=?????????12????????,
?
?????????????????
?
????????=
?
?????????????????=12(????????+?????????)?(?????????12????????)
?
=12????????2?14??????????????????+12??????????????????14?????????????????
?
=12?18+14?18=12.
?
又因为△????????????和△????????????均为等边三角形,
?
所以????????=????????
?
=32.
?
所以cos????=?????????????????????????????????
?
=1232×32=23.
?
所以直线????????与????????夹角的余弦值等于
?
23.
?
(1)求直线????????与????????夹角的余弦值;
?
例
解:(1)法2:坐标法
请同学们课后完成!
取????????中点????,过????作????????⊥平面????????????,
?
以????为原点,????????,????????,????????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
用空间向量求两条直线????1,????2夹角????的步骤与方法:
?
例题小结1
化为向量问题
进行向量运算
回到图形问题
①转化为求两直线????1,????2的方向向量????,????的夹角
?
??②计算cos????,????=??????????????????的值
?
③两条直线????1,????2夹角????的余弦值
?????????????cos????=cos????,????
?
向量法
或坐标法
两条直线夹角的定义
两条直线夹角的取值范围
两条直线夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的向量求法
问题2 如何用空间向量求直线与平面所成的角?
直线与平面所成角问题的研究路径:
直线????与平面????所成的角????:
?
?????????
?
?????//????
?
????⊥????
?
?????=0°
?
?????=0°
?
?????=90°
?
????是????的斜线
?
?????=?
?
????
?
l
????
?
l
????
?
l
????
?
l
A
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
过斜线????上斜足????外一点 ????向平面????引垂线???????? ,过垂足???? 和斜足????的直线???????? 叫做斜线????在平面????上的射影.
?
追问1:斜线与平面所成的角的定义是什么?
????
?
l
B
C
追问2:直线与平面所成角????的取值范围是什么?
?
?????????
?
?????//????
?
????⊥????
?
?????=0°
?
?????=0°
?
?????=90°
?
????是????的斜线
?
?0°?
????
?
l
????
?
l
????
?
????
?
l
0°≤????≤90°
?
????+????,????=π2
?
追问3:直线与平面所成的角????和????,????有什么关系?
?
或????+π2=????,????
?
A
????
?
l
B
C
sin????=cos????,????
?
直线????的方向向量为????
?
平面????的法向量为????
?
(2)求直线????????与平面????????????所成角的正弦值.
?
例
直线????????与平面????????????所成的角
?
向量????????与平面????????????的法向量????的夹角
?
分析:
问:如何表示平面????????????法向量?
?
方法1 选择空间的一个基底
方法2 建立空间直角坐标系
????????=
?
请给出相应点和向量的坐标.
????(36,0,63),
?
????(312,14,66),
?
(?5312,14,66),
?
????(32,0,0),
?
????(0,12,0),
?
n=0,0,1.
?
(2)求直线????????与平面????????????所成角的正弦值.
?
例
解:(2)
????????=?5312,14,66,
?
n=(0,0,1)为平面????????????的法向量.
?
设直线????????与平面????????????所成的角????,则sin????=cos????????,?????.
?
因为cos????????,?????=???????????????????????????
?
所以直线????????与平面????????????所成的角正弦值等于
?
23.
?
=6632×1=23,
?
用空间向量求直线?????与平面????所成角????的步骤和方法:
?
化为向量问题
进行向量运算
回到图形问题
①转化为求直线????的方向向量????与平面????的法向量????的夹角
?
??②计算cos????,????=??????????????????的值
?
③直线????与平面????所成的角????的 正弦值??sin????=cos????,????
?
例题小结2
1.学会两类夹角问题的向量求法
问题3 回顾本节课的探究过程,你学习到了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的类型
角的取值范围
方向向量与法向量
与向量夹角的关系
两条直线的夹角的定义
两条直线的夹角的取值范围
两条直线的夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的
向量求法
2. 体验研究夹角问题的方法和过程
问题3 回顾本节课的探究过程,你学习到了什么?
3.体会应用空间向量求夹角问题的“三步曲”
问题3 回顾本节课的探究过程,你学习到了什么?
cos????=cos????,????
?
sin????=cos????,????
?
向量化
向量运算
几何化
向量夹角问题
向量夹角
结论
线线角、线面角问题
线线角、线面角结论
向量——解决度量问题的有力工具!
课后作业
1. 在直三棱柱?????????????????1????1????1中,∠????????????=90°,????1,????1分别是????1????1,????1????1的中点,????????=????????=????????1,则????????1与????????1所成角的余弦值是( )
(A)3010 (B)?12 (C) 3015 (D)?1510
?
课后作业
2. 长方体?????????????????????1????1????1????1中,????????=????????1=2,????????=4,????,????分别是????1????1,????????的中点,????是????????1与??1????的交点.求直线????????与平面????????????所成角的正弦值.
空间向量
立体几何
距离问题
夹角问题
角度是对两个方向差的度量
向量是有方向
的量
例 如图,在棱长为1的正四面体?????????????????(四个面都是正三角形)中, ????, ????分别为???????? ,????????的中点.
(1)求直线???????? 与?????????夹角的余弦值;
(2)求直线???????? 与平面?????????????所成角的正弦值.
?
直线与平面
所成的角
两条直线
的夹角
本节课的任务:
夹角问题
空间向量
两条直线夹角的定义
两条直线 夹角的取值范围
两条直线夹角的向量求法
问题1 如何用空间向量求两条直线的夹角?
两条直线夹角问题的研究路径:
追问1:两条直线夹角的定义是什么?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????2
?
????1
?
????1//????2
?
规定????1与????2的夹角为0°
?
平面内,两条直线????1,????2相交形成4个角,其中不大于90°的角称为两条直线????1与????2所成的角(或夹角).
?
空间中,两条异面直线????1,????2,经过空间任一点????分别作直线??1′//????1,????2′//????2,我们把直线????1′与????2′所成的角叫做异面直线????1与????2所成的角(或夹角).
?
追问1:两条直线夹角的定义是什么?
????2
?
????1
?
????
?
????2’
?
????1′
?
????
?
从高维向低维转化的思想
????1
?
????2
?
????
?
追问2:两条直线夹角????的取值范围是什么?
?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????2
?
????1
?
????=0°
?
0°?
0°?
0°≤????≤90°
?
????=??????,?????
?
或????=π??????,????
?
????1
?
????2
?
????
?
追问3:两条直线的夹角????与它们方向向量的夹角有什么关系?
?
cos????=cos????,????
?
直线????1的方向向量为????
?
直线????2的方向向量为????
?
分析:
直线????????与????????夹角
?
向量????????与????????的夹角
?
(1)求直线????????与????????夹角的余弦值;
?
例
方法1 选择空间的一个基底
方法2 建立空间直角坐标系
问:如何表示向量????????和???????? ,使我们方便地计算
它们的夹角?
?
{????????,?????????,????????}?
?
问:如何选择基底?
(选取方式不唯一)
取????????的中点????,过????作????????⊥平面????????????,
?
问:如何建立空间直角坐标系?
取????????的中点????,过????作????????⊥平面????????????,
?
以????为原点,????????,????????,????????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
问:如何建立空间直角坐标系?
(建系方式不唯一)
(1)求直线????????与????????夹角的余弦值;
?
例
解:(1)法1:向量法
以{????????,?????????,????????}?作为基底,则
?
设向量????????与?????????的夹角为????,
则直线????????与????????夹角的余弦值等于cos????.
?
12????????+????????.
?
????????=
?
=?????????12????????,
?
?????????????????
?
????????=
?
?????????????????=12(????????+?????????)?(?????????12????????)
?
=12????????2?14??????????????????+12??????????????????14?????????????????
?
=12?18+14?18=12.
?
又因为△????????????和△????????????均为等边三角形,
?
所以????????=????????
?
=32.
?
所以cos????=?????????????????????????????????
?
=1232×32=23.
?
所以直线????????与????????夹角的余弦值等于
?
23.
?
(1)求直线????????与????????夹角的余弦值;
?
例
解:(1)法2:坐标法
请同学们课后完成!
取????????中点????,过????作????????⊥平面????????????,
?
以????为原点,????????,????????,????????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
用空间向量求两条直线????1,????2夹角????的步骤与方法:
?
例题小结1
化为向量问题
进行向量运算
回到图形问题
①转化为求两直线????1,????2的方向向量????,????的夹角
?
??②计算cos????,????=??????????????????的值
?
③两条直线????1,????2夹角????的余弦值
?????????????cos????=cos????,????
?
向量法
或坐标法
两条直线夹角的定义
两条直线夹角的取值范围
两条直线夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的向量求法
问题2 如何用空间向量求直线与平面所成的角?
直线与平面所成角问题的研究路径:
直线????与平面????所成的角????:
?
?????????
?
?????//????
?
????⊥????
?
?????=0°
?
?????=0°
?
?????=90°
?
????是????的斜线
?
?????=?
?
????
?
l
????
?
l
????
?
l
????
?
l
A
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
过斜线????上斜足????外一点 ????向平面????引垂线???????? ,过垂足???? 和斜足????的直线???????? 叫做斜线????在平面????上的射影.
?
追问1:斜线与平面所成的角的定义是什么?
????
?
l
B
C
追问2:直线与平面所成角????的取值范围是什么?
?
?????????
?
?????//????
?
????⊥????
?
?????=0°
?
?????=0°
?
?????=90°
?
????是????的斜线
?
?0°?
????
?
l
????
?
l
????
?
????
?
l
0°≤????≤90°
?
????+????,????=π2
?
追问3:直线与平面所成的角????和????,????有什么关系?
?
或????+π2=????,????
?
A
????
?
l
B
C
sin????=cos????,????
?
直线????的方向向量为????
?
平面????的法向量为????
?
(2)求直线????????与平面????????????所成角的正弦值.
?
例
直线????????与平面????????????所成的角
?
向量????????与平面????????????的法向量????的夹角
?
分析:
问:如何表示平面????????????法向量?
?
方法1 选择空间的一个基底
方法2 建立空间直角坐标系
????????=
?
请给出相应点和向量的坐标.
????(36,0,63),
?
????(312,14,66),
?
(?5312,14,66),
?
????(32,0,0),
?
????(0,12,0),
?
n=0,0,1.
?
(2)求直线????????与平面????????????所成角的正弦值.
?
例
解:(2)
????????=?5312,14,66,
?
n=(0,0,1)为平面????????????的法向量.
?
设直线????????与平面????????????所成的角????,则sin????=cos????????,?????.
?
因为cos????????,?????=???????????????????????????
?
所以直线????????与平面????????????所成的角正弦值等于
?
23.
?
=6632×1=23,
?
用空间向量求直线?????与平面????所成角????的步骤和方法:
?
化为向量问题
进行向量运算
回到图形问题
①转化为求直线????的方向向量????与平面????的法向量????的夹角
?
??②计算cos????,????=??????????????????的值
?
③直线????与平面????所成的角????的 正弦值??sin????=cos????,????
?
例题小结2
1.学会两类夹角问题的向量求法
问题3 回顾本节课的探究过程,你学习到了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的类型
角的取值范围
方向向量与法向量
与向量夹角的关系
两条直线的夹角的定义
两条直线的夹角的取值范围
两条直线的夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的
向量求法
2. 体验研究夹角问题的方法和过程
问题3 回顾本节课的探究过程,你学习到了什么?
3.体会应用空间向量求夹角问题的“三步曲”
问题3 回顾本节课的探究过程,你学习到了什么?
cos????=cos????,????
?
sin????=cos????,????
?
向量化
向量运算
几何化
向量夹角问题
向量夹角
结论
线线角、线面角问题
线线角、线面角结论
向量——解决度量问题的有力工具!
课后作业
1. 在直三棱柱?????????????????1????1????1中,∠????????????=90°,????1,????1分别是????1????1,????1????1的中点,????????=????????=????????1,则????????1与????????1所成角的余弦值是( )
(A)3010 (B)?12 (C) 3015 (D)?1510
?
课后作业
2. 长方体?????????????????????1????1????1????1中,????????=????????1=2,????????=4,????,????分别是????1????1,????????的中点,????是????????1与??1????的交点.求直线????????与平面????????????所成角的正弦值.
