高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究距离、夹角问题(3)-课件(共29张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究距离、夹角问题(3)-课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览



文档简介
用空间向量研究距离、夹角问题(3)
α
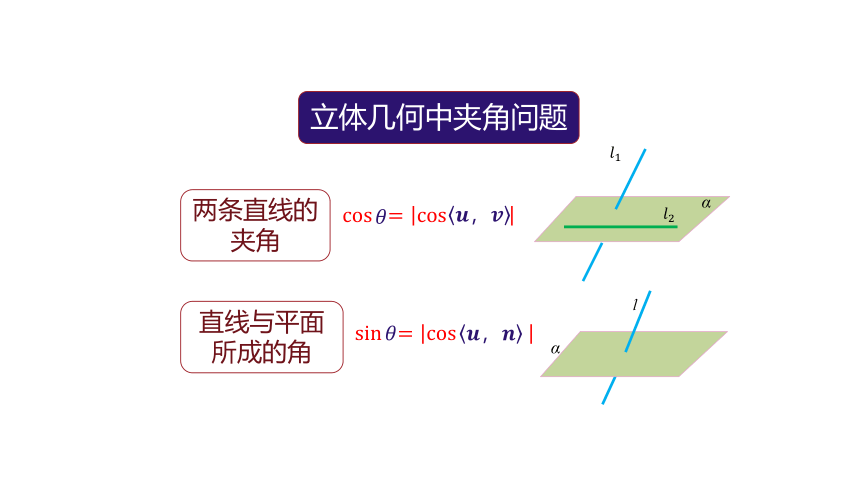
两条直线的夹角
直线与平面所成的角
α
l
????1
?
????2
?
立体几何中夹角问题
cos??=cos?????????????
?
?????????????????????,????
?
????,????
?
????
?
sin??=cos???????????????
?
α
两条直线的夹角
直线与平面所成的角
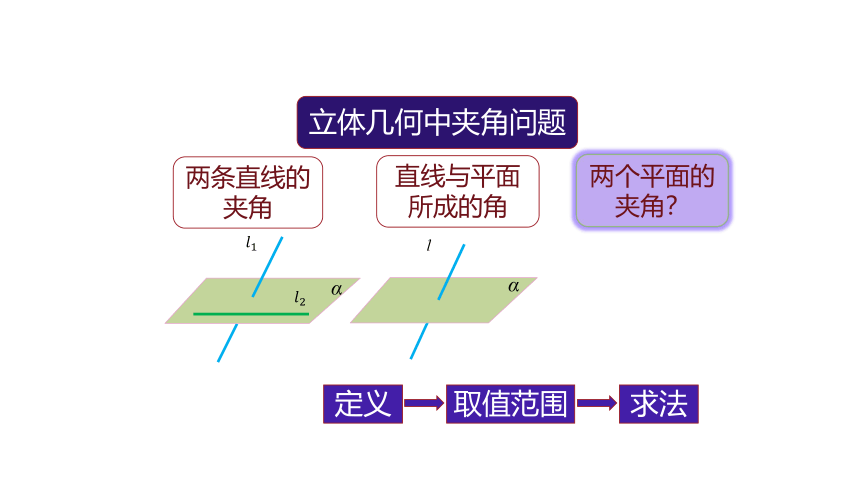
两个平面的夹角?
α
l
定义
取值范围
求法
立体几何中夹角问题
????1
?
????2
?
问题1 类比两条直线夹角的定义,如何定义两个平面的夹角?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
两条直线的夹角
两个平面的夹角
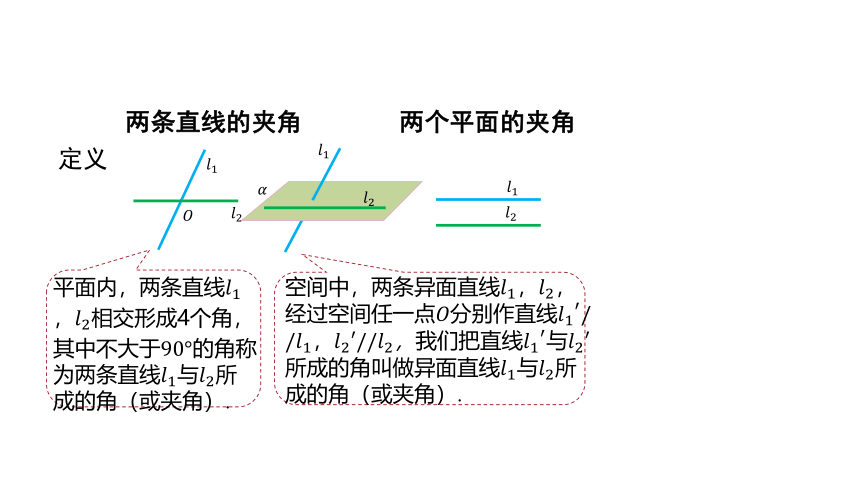
定义
平面内,两条直线????1,????2相交形成4个角,其中不大于90°的角称为两条直线????1与????2所成的角(或夹角).
?
空间中,两条异面直线????1,????2,经过空间任一点????分别作直线????1′//????1,????2′//????2,我们把直线????1′与????2′所成的角叫做异面直线????1与????2所成的角(或夹角).
?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????1
?
????2
?
空间中,平面????与平面????相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面????与平面????的夹角.
?
α
β
α
β
l
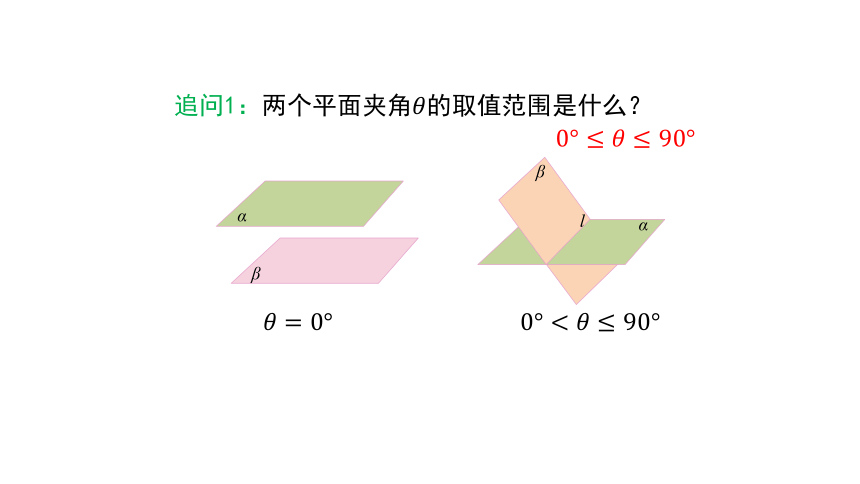
追问1:两个平面夹角????的取值范围是什么?
?
α
β
α
β
l
????=0°
?
0°?
0°≤????≤90°
?
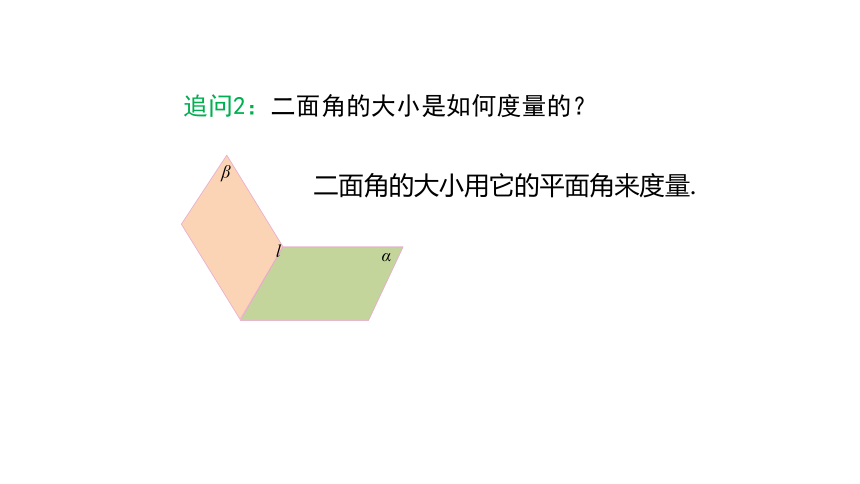
二面角的大小用它的平面角来度量.
α
β
l
追问2:二面角的大小是如何度量的?
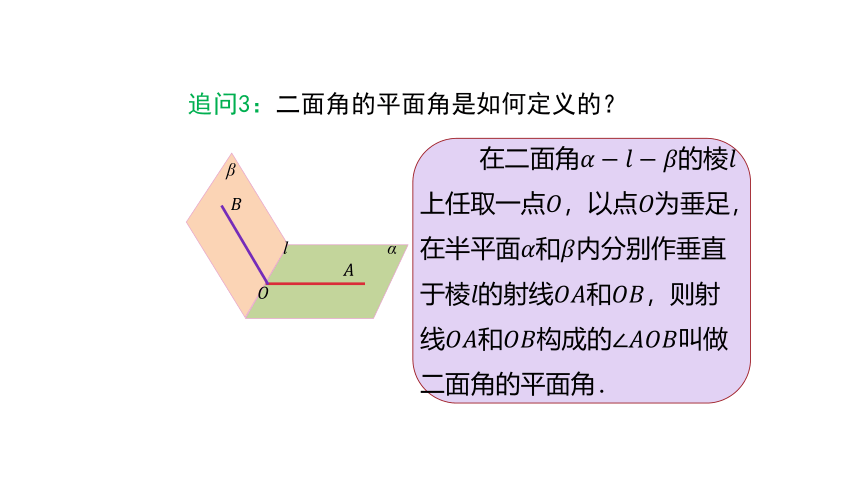
在二面角??????????????的棱????上任取一点????,以点????为垂足,在半平面????和????内分别作垂直于棱????的射线????????和????????,则射线????????和????????构成的∠????????????叫做二面角的平面角.
?
α
β
l
????
?
????
?
????
?
追问3:二面角的平面角是如何定义的?
两个平面的夹角等于相应二面角或其补角
追问4:两个平面夹角的大小与这两个平面形成的二面角的大小有何关系?
α
β
l
????
?
????
?
????
?
问题2 类比两条直线夹角的求法,如何用向量方法求两个平面的夹角?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
两条直线的夹角
两个平面的夹角
定义
范围
向量
求法
将直线的方向向量表示,转化为求向量的夹角
????1
?
????2
?
????
?
????2
?
????1
?
????
?
?
α
β
l
????
?
????
?
????
?
求方向向量????,?????的夹角
?
求得向量????,?????的夹角
?
求直线????,?????的夹角
?
求平面????,?????的夹角
?
转化为“新” 几何问题
转化向量问题
转化为几何结论
求得平面????,?????的夹角
?
向量运算
追问1:如何转化为向量问题?
思路1
转化为求两平面内与交线垂直的直线的方向向量的夹角
未必容易!
α
β
l
????
?
????
?
????
?
????=????????,????????
?
追问2:两个平面的夹角????与这两个平面的法向量的夹角有什么关系?
?
或????=π?????????,????????
?
cos????=cos????????,????????
?
平面????的法向量为????????
?
平面????的法向量为????????
?
α
β
l
????
?
????
?
????
?
求法向量????????,????????的夹角
?
求平面????,?????的夹角
?
转化向量问题
转化为几何结论
求出平面????,?????的夹角
?
向量运算
求出向量????????,????????的夹角
?
转化为向量问题
思路2
????????
?
????????
?
转化求两个平面的
法向量的夹角
建系可求!
α
β
l
????
?
????
?
????
?
如图,在直三棱柱?????????????????1????1????1中,????????=????????=2,????????1=3,∠????????????=90°,????为????????的中点,
?
例
点????,????分别在棱????????1,????????1上,????1????=2????????,????????=2????????1 .
求平面????????????与平面????1????1????1夹角的
余弦值.
?
问:求两个平面的夹角转化为哪种向量的夹角?
2.两个平面的
法向量的夹角
1.两平面内与交线垂直的直线的方向向量的夹角
思路
解:以????1为原点,????1????1,????1????1,????1????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
设平面????1????1????1的法向量为????1,平面????????????的法向量为????2,
则平面????????????与平面????1????1????1的夹角就是????1与????2的夹角或其补角.
?
求平面????????????与平面????1????1????1夹角的余弦值;
?
例
因为????1????⊥平面????1????1????1,
?
因为????(0,1,3),????(2,0,2),
????(0,2,1)?,
?
所以平面????1????1????1的一个法向量为????1=(0,0,1)?.
?
设平面????????????的法向量为????2=????,????,????,
?
又 ????2?????????=0,????2?????????=0,?
?
所以2??????????????=0,?????2????=0?.??????????
?
所以????????=(2,?1,?1),
????????=(0,1,?2) .
?
所以 ????=32????,????=2????.?????取 ????2=?(3,4,2),
?
=22929.
?
则cos????1,????2=????1?????2|????1|?|????2|
?
=0,0,1?3,4,21×29
?
设平面????????????与平面????1????1????1的夹角为????,
?
即平面????????????与平面????1????1????1夹角
的余弦值为
?
则cos????=cos????1,????2
?
=22929.
?
22929.
?
思考:在例题条件下,如何求“平面????1????1????与平面????1????1????1夹角的余弦值”?
?
问:转化为哪种向量的夹角?
2.两个平面的
法向量的夹角
1.两平面内与交线垂直的直线的方向向量的夹角
思路
一般性!
普适性!
用空间向量求平面????与平面????的夹角????的步骤与方法:
?
例题小结
化为向量问题
进行向量运算
回到图形问题
①转化为求平面????,????的法向量????????,????????的夹角
?
??②计算cos????????,????????=??????????????????????????????????的值
?
③平面????与平面????夹角????的余弦值?????????????cos????=cos????????,????????
?
问题3 本节课主要学习了哪些内容?
两个平面夹角的定义
两个平面夹角的向量求法
类比两条直线夹角的研究方法、研究内容、解决方法研究两个平面的夹角
问题4 研究这些内容主要用了什么方法?
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
两条直线的夹角
两个平面的夹角
定义
范围
向量
求法
问题5 用向量方法解决立体几何中夹角问题的一般步骤是什么?
cos????=cos????,????
?
cos????=cos????????,????????
?
sin????=cos????,????
?
向量化
向量运算
几何化
向量夹角问题
向量夹角
结论
线线角、线面角、面面角问题
线线角、线面、面面角结论
1.如图,正三棱柱?????????????????1????1????1中的所有棱长都为2,求平面????1????????1与平面????????1????夹角的余弦值.
?
课后作业
课后作业
2. 如图,△????????????和△????????????所在平面垂直,且????????=????????=????????,∠????????????=∠????????????=120°,求:
?
(1)直线????????与直线????????所成角的大小;
(2)直线????????与平面????????????所成角的大小;
(3)平面????????????和平面????????????的夹角的余弦值.
α
两条直线的夹角
直线与平面所成的角
α
l
????1
?
????2
?
立体几何中夹角问题
cos??=cos?????????????
?
?????????????????????,????
?
????,????
?
????
?
sin??=cos???????????????
?
α
两条直线的夹角
直线与平面所成的角
两个平面的夹角?
α
l
定义
取值范围
求法
立体几何中夹角问题
????1
?
????2
?
问题1 类比两条直线夹角的定义,如何定义两个平面的夹角?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
两条直线的夹角
两个平面的夹角
定义
平面内,两条直线????1,????2相交形成4个角,其中不大于90°的角称为两条直线????1与????2所成的角(或夹角).
?
空间中,两条异面直线????1,????2,经过空间任一点????分别作直线????1′//????1,????2′//????2,我们把直线????1′与????2′所成的角叫做异面直线????1与????2所成的角(或夹角).
?
????1
?
????2
?
????
?
????2
?
????1
?
????
?
????1
?
????2
?
空间中,平面????与平面????相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面????与平面????的夹角.
?
α
β
α
β
l
追问1:两个平面夹角????的取值范围是什么?
?
α
β
α
β
l
????=0°
?
0°?
0°≤????≤90°
?
二面角的大小用它的平面角来度量.
α
β
l
追问2:二面角的大小是如何度量的?
在二面角??????????????的棱????上任取一点????,以点????为垂足,在半平面????和????内分别作垂直于棱????的射线????????和????????,则射线????????和????????构成的∠????????????叫做二面角的平面角.
?
α
β
l
????
?
????
?
????
?
追问3:二面角的平面角是如何定义的?
两个平面的夹角等于相应二面角或其补角
追问4:两个平面夹角的大小与这两个平面形成的二面角的大小有何关系?
α
β
l
????
?
????
?
????
?
问题2 类比两条直线夹角的求法,如何用向量方法求两个平面的夹角?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
两条直线的夹角
两个平面的夹角
定义
范围
向量
求法
将直线的方向向量表示,转化为求向量的夹角
????1
?
????2
?
????
?
????2
?
????1
?
????
?
?
α
β
l
????
?
????
?
????
?
求方向向量????,?????的夹角
?
求得向量????,?????的夹角
?
求直线????,?????的夹角
?
求平面????,?????的夹角
?
转化为“新” 几何问题
转化向量问题
转化为几何结论
求得平面????,?????的夹角
?
向量运算
追问1:如何转化为向量问题?
思路1
转化为求两平面内与交线垂直的直线的方向向量的夹角
未必容易!
α
β
l
????
?
????
?
????
?
????=????????,????????
?
追问2:两个平面的夹角????与这两个平面的法向量的夹角有什么关系?
?
或????=π?????????,????????
?
cos????=cos????????,????????
?
平面????的法向量为????????
?
平面????的法向量为????????
?
α
β
l
????
?
????
?
????
?
求法向量????????,????????的夹角
?
求平面????,?????的夹角
?
转化向量问题
转化为几何结论
求出平面????,?????的夹角
?
向量运算
求出向量????????,????????的夹角
?
转化为向量问题
思路2
????????
?
????????
?
转化求两个平面的
法向量的夹角
建系可求!
α
β
l
????
?
????
?
????
?
如图,在直三棱柱?????????????????1????1????1中,????????=????????=2,????????1=3,∠????????????=90°,????为????????的中点,
?
例
点????,????分别在棱????????1,????????1上,????1????=2????????,????????=2????????1 .
求平面????????????与平面????1????1????1夹角的
余弦值.
?
问:求两个平面的夹角转化为哪种向量的夹角?
2.两个平面的
法向量的夹角
1.两平面内与交线垂直的直线的方向向量的夹角
思路
解:以????1为原点,????1????1,????1????1,????1????所在直线为????轴、????轴、????轴,建立如图所示的空间直角坐标系.
?
设平面????1????1????1的法向量为????1,平面????????????的法向量为????2,
则平面????????????与平面????1????1????1的夹角就是????1与????2的夹角或其补角.
?
求平面????????????与平面????1????1????1夹角的余弦值;
?
例
因为????1????⊥平面????1????1????1,
?
因为????(0,1,3),????(2,0,2),
????(0,2,1)?,
?
所以平面????1????1????1的一个法向量为????1=(0,0,1)?.
?
设平面????????????的法向量为????2=????,????,????,
?
又 ????2?????????=0,????2?????????=0,?
?
所以2??????????????=0,?????2????=0?.??????????
?
所以????????=(2,?1,?1),
????????=(0,1,?2) .
?
所以 ????=32????,????=2????.?????取 ????2=?(3,4,2),
?
=22929.
?
则cos????1,????2=????1?????2|????1|?|????2|
?
=0,0,1?3,4,21×29
?
设平面????????????与平面????1????1????1的夹角为????,
?
即平面????????????与平面????1????1????1夹角
的余弦值为
?
则cos????=cos????1,????2
?
=22929.
?
22929.
?
思考:在例题条件下,如何求“平面????1????1????与平面????1????1????1夹角的余弦值”?
?
问:转化为哪种向量的夹角?
2.两个平面的
法向量的夹角
1.两平面内与交线垂直的直线的方向向量的夹角
思路
一般性!
普适性!
用空间向量求平面????与平面????的夹角????的步骤与方法:
?
例题小结
化为向量问题
进行向量运算
回到图形问题
①转化为求平面????,????的法向量????????,????????的夹角
?
??②计算cos????????,????????=??????????????????????????????????的值
?
③平面????与平面????夹角????的余弦值?????????????cos????=cos????????,????????
?
问题3 本节课主要学习了哪些内容?
两个平面夹角的定义
两个平面夹角的向量求法
类比两条直线夹角的研究方法、研究内容、解决方法研究两个平面的夹角
问题4 研究这些内容主要用了什么方法?
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
两条直线的夹角
两个平面的夹角
定义
范围
向量
求法
问题5 用向量方法解决立体几何中夹角问题的一般步骤是什么?
cos????=cos????,????
?
cos????=cos????????,????????
?
sin????=cos????,????
?
向量化
向量运算
几何化
向量夹角问题
向量夹角
结论
线线角、线面角、面面角问题
线线角、线面、面面角结论
1.如图,正三棱柱?????????????????1????1????1中的所有棱长都为2,求平面????1????????1与平面????????1????夹角的余弦值.
?
课后作业
课后作业
2. 如图,△????????????和△????????????所在平面垂直,且????????=????????=????????,∠????????????=∠????????????=120°,求:
?
(1)直线????????与直线????????所成角的大小;
(2)直线????????与平面????????????所成角的大小;
(3)平面????????????和平面????????????的夹角的余弦值.
