高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究直线、平面的的位置关系(3)-课件(共20张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.4.2用空间向量研究直线、平面的的位置关系(3)-课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 993.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 21:37:29 | ||
图片预览


文档简介
用空间向量研究直线、平面的
位置关系(3)
回顾
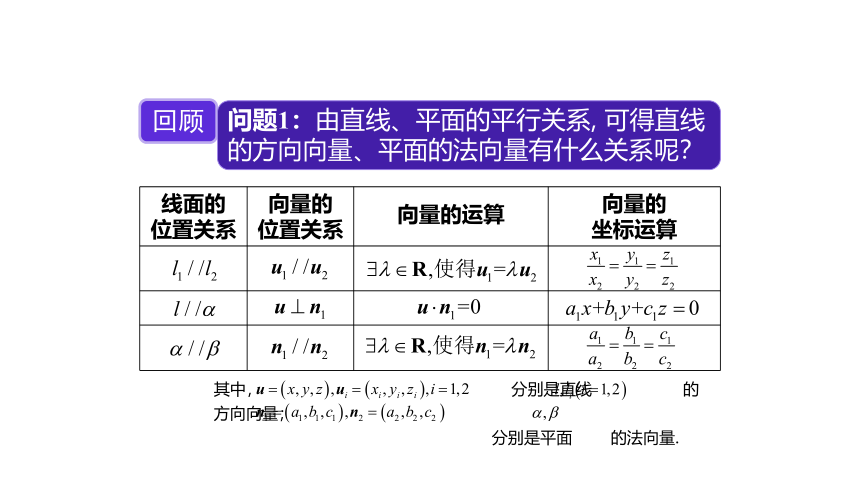
问题1:由直线、平面的平行关系, 可得直线的方向向量、平面的法向量有什么关系呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
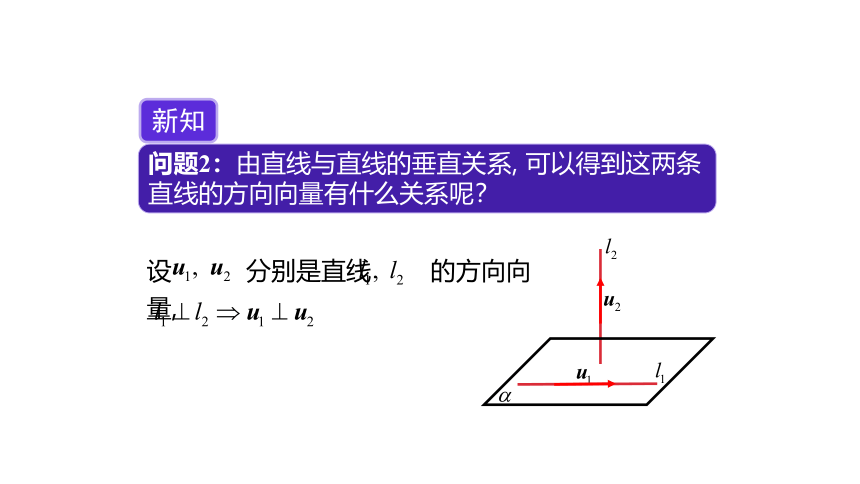
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
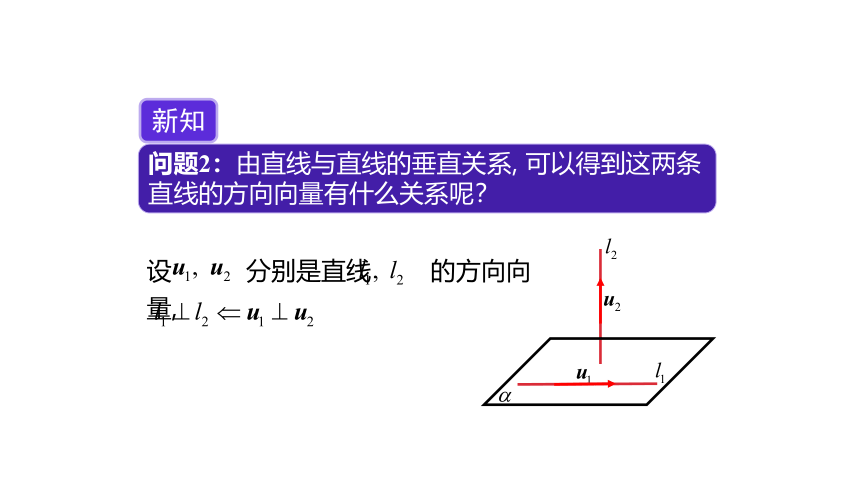
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
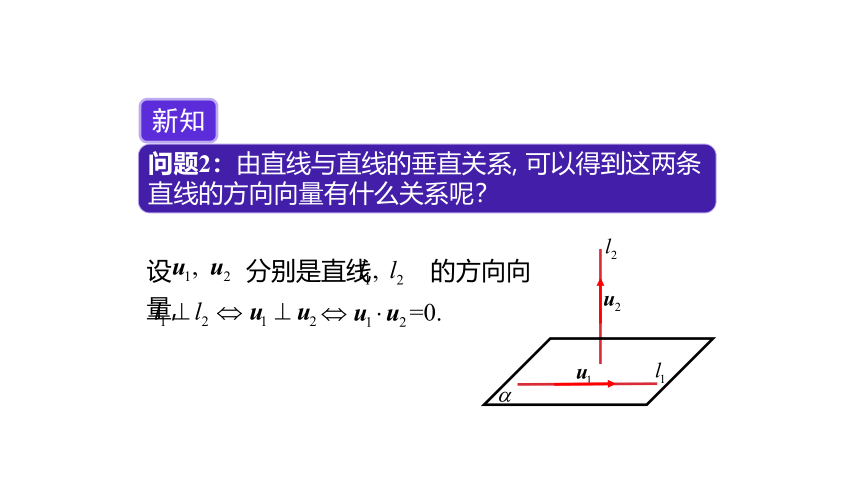
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
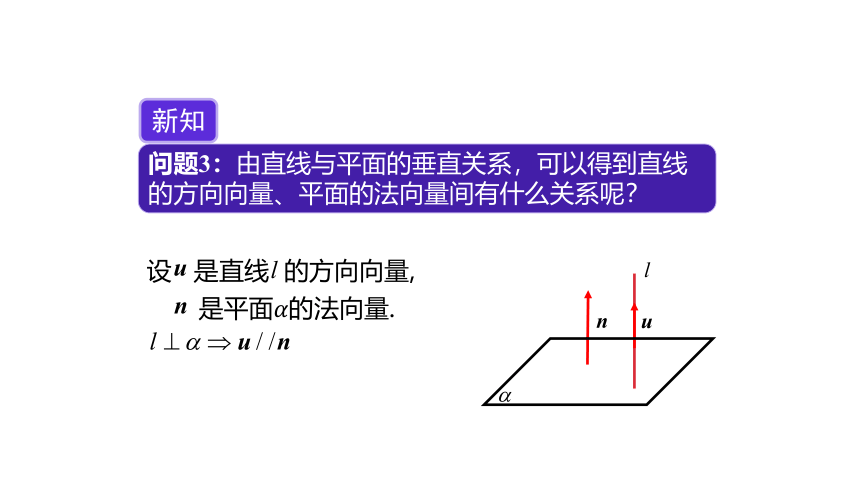
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
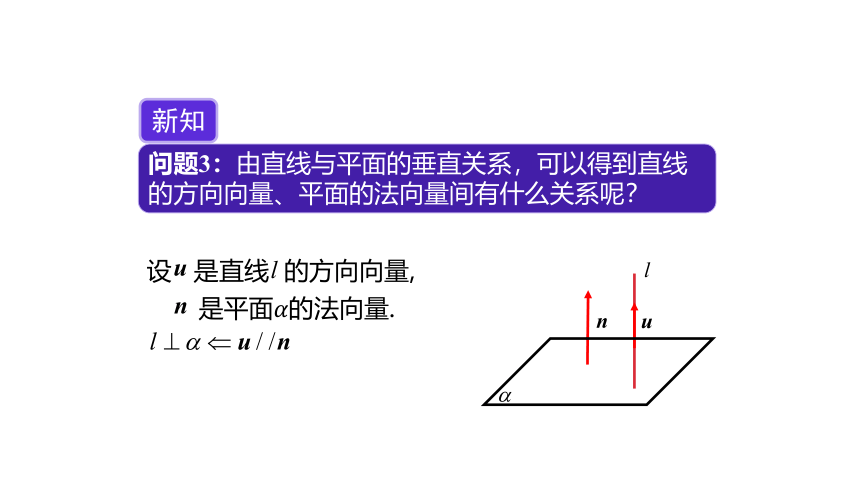
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
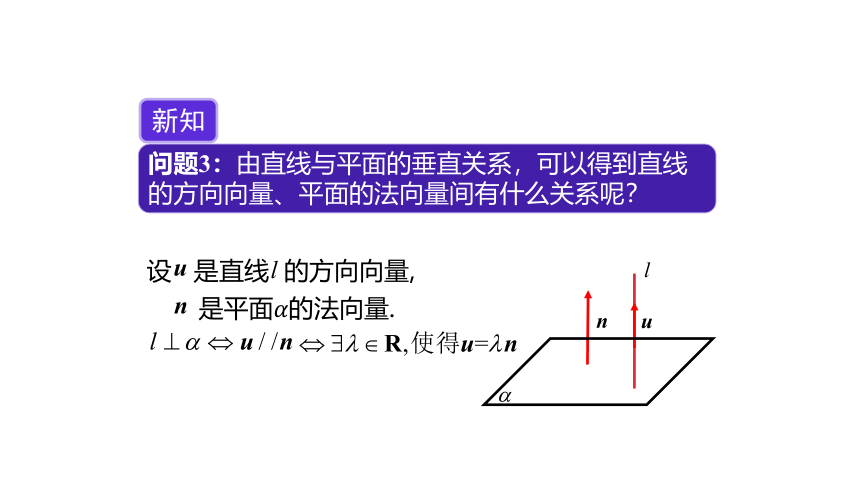
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
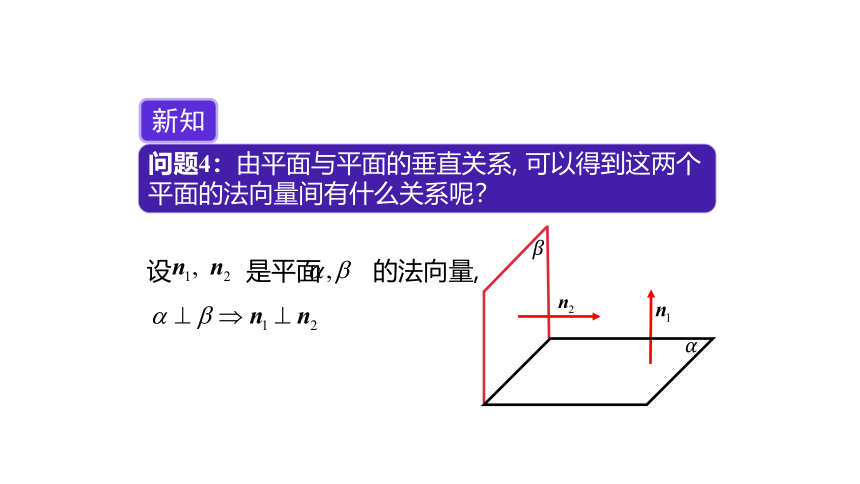
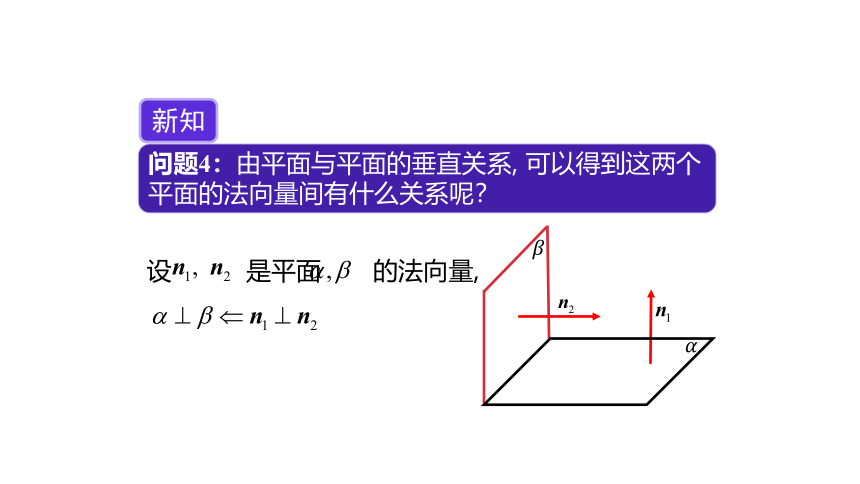
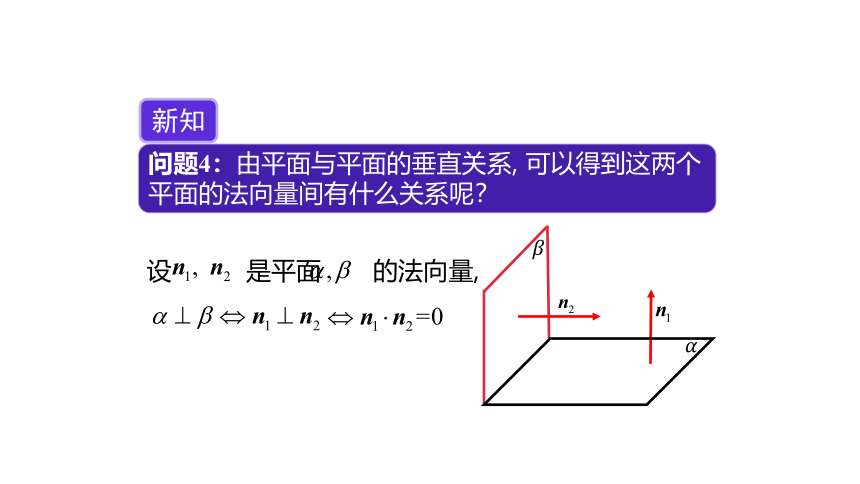
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
追问:我们随时随地看到向量运算的作用. 你同意“向量是躯体,运算是灵魂”“没有运算的向量只能起路标的作用”的说法吗?
新知
新知
点
直线
平面
向量
向量
向量
位置关系
度量问题
位置关系
度量问题
位置关系
度量问题
向量运算
向量运算
向量运算
证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,
求证: .
例题
分析:
因为 ,所以 l 的方向向量u就是平面????的法向量.
?
已知:如图, 求证: .
例题
设平面????的法向量为n.
?
证明:
因为 ,
又因为 , 而n是平面????的法向量,
所以 .
所以
?
即平面????,????的法向量互相垂直.
?
例题
取直线 l 的方向向量u, 平面????的法向量为n.
?
所以u是平面????的法向量.
?
已知:如图, 求证: .
小结
向量法
证明面面垂直
证明法向量垂直
立体几何问题
空间向量问题
转化
还原
例题
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
A1C⊥BD
A1C⊥BB1
其中,n是平面BDD1B1的法向量
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
是平面BDD1B1的法向量
选择合适的基底
表示
运算
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
则 为空间的一个基底.
设 ,
证明:
则 为空间的一个基底.
且
设 ,
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:因为AB= AD =AA1=1,
所以 .
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
则对于平面BDD1B1上任意一点P,
存在唯一的有序实数对 ,
使得 .
在平面BDD1B1上, 取 为基向量,
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:所以
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
所以 是平面 的法向量.
所以 平面 .
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
小结
证明线面垂直
直线的方向向量和平面的法向量平行
直线的方向向量是平面的法向量
平面的向量表示法
直线的方向向量与平面内任意向量的数量积为 0
u//n
例题
小结
向量的运算
向量的坐标运算
利用基底进行向量运算
例题
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
问题5:本节课我们主要学习了哪些知识内容?
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
课堂小结
问题5:本节课我们主要学习了哪些知识内容?
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
向量运算
直线、平面
方向向量、法向量
向量的位置关系
线面的位置关系
向量化
几何化
坐标表示、基向量表示
线面的度量
向量的度量
课堂小结
问题6:本节课的地位和作用是什么?
1. 已知正方体ABCD-A1B1C1D1的棱长为1, 以D为原点, 为单位正交基底建立空间直角坐标系. 求证:A1C⊥BC1.
课后作业
2. 如图,在长方体ABCD-A1B1C1D1中, AB=2, BC=CC1=1, E是CD的中点, F是BC的中点. 求证:平面EAD1⊥平面EFD1 .
课后作业
位置关系(3)
回顾
问题1:由直线、平面的平行关系, 可得直线的方向向量、平面的法向量有什么关系呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题2:由直线与直线的垂直关系, 可以得到这两条直线的方向向量有什么关系呢?
新知
设 分别是直线 的方向向量,
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
问题3:由直线与平面的垂直关系,可以得到直线的方向向量、平面的法向量间有什么关系呢?
新知
设 是直线 的方向向量,
是平面????的法向量.
?
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
问题4:由平面与平面的垂直关系, 可以得到这两个平面的法向量间有什么关系呢?
????
?
????
?
新知
设 是平面 的法向量,
追问:我们随时随地看到向量运算的作用. 你同意“向量是躯体,运算是灵魂”“没有运算的向量只能起路标的作用”的说法吗?
新知
新知
点
直线
平面
向量
向量
向量
位置关系
度量问题
位置关系
度量问题
位置关系
度量问题
向量运算
向量运算
向量运算
证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,
求证: .
例题
分析:
因为 ,所以 l 的方向向量u就是平面????的法向量.
?
已知:如图, 求证: .
例题
设平面????的法向量为n.
?
证明:
因为 ,
又因为 , 而n是平面????的法向量,
所以 .
所以
?
即平面????,????的法向量互相垂直.
?
例题
取直线 l 的方向向量u, 平面????的法向量为n.
?
所以u是平面????的法向量.
?
已知:如图, 求证: .
小结
向量法
证明面面垂直
证明法向量垂直
立体几何问题
空间向量问题
转化
还原
例题
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
A1C⊥BD
A1C⊥BB1
其中,n是平面BDD1B1的法向量
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
分析:
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
例题
直线A1C⊥平面BDD1B1
是平面BDD1B1的法向量
选择合适的基底
表示
运算
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
则 为空间的一个基底.
设 ,
证明:
则 为空间的一个基底.
且
设 ,
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:因为AB= AD =AA1=1,
所以 .
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
则对于平面BDD1B1上任意一点P,
存在唯一的有序实数对 ,
使得 .
在平面BDD1B1上, 取 为基向量,
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:所以
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
证明:
所以 是平面 的法向量.
所以 平面 .
例题
如图, 在平行六面体ABCD-A1B1C1D1中, AB=
AD=AA1=1, .
求证:直线A1C⊥平面BDD1B1.
小结
证明线面垂直
直线的方向向量和平面的法向量平行
直线的方向向量是平面的法向量
平面的向量表示法
直线的方向向量与平面内任意向量的数量积为 0
u//n
例题
小结
向量的运算
向量的坐标运算
利用基底进行向量运算
例题
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
问题5:本节课我们主要学习了哪些知识内容?
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}线面的
位置关系
向量的
位置关系
向量的运算
向量的
坐标运算
课堂小结
问题5:本节课我们主要学习了哪些知识内容?
其中, 分别是直线 的方向向量;
分别是平面 的法向量.
向量运算
直线、平面
方向向量、法向量
向量的位置关系
线面的位置关系
向量化
几何化
坐标表示、基向量表示
线面的度量
向量的度量
课堂小结
问题6:本节课的地位和作用是什么?
1. 已知正方体ABCD-A1B1C1D1的棱长为1, 以D为原点, 为单位正交基底建立空间直角坐标系. 求证:A1C⊥BC1.
课后作业
2. 如图,在长方体ABCD-A1B1C1D1中, AB=2, BC=CC1=1, E是CD的中点, F是BC的中点. 求证:平面EAD1⊥平面EFD1 .
课后作业
