北京市平谷区2020-2021学年高二上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 北京市平谷区2020-2021学年高二上学期期末考试数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 628.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览


文档简介
平谷区2020—2021学年度第一学期质量监控
高二数学试卷 2021.1
考
生
须知
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间为120分钟 .
试题所有答案必须书写在答题卡上,在试卷上作答无效.
考试结束后,将答题卡交回,试卷按学校要求保存好.
第Ⅰ卷(选择题 共40分)
选择题:(本大题共10小题,每小题4分,共40分;在每个小题列出的四个选项中,只有一项是符合要求的.)
直线false经过false两点,那么其斜率false为
A.falsefalse B.false C.false D.false
2. 已知圆的方程false,那么圆心和半径分别为
A.falsefalse B.false
C.falsefalse D.false
3. 抛物线false的焦点到准线的距离是
A.false B.false C.false D. false
4. 双曲线false的离心率false,那么false的值是
A.false B.false C.false D.false
4168775711205. 如图,以长方体false的顶点false为坐标原点,过false的三条棱所在的直线为坐标轴,建立空间直角坐标系,如果false的坐标为false,那么false的坐标是
A.false B.false
C.false D. false
6. 甲、乙两名同学相约学习某种技能,该技能需要通过两项考核才能拿到证书,每项考核结果互不影响.已知甲同学通过第一项考核的概率是false,通过第二项考核的概率是false;乙同学拿到该技能证书的概率是false, 那么甲、乙两人至少有一人拿到该技能证书的概率是
A. false B.false C. false D.false
7. 某校高一年级随机抽取15名男生,测得他们的身高数据,如下表所示:
编号
身高
编号
身高
编号
身高
1
173
6
169
11
168
2
179
7
177
12
175
3
175
8
175
13
172
4
173
9
174
14
169
5
170
10
182
15
176
那么这组数据的第80百分位数是
false B.false C. false D.false
8. 已知椭圆false的右顶点false到双曲线false的一条渐近线距离为false,那么false
false B.false C. false D.false
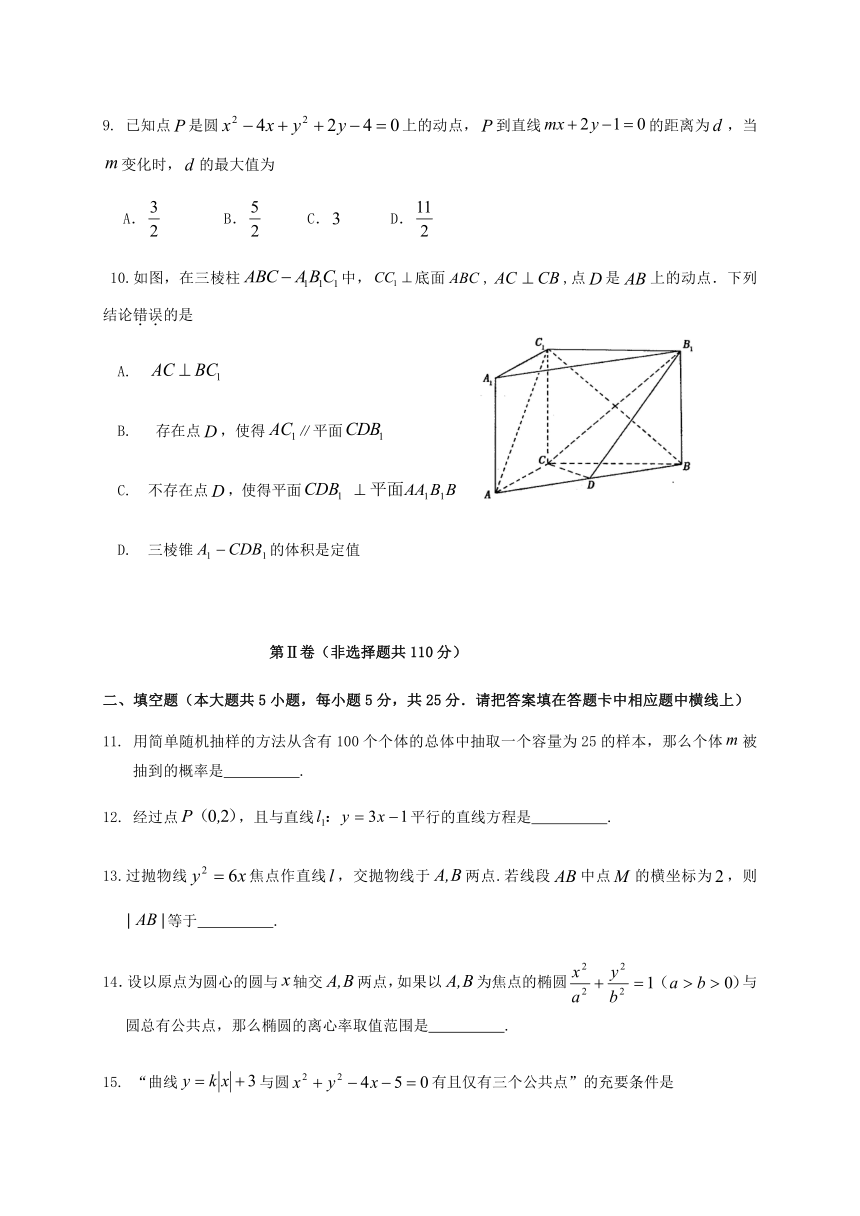
9. 已知点false是圆false上的动点,false到直线false的距离为false,当false变化时,false的最大值为
A.false B.false C.false D.false
3253105652145 10.如图,在三棱柱false中,false底面false,false,点false是false上的动点.下列结论错误的是
A. false
B. 存在点false,使得false∥平面false
C. 不存在点false,使得平面false false
D. 三棱锥false的体积是定值
第Ⅱ卷(非选择题共110分)
二、填空题(本大题共5小题,每小题5分,共25分.请把答案填在答题卡中相应题中横线上)
11. 用简单随机抽样的方法从含有100个个体的总体中抽取一个容量为25的样本,那么个体false被抽到的概率是 .
12. 经过点false,且与直线false平行的直线方程是 .
13.过抛物线false焦点作直线false,交抛物线于false两点.若线段false中点false的横坐标为false,则false等于 .
14.设以原点为圆心的圆与false轴交false两点,如果以false为焦点的椭圆false与圆总有公共点,那么椭圆的离心率取值范围是 .
15. “曲线false与圆false有且仅有三个公共点”的充要条件是
.
三、解答题:(本大题共6小题,共85分;解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分14分)
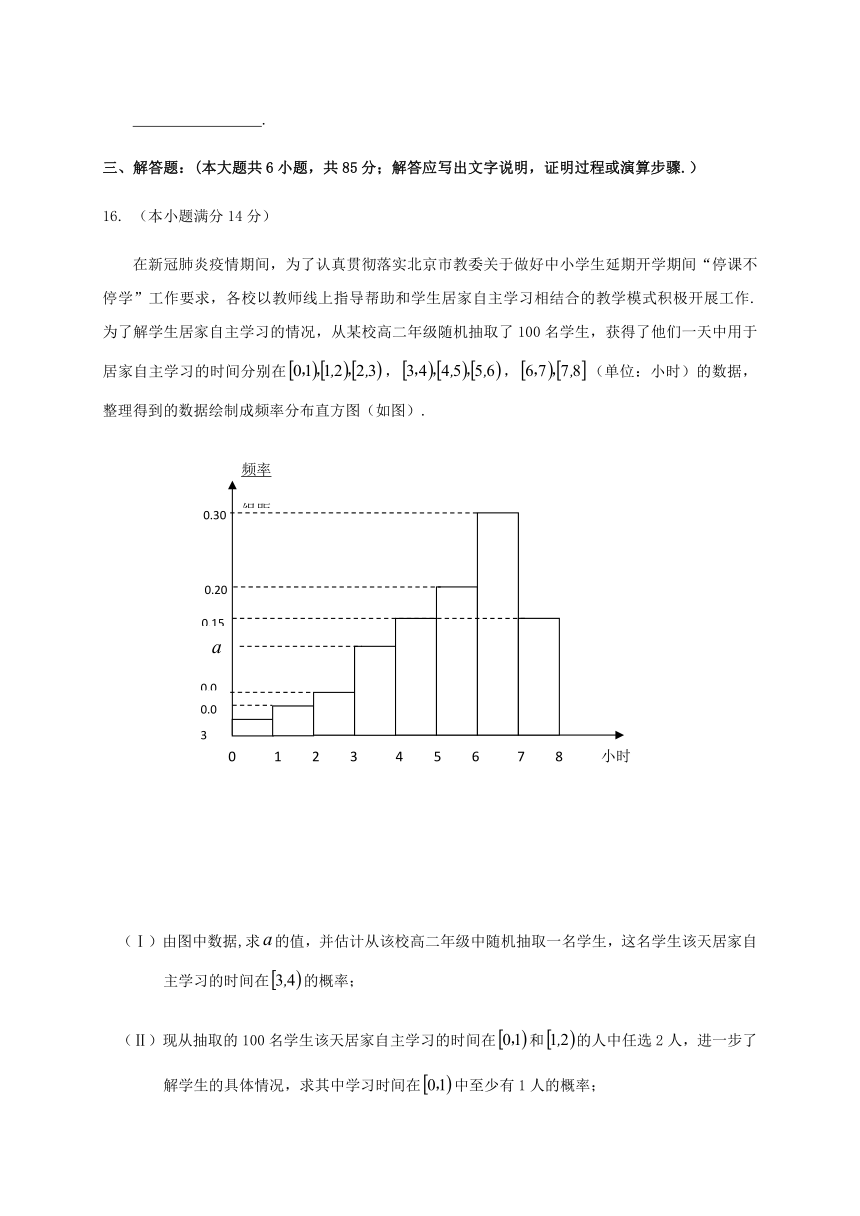
在新冠肺炎疫情期间,为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求,各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况,从某校高二年级随机抽取了100名学生,获得了他们一天中用于居家自主学习的时间分别在false,false,false(单位:小时)的数据,整理得到的数据绘制成频率分布直方图(如图).
765175774700 1 2 3 4 5 6 7 8 小时
频率
组距
0.30
0.20
0.15
false
0.05
0.03
0.02
0 1 2 3 4 5 6 7 8 小时
频率
组距
0.30
0.20
0.15
false
0.05
0.03
0.02
(Ⅰ)由图中数据,求false的值,并估计从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习的时间在false的概率;
(Ⅱ)现从抽取的100名学生该天居家自主学习的时间在false和false的人中任选2人,进一步了解学生的具体情况,求其中学习时间在false中至少有1人的概率;
(III)假设同一时间段中的每个数据可用该时间段的中点值代替,试估计样本中的100名学生该天居家自主学习时间的平均数.
17. (本小题满分14分)
3185795259715false
false
false
false
false
false
false
false
false
false
false
false
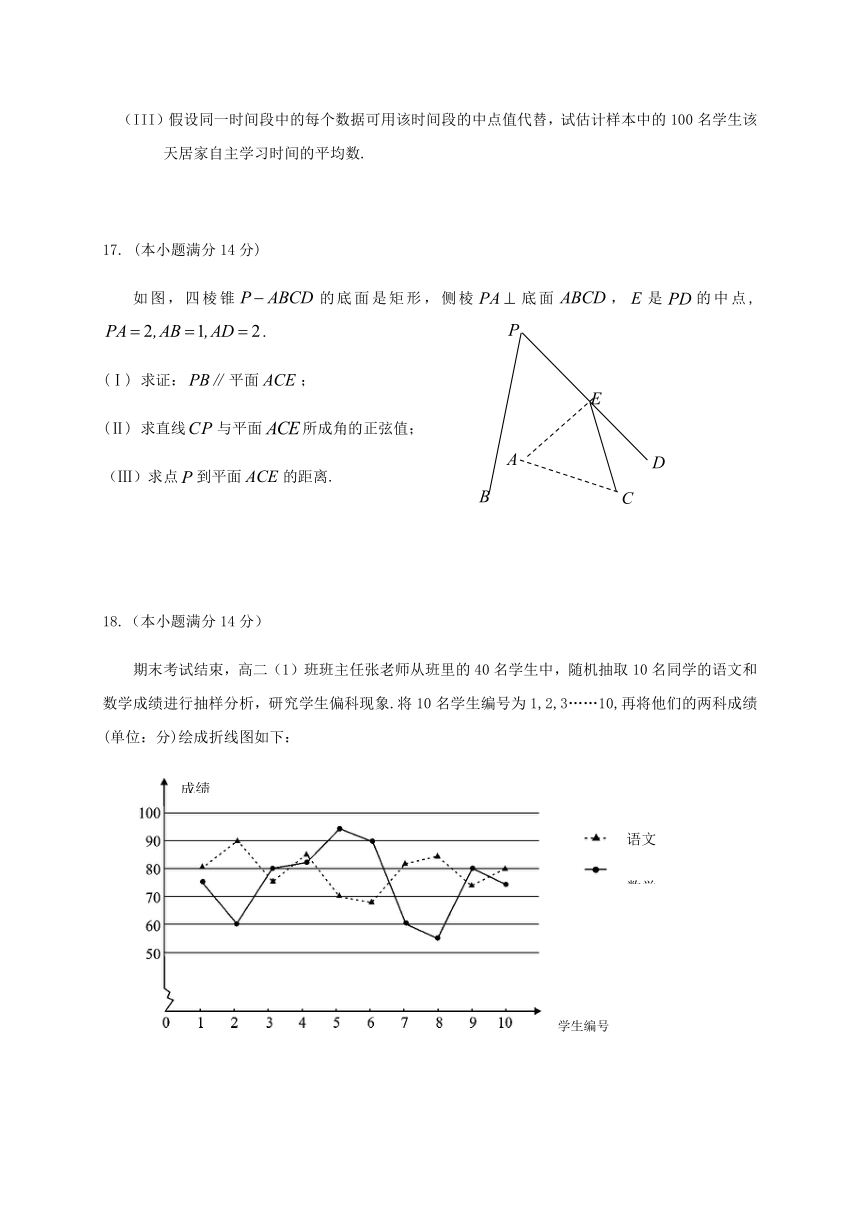
如图,四棱锥的底面是矩形,侧棱底面,是false的中点, false.
3383280278765(Ⅰ) 求证:false平面false;
(Ⅱ) 求直线false与平面false所成角的正弦值;
(Ⅲ)求点false到平面false的距离.
18.(本小题满分14分)
期末考试结束,高二(1)班班主任张老师从班里的40名学生中,随机抽取10名同学的语文和数学成绩进行抽样分析,研究学生偏科现象.将10名学生编号为1,2,3……10,再将他们的两科成绩(单位:分)绘成折线图如下:
58864517145语文
数学
成绩
学生编号
语文
数学
成绩
学生编号
31750085725
(Ⅰ)从这10名学生中随机抽取一名学生,求抽取的这名学生两科成绩相差大于10分的概率;
(Ⅱ)从两科成绩均超过70分的学生中随机抽取2人进行访谈,求这2人中恰有一个是语文成绩高于数学成绩的概率;
(Ⅲ)设该班语文和数学两科成绩的平均值分别为false,方差分别为false,根据折线图,试推断false和false,false和false的大小关系(直接写出结论,不需证明)。
19.(本小题满分14分)
如图,平面false⊥平面false,四边形false是边长为false的正方形,false,false,false为false的中点,点false在线段false上.
(Ⅰ)求证:false平面false;
(Ⅱ)若存在点false,使得平面false与平面false所成二面角的余弦值为false,求false的值.
307340011430false
false
false
false
false
false
false
false
false
false
false
false
false
false
20. (本小题满分14分)
已知椭圆false的离心率false,且过点false.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设椭圆右顶点为false,直线false过点false,且与椭圆交于另一点false(不同于false点),若有false,求直线false方程.
21.(本小题满分15分)
已知椭圆false:false的左、右焦点分别为false,false,点false在椭圆上.
(Ⅰ)求椭圆false的标准方程;
(Ⅱ)若直线false与圆false相切,且与椭圆false交于不同的两点false,设false,求false的取值范围.
平谷区2020—2021学年第一学期质量监控
高二数学 2021、1
一、选择题:(本大题共8小题,每小题5分,共40分.)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
B
C
A
D
C
B
D
C
二、填空题(本大题共5小题,每小题5分,共25分.)
11. false 12. false 13. 7 14. false 15. false
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. (本小题满分14分)
解:(Ⅰ)因为false,
所以false. ……………3分
由图可得:随机抽取的100名学生中居家自主学习时间该天在false的频率为false,
所以从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习时间在false的概率为false. …………5分
(Ⅱ)设“抽取的2人其中学习时间在false中至少有1人”为事件A ……6分
由图中数据可知:该天居家自主学习时间在false和false的人分别有2人和3人. ……………7分
设在false的2人分别为false,在false的3人分别false……………8分
则从这5人中任选2人的样本空间false共有10个样本点
事件Afalse ,共有7个样本点…………10分
false
所以学习时间在false中至少有1人的 概率为false ………… 11分
(III)样本平均数:
falsefalse.
样本中的100名学生该天居家自主学习时间的平均数为5.38小时. ………14分
17. (本小题满分14分)
解: (Ⅰ)证明:连结false交false于false,连结false,
因为四边形false是矩形,所以false为false中点.
又因为false是false的中点,所以false, ………2分
因为false平面false,false平面false,
所以false平面false ……………4分
解法二:
(Ⅰ)证明:解:四棱锥的底面是矩形,侧棱底面,因此以false为原点,以false为false轴,以false为false轴,建立空间直角坐标系.
所以false,false,false,false,false………2分
设平面false的一个法向量为false……………3分
false,即:false……………5分
因为false,所以false……………6分
又因为false平面false,所以false平面false.……………7分
(Ⅱ) 设直线false与平面false所成角为false,
由false,平面false的一个法向量为false
所以falsefalse,
即直线false与平面false所成角的正弦值为false.……………11分
(Ⅲ)设点false到平面false的距离false,则false
所以点false到平面的距离false……………14分
18.(本小题满分14分)
解:(Ⅰ)设“抽取的这名学生两科成绩相差大于10分”为事件false………1分
由图可得数学、语文成绩相差大于10分的学生编号分别是2,5,6,7,8,共有5人,所以false………4分
(Ⅱ)设“抽取的这2人中恰有一个是语文成绩高于数学成绩”为事件false………5分
因为两科成绩均超过70分的学生编号分别是1,3,4,9,10,则构成的样本空间
false共10个样本点
事件false包含false共6个样本点………9分
所以这2人中恰有一个是语文成绩高于数学成绩的概率false;………10分
(Ⅲ)false,false ………14分
19.(本小题满分14分)
解:
(Ⅰ)证明:因为正方形false,
所以false.
因为平面false⊥平面false,且平面false平面false,
所以false平面false. ……………………2分
因为false平面false,
所以false.
因为false,false为false的中点,
所以false,且false,
所以false平面false. ……………………5分
解法二:
(Ⅰ)因为正方形false,
所以false.
因为平面false⊥平面false,且平面false平面false,
所以false平面false. ……………………2分
所以false
因为false所以false互相垂直.
以false为原点,以false分别为false轴建立空间直角坐标系
由题意false,false,false,false,false.………………4分
所以false,false,false.
因为false
即false
false
所以false平面false. ……………………6分
(Ⅱ)因为点false在线段false上,设false.
所以存在false,使得false.
因为false,false,
所以false, 所以false.
所以false, ……………………8分
设平面false的一个法向量为false,
则false, 即false.
所以false. ……………………10分
因为false平面false,
所以平面false的一个法向量是false,……………………11分
又因为平面false与平面false所成二面角的余弦值为false,
所以false, ……13分
所以false或false舍去. 所以false. …………14分
20. (本小题满分14分)
解:(Ⅰ)由椭圆方程可知,椭圆焦点在false轴,
因为离心率false,且过点false.
所以false,…………4分
所以椭圆的标准方程false…………5分
(Ⅱ)解法一:当直线false斜率不存在时,false,又椭圆右顶点为false
此时false,不满足false.…………6分
因此设直线falsefalse,false …………7分
false
因为false,所以false…………10分
因为false,false所以 false …………11分
即false整理得false
解得:false或者false(false与false重合,舍)…………13分
所以直线false:false …………14分
解法二:因为false,false所以false…………6分
因此设直线false …………7分
false …………9分
设false,又椭圆右顶点为false …………10分
所以false,false即false…………12分
得false
因此直线false:false …………14分
21.(本小题满分15分)
解:(Ⅰ)
解法1:根据题意
false,
根据椭圆的定义得 false,所以false.……………………3分
因为椭圆的左、右焦点分别为false,false,
由 所以false.
所以椭圆的标准方程为 false. ……………………5分
解法2:根据题意可知:false轴,
在直角三角形false中,由false,false,解得false
即false ,所以false.……………………3分
因为椭圆的左、右焦点分别为false,false,
由 所以false.
所以椭圆的标准方程为 false. ……………………5分
(Ⅱ)若直线false的斜率不存在,则直线方程为false或false.
当false时,false,false,
此时false.
同理当false时,false.
所以当直线false的斜率不存在时false. ………………7分
若直线false的斜率存在,设直线false:false,与椭圆交点 false,false.
因为直线false和圆相切,所以 false,
化简得false. ……………………9分
联立方程false, 消false得false,
显然false.
所以 false,false.……………………12分
因此false
false
false
由false代入得:
false ………………13分
因为false,所以 false. ………………14分
综上所述,false. ……………………15分
(若用其他方法解题,请酌情给分)
高二数学试卷 2021.1
考
生
须知
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间为120分钟 .
试题所有答案必须书写在答题卡上,在试卷上作答无效.
考试结束后,将答题卡交回,试卷按学校要求保存好.
第Ⅰ卷(选择题 共40分)
选择题:(本大题共10小题,每小题4分,共40分;在每个小题列出的四个选项中,只有一项是符合要求的.)
直线false经过false两点,那么其斜率false为
A.falsefalse B.false C.false D.false
2. 已知圆的方程false,那么圆心和半径分别为
A.falsefalse B.false
C.falsefalse D.false
3. 抛物线false的焦点到准线的距离是
A.false B.false C.false D. false
4. 双曲线false的离心率false,那么false的值是
A.false B.false C.false D.false
4168775711205. 如图,以长方体false的顶点false为坐标原点,过false的三条棱所在的直线为坐标轴,建立空间直角坐标系,如果false的坐标为false,那么false的坐标是
A.false B.false
C.false D. false
6. 甲、乙两名同学相约学习某种技能,该技能需要通过两项考核才能拿到证书,每项考核结果互不影响.已知甲同学通过第一项考核的概率是false,通过第二项考核的概率是false;乙同学拿到该技能证书的概率是false, 那么甲、乙两人至少有一人拿到该技能证书的概率是
A. false B.false C. false D.false
7. 某校高一年级随机抽取15名男生,测得他们的身高数据,如下表所示:
编号
身高
编号
身高
编号
身高
1
173
6
169
11
168
2
179
7
177
12
175
3
175
8
175
13
172
4
173
9
174
14
169
5
170
10
182
15
176
那么这组数据的第80百分位数是
false B.false C. false D.false
8. 已知椭圆false的右顶点false到双曲线false的一条渐近线距离为false,那么false
false B.false C. false D.false
9. 已知点false是圆false上的动点,false到直线false的距离为false,当false变化时,false的最大值为
A.false B.false C.false D.false
3253105652145 10.如图,在三棱柱false中,false底面false,false,点false是false上的动点.下列结论错误的是
A. false
B. 存在点false,使得false∥平面false
C. 不存在点false,使得平面false false
D. 三棱锥false的体积是定值
第Ⅱ卷(非选择题共110分)
二、填空题(本大题共5小题,每小题5分,共25分.请把答案填在答题卡中相应题中横线上)
11. 用简单随机抽样的方法从含有100个个体的总体中抽取一个容量为25的样本,那么个体false被抽到的概率是 .
12. 经过点false,且与直线false平行的直线方程是 .
13.过抛物线false焦点作直线false,交抛物线于false两点.若线段false中点false的横坐标为false,则false等于 .
14.设以原点为圆心的圆与false轴交false两点,如果以false为焦点的椭圆false与圆总有公共点,那么椭圆的离心率取值范围是 .
15. “曲线false与圆false有且仅有三个公共点”的充要条件是
.
三、解答题:(本大题共6小题,共85分;解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分14分)
在新冠肺炎疫情期间,为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求,各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况,从某校高二年级随机抽取了100名学生,获得了他们一天中用于居家自主学习的时间分别在false,false,false(单位:小时)的数据,整理得到的数据绘制成频率分布直方图(如图).
765175774700 1 2 3 4 5 6 7 8 小时
频率
组距
0.30
0.20
0.15
false
0.05
0.03
0.02
0 1 2 3 4 5 6 7 8 小时
频率
组距
0.30
0.20
0.15
false
0.05
0.03
0.02
(Ⅰ)由图中数据,求false的值,并估计从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习的时间在false的概率;
(Ⅱ)现从抽取的100名学生该天居家自主学习的时间在false和false的人中任选2人,进一步了解学生的具体情况,求其中学习时间在false中至少有1人的概率;
(III)假设同一时间段中的每个数据可用该时间段的中点值代替,试估计样本中的100名学生该天居家自主学习时间的平均数.
17. (本小题满分14分)
3185795259715false
false
false
false
false
false
false
false
false
false
false
false
如图,四棱锥的底面是矩形,侧棱底面,是false的中点, false.
3383280278765(Ⅰ) 求证:false平面false;
(Ⅱ) 求直线false与平面false所成角的正弦值;
(Ⅲ)求点false到平面false的距离.
18.(本小题满分14分)
期末考试结束,高二(1)班班主任张老师从班里的40名学生中,随机抽取10名同学的语文和数学成绩进行抽样分析,研究学生偏科现象.将10名学生编号为1,2,3……10,再将他们的两科成绩(单位:分)绘成折线图如下:
58864517145语文
数学
成绩
学生编号
语文
数学
成绩
学生编号
31750085725
(Ⅰ)从这10名学生中随机抽取一名学生,求抽取的这名学生两科成绩相差大于10分的概率;
(Ⅱ)从两科成绩均超过70分的学生中随机抽取2人进行访谈,求这2人中恰有一个是语文成绩高于数学成绩的概率;
(Ⅲ)设该班语文和数学两科成绩的平均值分别为false,方差分别为false,根据折线图,试推断false和false,false和false的大小关系(直接写出结论,不需证明)。
19.(本小题满分14分)
如图,平面false⊥平面false,四边形false是边长为false的正方形,false,false,false为false的中点,点false在线段false上.
(Ⅰ)求证:false平面false;
(Ⅱ)若存在点false,使得平面false与平面false所成二面角的余弦值为false,求false的值.
307340011430false
false
false
false
false
false
false
false
false
false
false
false
false
false
20. (本小题满分14分)
已知椭圆false的离心率false,且过点false.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设椭圆右顶点为false,直线false过点false,且与椭圆交于另一点false(不同于false点),若有false,求直线false方程.
21.(本小题满分15分)
已知椭圆false:false的左、右焦点分别为false,false,点false在椭圆上.
(Ⅰ)求椭圆false的标准方程;
(Ⅱ)若直线false与圆false相切,且与椭圆false交于不同的两点false,设false,求false的取值范围.
平谷区2020—2021学年第一学期质量监控
高二数学 2021、1
一、选择题:(本大题共8小题,每小题5分,共40分.)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
B
C
A
D
C
B
D
C
二、填空题(本大题共5小题,每小题5分,共25分.)
11. false 12. false 13. 7 14. false 15. false
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. (本小题满分14分)
解:(Ⅰ)因为false,
所以false. ……………3分
由图可得:随机抽取的100名学生中居家自主学习时间该天在false的频率为false,
所以从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习时间在false的概率为false. …………5分
(Ⅱ)设“抽取的2人其中学习时间在false中至少有1人”为事件A ……6分
由图中数据可知:该天居家自主学习时间在false和false的人分别有2人和3人. ……………7分
设在false的2人分别为false,在false的3人分别false……………8分
则从这5人中任选2人的样本空间false共有10个样本点
事件Afalse ,共有7个样本点…………10分
false
所以学习时间在false中至少有1人的 概率为false ………… 11分
(III)样本平均数:
falsefalse.
样本中的100名学生该天居家自主学习时间的平均数为5.38小时. ………14分
17. (本小题满分14分)
解: (Ⅰ)证明:连结false交false于false,连结false,
因为四边形false是矩形,所以false为false中点.
又因为false是false的中点,所以false, ………2分
因为false平面false,false平面false,
所以false平面false ……………4分
解法二:
(Ⅰ)证明:解:四棱锥的底面是矩形,侧棱底面,因此以false为原点,以false为false轴,以false为false轴,建立空间直角坐标系.
所以false,false,false,false,false………2分
设平面false的一个法向量为false……………3分
false,即:false……………5分
因为false,所以false……………6分
又因为false平面false,所以false平面false.……………7分
(Ⅱ) 设直线false与平面false所成角为false,
由false,平面false的一个法向量为false
所以falsefalse,
即直线false与平面false所成角的正弦值为false.……………11分
(Ⅲ)设点false到平面false的距离false,则false
所以点false到平面的距离false……………14分
18.(本小题满分14分)
解:(Ⅰ)设“抽取的这名学生两科成绩相差大于10分”为事件false………1分
由图可得数学、语文成绩相差大于10分的学生编号分别是2,5,6,7,8,共有5人,所以false………4分
(Ⅱ)设“抽取的这2人中恰有一个是语文成绩高于数学成绩”为事件false………5分
因为两科成绩均超过70分的学生编号分别是1,3,4,9,10,则构成的样本空间
false共10个样本点
事件false包含false共6个样本点………9分
所以这2人中恰有一个是语文成绩高于数学成绩的概率false;………10分
(Ⅲ)false,false ………14分
19.(本小题满分14分)
解:
(Ⅰ)证明:因为正方形false,
所以false.
因为平面false⊥平面false,且平面false平面false,
所以false平面false. ……………………2分
因为false平面false,
所以false.
因为false,false为false的中点,
所以false,且false,
所以false平面false. ……………………5分
解法二:
(Ⅰ)因为正方形false,
所以false.
因为平面false⊥平面false,且平面false平面false,
所以false平面false. ……………………2分
所以false
因为false所以false互相垂直.
以false为原点,以false分别为false轴建立空间直角坐标系
由题意false,false,false,false,false.………………4分
所以false,false,false.
因为false
即false
false
所以false平面false. ……………………6分
(Ⅱ)因为点false在线段false上,设false.
所以存在false,使得false.
因为false,false,
所以false, 所以false.
所以false, ……………………8分
设平面false的一个法向量为false,
则false, 即false.
所以false. ……………………10分
因为false平面false,
所以平面false的一个法向量是false,……………………11分
又因为平面false与平面false所成二面角的余弦值为false,
所以false, ……13分
所以false或false舍去. 所以false. …………14分
20. (本小题满分14分)
解:(Ⅰ)由椭圆方程可知,椭圆焦点在false轴,
因为离心率false,且过点false.
所以false,…………4分
所以椭圆的标准方程false…………5分
(Ⅱ)解法一:当直线false斜率不存在时,false,又椭圆右顶点为false
此时false,不满足false.…………6分
因此设直线falsefalse,false …………7分
false
因为false,所以false…………10分
因为false,false所以 false …………11分
即false整理得false
解得:false或者false(false与false重合,舍)…………13分
所以直线false:false …………14分
解法二:因为false,false所以false…………6分
因此设直线false …………7分
false …………9分
设false,又椭圆右顶点为false …………10分
所以false,false即false…………12分
得false
因此直线false:false …………14分
21.(本小题满分15分)
解:(Ⅰ)
解法1:根据题意
false,
根据椭圆的定义得 false,所以false.……………………3分
因为椭圆的左、右焦点分别为false,false,
由 所以false.
所以椭圆的标准方程为 false. ……………………5分
解法2:根据题意可知:false轴,
在直角三角形false中,由false,false,解得false
即false ,所以false.……………………3分
因为椭圆的左、右焦点分别为false,false,
由 所以false.
所以椭圆的标准方程为 false. ……………………5分
(Ⅱ)若直线false的斜率不存在,则直线方程为false或false.
当false时,false,false,
此时false.
同理当false时,false.
所以当直线false的斜率不存在时false. ………………7分
若直线false的斜率存在,设直线false:false,与椭圆交点 false,false.
因为直线false和圆相切,所以 false,
化简得false. ……………………9分
联立方程false, 消false得false,
显然false.
所以 false,false.……………………12分
因此false
false
false
由false代入得:
false ………………13分
因为false,所以 false. ………………14分
综上所述,false. ……………………15分
(若用其他方法解题,请酌情给分)
同课章节目录
