直线与圆的位置关系

(共18张PPT)
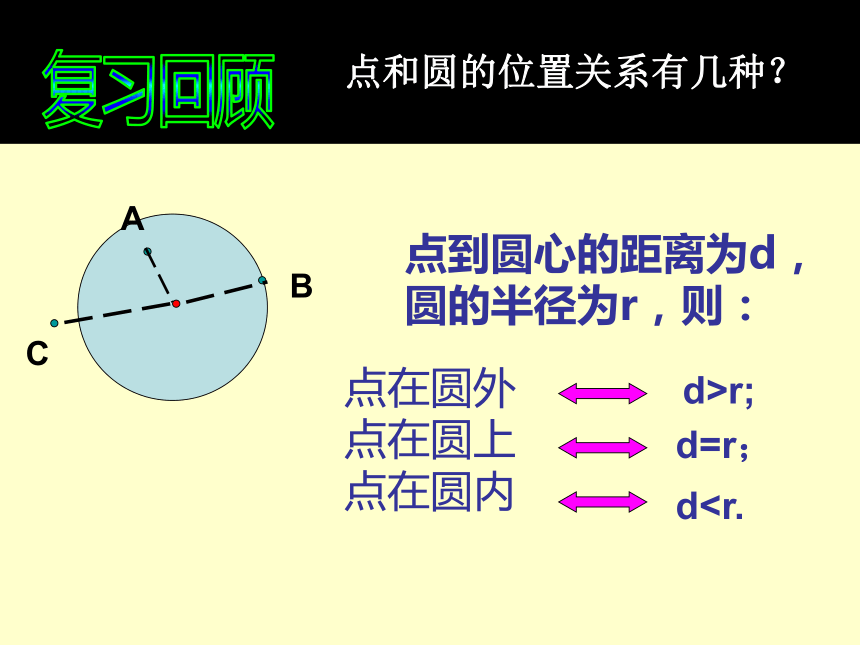
点和圆的位置关系有几种？
点到圆心的距离为d，圆的半径为r，则：
点在圆外
点在圆上
点在圆内
A
B
C
d>r;
d=r；
d直线与圆的位置关系
(地平线)
a(地平线)
●O
●O
●O
●O
●O
特点：
叫做直线和圆相交。
直线和圆有两个公共点，
特点：
直线和圆有惟一的公共点，
叫做直线和圆相切。
这时的直线叫切线
惟一的公共点叫切点。
特点：
直线和圆没有公共点，
叫直线和圆相离
一、直线与圆的位置关系
（用公共点的个数来区分）
.A
.A
.B
C
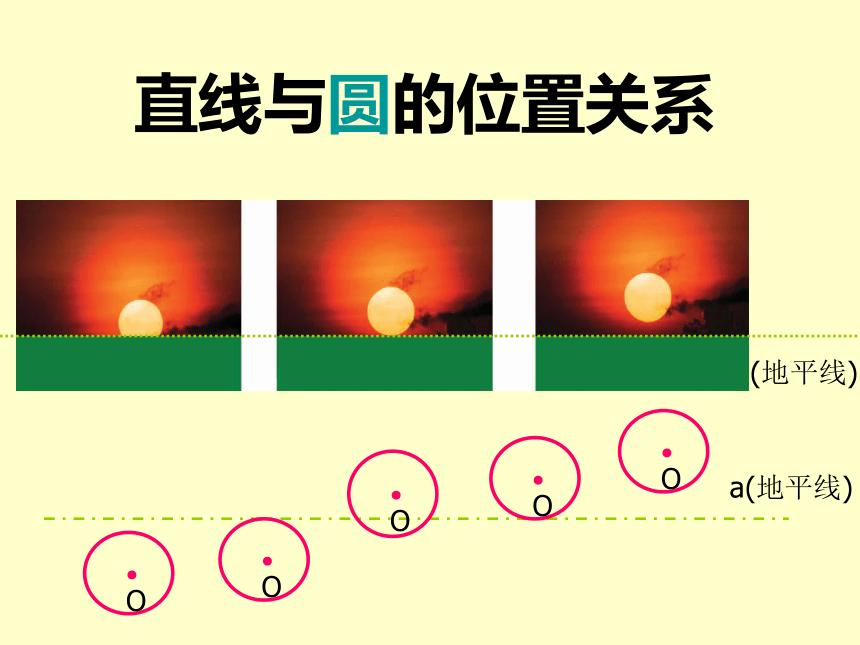
观察太阳落山的照片,在太阳落山的过程中,太阳与地平线(直线a)经历了哪些位置关系的变化
a(地平线)
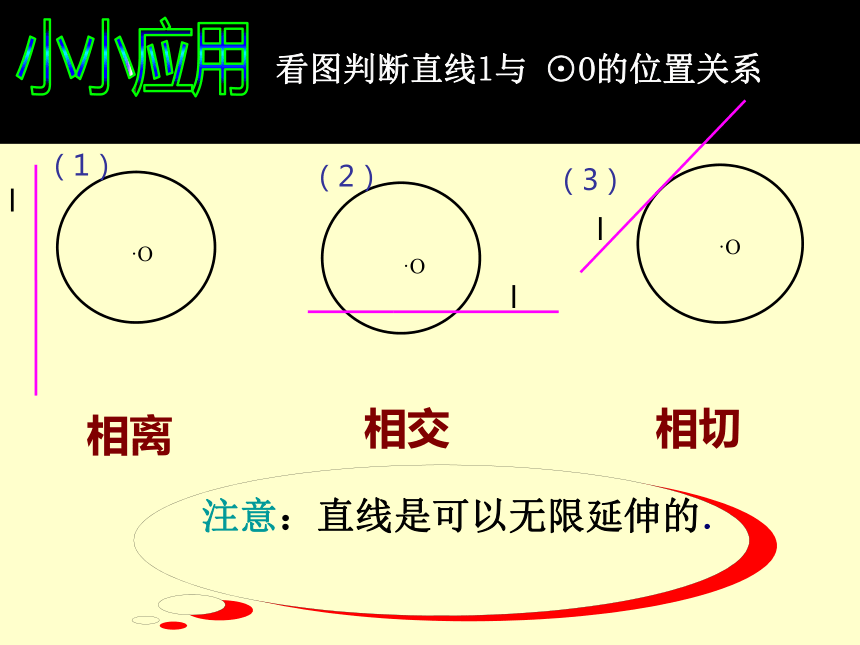
看图判断直线l与 ⊙O的位置关系
（1）
（3）
（2）
相离
l
l
l
·O
·O
·O
相交
注意：直线是可以无限延伸的．
相切
．Ｏ
l
┐
d
．ｏ
l
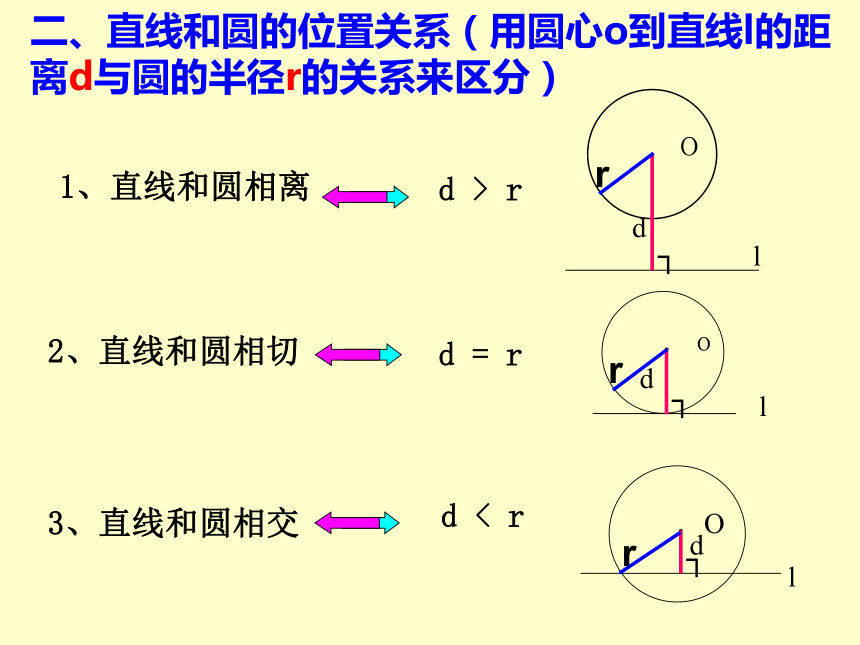
2、直线和圆相切
┐
d
d = r
．O
l
3、直线和圆相交
d < r
d
┐
二、直线和圆的位置关系（用圆心o到直线l的距离d与圆的半径r的关系来区分）
1、直线和圆相离
d > r
r
r
r
1、已知圆的直径为13cm，设直线和圆心的距离
　为d ：
3)若d= 8 cm ,则直线与圆______,
直线与圆有____个公共点.
若d=6.5cm ,则直线与圆______,
直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆　　　,
直线与圆有____个公共点.
相交
相切
相离
课堂练习：
2
1
0
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
d > 5cm
d = 5cm
d < 5cm
课堂练习：
如图,在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系 为什么
(1) r=2 (2) r=2 (3) r=3
450
4
D
2
450
4
D
2
450
4
D
2
相离
相切
相交
分析：因为题目中给出了⊙C的半径，所以关键是求出圆心C到直线AB的距离。因此，可过点C作CD⊥AB，垂足为D。求出CD的长，把CD的长与⊙C的半径r进行比较，就可判断⊙C和AB的位置关系。
当堂检测：
1.判断正误
1)与圆有公共点的直线是圆的切线 ( )
2)过圆外一点画一条直线,则直线与圆相离( )
3)过圆内一点画一条直线,则直线与圆相交( )
×
×
√
2. 设⊙O的半径为3，直线a上一点到圆心的距离为3，则直线a与⊙O的位置关系是（ ）
（A）相交 （B）相切
（C）相离 （D）相切或相交
D
A.(-3,-4)
O
x
y
拓展:已知⊙A的直径为6，点A的坐标为（-3，-4），则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。
B
C
4
3
相离
相切
-1
-1
.(-3,-4)
O
x
y
B
C
4
3
-1
-1
思考:若⊙A要与x轴相切，则⊙A该向上移动多少个单位？若⊙A要与x轴相交呢？
0
d>r
1
d=r
切点
切线
2
d．Ｏ
l
d
r
┐
┐
．ｏ
l
d
r
．O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
交 点
割 线
2、判定直线 与圆的位置关系的方法有____种：
（1）根据定义，由__________________的个数来判断；
（2）根据性质，由_____________________ ______________的关系来判断．
在实际应用中，常采用第二种方法判定．
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
讨论
D
　在Rt△ABC中，∠C=90°，AC=5cm，BC=12cm，
以C为圆心，r为半径作圆。
①当r满足　　　　　 时， 直线ＡＢ与⊙Ｃ相离。
②当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相切。
③当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相交。
12
B
C
A
13
0﹤r﹤
r=
r﹥
④当r满足 时,
线段ＡＢ与⊙Ｃ只有一个公共点。
或5﹤r≤12
r=
5
CD= cm
(1)当r= 时,⊙O上有且只有1个点到直线l的距离为3;
在同一平面内,已知点O到直线l的距离为5.以点O为圆心,r为半径画圆.
(2)当r= 时, ⊙O上有且只有3个点到直线l的距离为3;
(3)随着r的变化, ⊙O上到直线l的距离等于3的点的个数有那些变化
下课了!
作业：习题24.2 第2题