人教版 七年级数学下册 第五章 相交线与平行线 5.3.1 平行线的性质 课后练习 (Word版 含答案)
文档属性
| 名称 | 人教版 七年级数学下册 第五章 相交线与平行线 5.3.1 平行线的性质 课后练习 (Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 384.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 06:03:25 | ||
图片预览



文档简介
人教版七年级数学下册
第五章
相交线与平行线
5.3.1
平行线的性质
课后练习2
一、选择题
1.如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为(
)
A.20°
B.25°
C.35°
D.50°
2.如图,直线、相交于点,.若,则等于(
)
A.70°
B.110°
C.90°
D.120°
3.如图,直线,直线与,分别相交于,两点,过点作直线的垂线交直线于点,若,则的度数为(
)
A.
B.
C.
D.
4.如图,直线与直线相交,已知,则的度数为(
)
A.
B.
C.
D.
5.如图,若,则图中与互补的角有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于( )
A.70°
B.80°
C.90°
D.100°
7.如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )
A.70°
B.45°
C.110°
D.135°
8.如图,已知AB∥CD,BE和DF分别平分∠ABF和∠CDE,2∠E-∠F=48°,则∠CDE的度数为(
).
A.16°
B.32°
C.48°
D.64°
9.如图,直线,点在上,点、点在上,的角平分线交于点,过点作于点,已知,则的度数为(
)
A.26?
B.32?
C.36?
D.42?
10.如图,BD是△ABC的角平分线,DE∥BC,DE交AB于E,若AB=BC,则下列结论中错误的是(
)
A.BD⊥AC
B.∠A=∠EDA
C.2AD=BC
D.BE=ED
二、填空题
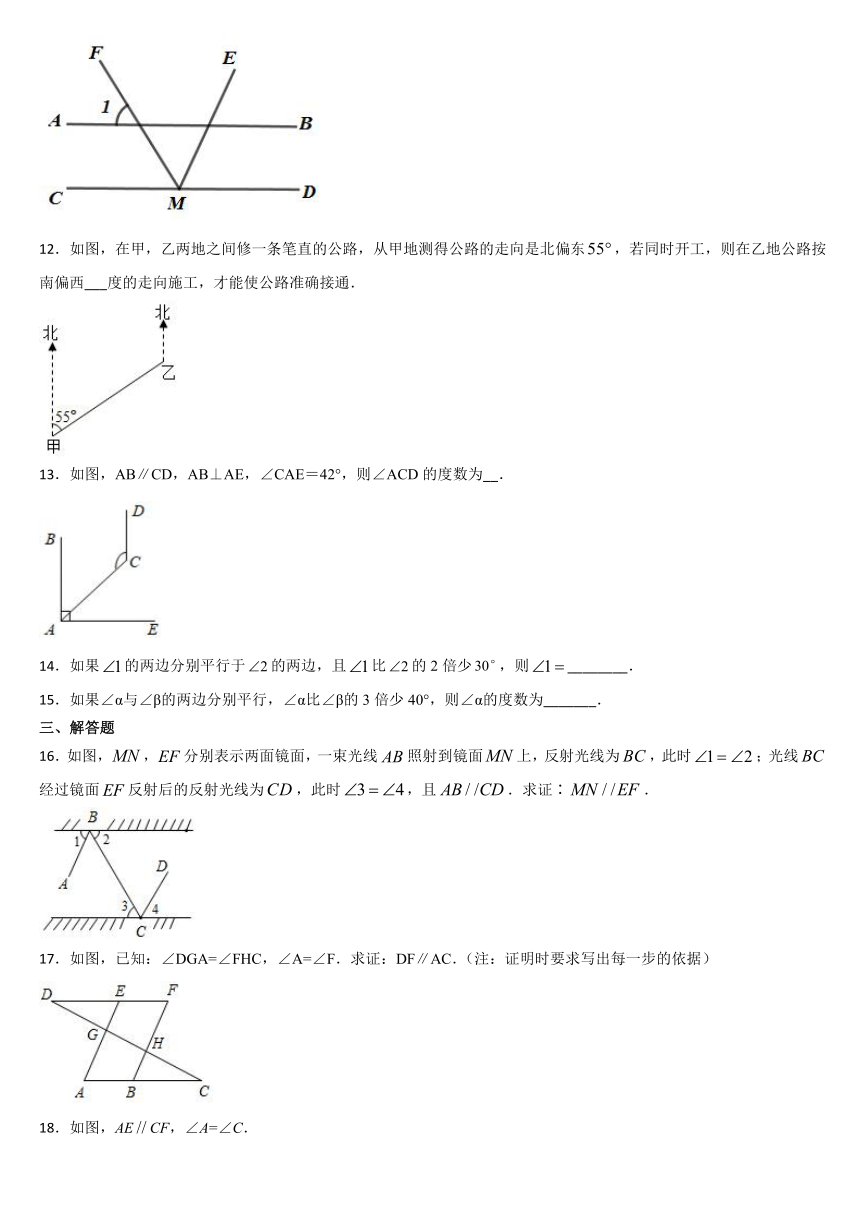
11.如图,,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为_____度.
12.如图,在甲,乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东,若同时开工,则在乙地公路按南偏西___度的走向施工,才能使公路准确接通.
13.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为__.
14.如果的两边分别平行于的两边,且比的2倍少,则________.
15.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为_______.
三、解答题
16.如图,,分别表示两面镜面,一束光线照射到镜面上,反射光线为,此时;光线经过镜面反射后的反射光线为,此时,且.求证∶.
17.如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据)
18.如图,AECF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由.
19.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠ABN的度数是_____,∠CBD的度数是_______;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是多少?
20.如图,∠1=∠2,∠3=∠4,∠5=∠6,求证:AD∥BC
21.已知:如图(1),直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.(1)求∠EKF的度数.(计算过程不准用三角形内角和)(2)如图(2),∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)
22.如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC+∠PAB+∠PCD=
;
(2)图②中,
;
(3)图③中,写出∠APC与∠PAB,∠PCD的三者数量关系,并说明理由
23.(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD
°.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
【参考答案】
1.A
2.B
3.D
4.B
5.D
6.B
7.C
8.B
9.A
10.C
11.
12.55
13.132°
14.或
15.或
16.解:证明:∵,
∴,
又∵,
∴,
又∵,,
∴,
∴.
17.证明:∵∠DGA=∠EGC(对顶角相等)
又∵∠DGA=∠FHC(已知)
∴∠EGC=∠FHC(等量代换)
∴AE∥BF
(同位角相等,两直线平行)
∴∠A=∠FBC
(两直线平行,同位角相等)
又∵∠A=∠F(已知)
∴∠F=∠FBC
(等量代换)
∴DF∥AC
(内错角相等,两直线平行).
18.解:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,
∴∠A+∠ADC=180°,
又∵∠A=∠C,
∴∠C+∠ADC=180°,
∴BC∥AD.
19.(1)∵AM//BN,∠A=64°,
∴∠ABN=180°﹣∠A=116°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=116°,
∴∠CBD=∠CBP+∠DBP=58°;
故答案为:116°;58°;
(2)不变,∠APB=2∠ADB,
∵AM//BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AM//BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN
∴∠ABC=∠DBN,
由(1)∠ABN=116°,
∴∠CBD=58°,
∴∠ABC+∠DBN=58°,
∴∠ABC=29°.
20.∵∠5=∠6
∴AB∥CD
∴∠4+∠BAE=180°
∴∠4+∠2+∠5=180°
∵∠3=∠4,∠1=∠2
∴∠3+∠1+∠5=180°
∴∠5+∠ABC=180°
∴AD∥BC
21.(1)过K作KG∥AB,可得KG∥CD,如图所示:
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°-(∠KEF+∠EFK)-(∠KEK1+∠KFK1)=45°,则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=
×90°。
点睛:解本题主要运用了平行线的性质,角平分线定义,属于探究型试题,熟练掌握平行线的性质是解本题的关键。
22.三个图形中过P作PE与AB平行,由AB与CD平行,利用平行于同一条直线的两直线平行得到PE与CD平行,利用平行线的性质判断即可得到结果.
试题解析:(1)过P作PE∥AB,如图①
∵AB∥CD,
∴PE∥CD,
∴∠A+∠APE=180°,∠EPC+∠C=180°,
∴∠APC+∠PAB+∠PCD=∠A+∠APE+∠EPC+∠C=360°;
(2)过P作PE∥AB,如图②
∵AB∥CD,
∴PE∥CD,
∴∠A=∠APE,∠EPC=∠C,
∴∠APC=∠APE+∠EPC=∠PAB+∠PCD;
(3)∠APC=∠PCD-∠PAB,
理由为:过P作PE∥AB,如图③
∵AB∥CD,
∴PE∥CD,
∴∠PAB+∠APE=180°,∠EPC+∠PCD=180°,
即∠APE=180°-∠PAB,∠EPC=180°-∠PCD,
∴∠APC=∠APE-∠EPC=∠PCD-∠PAB.
23(1)、∵AB∥CD(已知)
∴∠BOD=∠B=40°(两直线平行,内错角相等)
∴∠P=∠BOD﹣∠D=40°﹣15°=25°(等式的性质)
(2)、∠BPD=∠B+∠D.理由如下:
过点P作PE∥AB
∵AB∥CD,PE∥AB(已知)
∴AB∥PE∥CD(平行于同一直线的两条直线平行)
∴∠1=∠B,∠2=∠D(两直线平行,内错角相等)
∴∠BPD=∠1+∠2=∠B+∠D(等量代换)
(3)、过点P作GP∥AB交CD于E
过点P作PF∥CD
∵
PE∥AB
∴∠BMD=∠GED=∠GPF=40°,
∠B=∠BPG(两直线平行,内错角相等)
∵
PF∥CD
∴∠D=∠DPF(两直线平行,内错角相等)
∴∠B+∠D=∠BPG+∠DPF(等量代换)
即∠B+∠D
=∠BPD-∠GPF=∠BPD-∠BMD=90°-
40°=50°
第五章
相交线与平行线
5.3.1
平行线的性质
课后练习2
一、选择题
1.如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为(
)
A.20°
B.25°
C.35°
D.50°
2.如图,直线、相交于点,.若,则等于(
)
A.70°
B.110°
C.90°
D.120°
3.如图,直线,直线与,分别相交于,两点,过点作直线的垂线交直线于点,若,则的度数为(
)
A.
B.
C.
D.
4.如图,直线与直线相交,已知,则的度数为(
)
A.
B.
C.
D.
5.如图,若,则图中与互补的角有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于( )
A.70°
B.80°
C.90°
D.100°
7.如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )
A.70°
B.45°
C.110°
D.135°
8.如图,已知AB∥CD,BE和DF分别平分∠ABF和∠CDE,2∠E-∠F=48°,则∠CDE的度数为(
).
A.16°
B.32°
C.48°
D.64°
9.如图,直线,点在上,点、点在上,的角平分线交于点,过点作于点,已知,则的度数为(
)
A.26?
B.32?
C.36?
D.42?
10.如图,BD是△ABC的角平分线,DE∥BC,DE交AB于E,若AB=BC,则下列结论中错误的是(
)
A.BD⊥AC
B.∠A=∠EDA
C.2AD=BC
D.BE=ED
二、填空题
11.如图,,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为_____度.
12.如图,在甲,乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东,若同时开工,则在乙地公路按南偏西___度的走向施工,才能使公路准确接通.
13.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为__.
14.如果的两边分别平行于的两边,且比的2倍少,则________.
15.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为_______.
三、解答题
16.如图,,分别表示两面镜面,一束光线照射到镜面上,反射光线为,此时;光线经过镜面反射后的反射光线为,此时,且.求证∶.
17.如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据)
18.如图,AECF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由.
19.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠ABN的度数是_____,∠CBD的度数是_______;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是多少?
20.如图,∠1=∠2,∠3=∠4,∠5=∠6,求证:AD∥BC
21.已知:如图(1),直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.(1)求∠EKF的度数.(计算过程不准用三角形内角和)(2)如图(2),∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)
22.如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC+∠PAB+∠PCD=
;
(2)图②中,
;
(3)图③中,写出∠APC与∠PAB,∠PCD的三者数量关系,并说明理由
23.(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD
°.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
【参考答案】
1.A
2.B
3.D
4.B
5.D
6.B
7.C
8.B
9.A
10.C
11.
12.55
13.132°
14.或
15.或
16.解:证明:∵,
∴,
又∵,
∴,
又∵,,
∴,
∴.
17.证明:∵∠DGA=∠EGC(对顶角相等)
又∵∠DGA=∠FHC(已知)
∴∠EGC=∠FHC(等量代换)
∴AE∥BF
(同位角相等,两直线平行)
∴∠A=∠FBC
(两直线平行,同位角相等)
又∵∠A=∠F(已知)
∴∠F=∠FBC
(等量代换)
∴DF∥AC
(内错角相等,两直线平行).
18.解:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,
∴∠A+∠ADC=180°,
又∵∠A=∠C,
∴∠C+∠ADC=180°,
∴BC∥AD.
19.(1)∵AM//BN,∠A=64°,
∴∠ABN=180°﹣∠A=116°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=116°,
∴∠CBD=∠CBP+∠DBP=58°;
故答案为:116°;58°;
(2)不变,∠APB=2∠ADB,
∵AM//BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AM//BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN
∴∠ABC=∠DBN,
由(1)∠ABN=116°,
∴∠CBD=58°,
∴∠ABC+∠DBN=58°,
∴∠ABC=29°.
20.∵∠5=∠6
∴AB∥CD
∴∠4+∠BAE=180°
∴∠4+∠2+∠5=180°
∵∠3=∠4,∠1=∠2
∴∠3+∠1+∠5=180°
∴∠5+∠ABC=180°
∴AD∥BC
21.(1)过K作KG∥AB,可得KG∥CD,如图所示:
∴∠BEK=∠EKG,∠GKF=∠KFD,
∵EK、FK分别为∠BEF与∠EFD的平分线,
∴∠BEK=∠FEK,∠EFK=∠DFK,
∵AB∥CD,
∴∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠DFK)=180°,
∴∠BEK+∠DFK=90°,则∠EKF=∠EKG+∠GKF=90°;
(2)∠K=2∠K1,理由为:
∵∠BEK、∠DFK的平分线相交于点K1,
∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,
∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,
∴∠BEK+∠KFD=90°,即∠KEK1+∠KFK1=45°,
∴∠K1=180°-(∠KEF+∠EFK)-(∠KEK1+∠KFK1)=45°,则∠K=2∠K1;
(3)归纳总结得:∠Kn+1=
×90°。
点睛:解本题主要运用了平行线的性质,角平分线定义,属于探究型试题,熟练掌握平行线的性质是解本题的关键。
22.三个图形中过P作PE与AB平行,由AB与CD平行,利用平行于同一条直线的两直线平行得到PE与CD平行,利用平行线的性质判断即可得到结果.
试题解析:(1)过P作PE∥AB,如图①
∵AB∥CD,
∴PE∥CD,
∴∠A+∠APE=180°,∠EPC+∠C=180°,
∴∠APC+∠PAB+∠PCD=∠A+∠APE+∠EPC+∠C=360°;
(2)过P作PE∥AB,如图②
∵AB∥CD,
∴PE∥CD,
∴∠A=∠APE,∠EPC=∠C,
∴∠APC=∠APE+∠EPC=∠PAB+∠PCD;
(3)∠APC=∠PCD-∠PAB,
理由为:过P作PE∥AB,如图③
∵AB∥CD,
∴PE∥CD,
∴∠PAB+∠APE=180°,∠EPC+∠PCD=180°,
即∠APE=180°-∠PAB,∠EPC=180°-∠PCD,
∴∠APC=∠APE-∠EPC=∠PCD-∠PAB.
23(1)、∵AB∥CD(已知)
∴∠BOD=∠B=40°(两直线平行,内错角相等)
∴∠P=∠BOD﹣∠D=40°﹣15°=25°(等式的性质)
(2)、∠BPD=∠B+∠D.理由如下:
过点P作PE∥AB
∵AB∥CD,PE∥AB(已知)
∴AB∥PE∥CD(平行于同一直线的两条直线平行)
∴∠1=∠B,∠2=∠D(两直线平行,内错角相等)
∴∠BPD=∠1+∠2=∠B+∠D(等量代换)
(3)、过点P作GP∥AB交CD于E
过点P作PF∥CD
∵
PE∥AB
∴∠BMD=∠GED=∠GPF=40°,
∠B=∠BPG(两直线平行,内错角相等)
∵
PF∥CD
∴∠D=∠DPF(两直线平行,内错角相等)
∴∠B+∠D=∠BPG+∠DPF(等量代换)
即∠B+∠D
=∠BPD-∠GPF=∠BPD-∠BMD=90°-
40°=50°
