冀教版数学八年级上册期末水平测试题(1)及答案
文档属性
| 名称 | 冀教版数学八年级上册期末水平测试题(1)及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-08 10:14:03 | ||
图片预览

文档简介
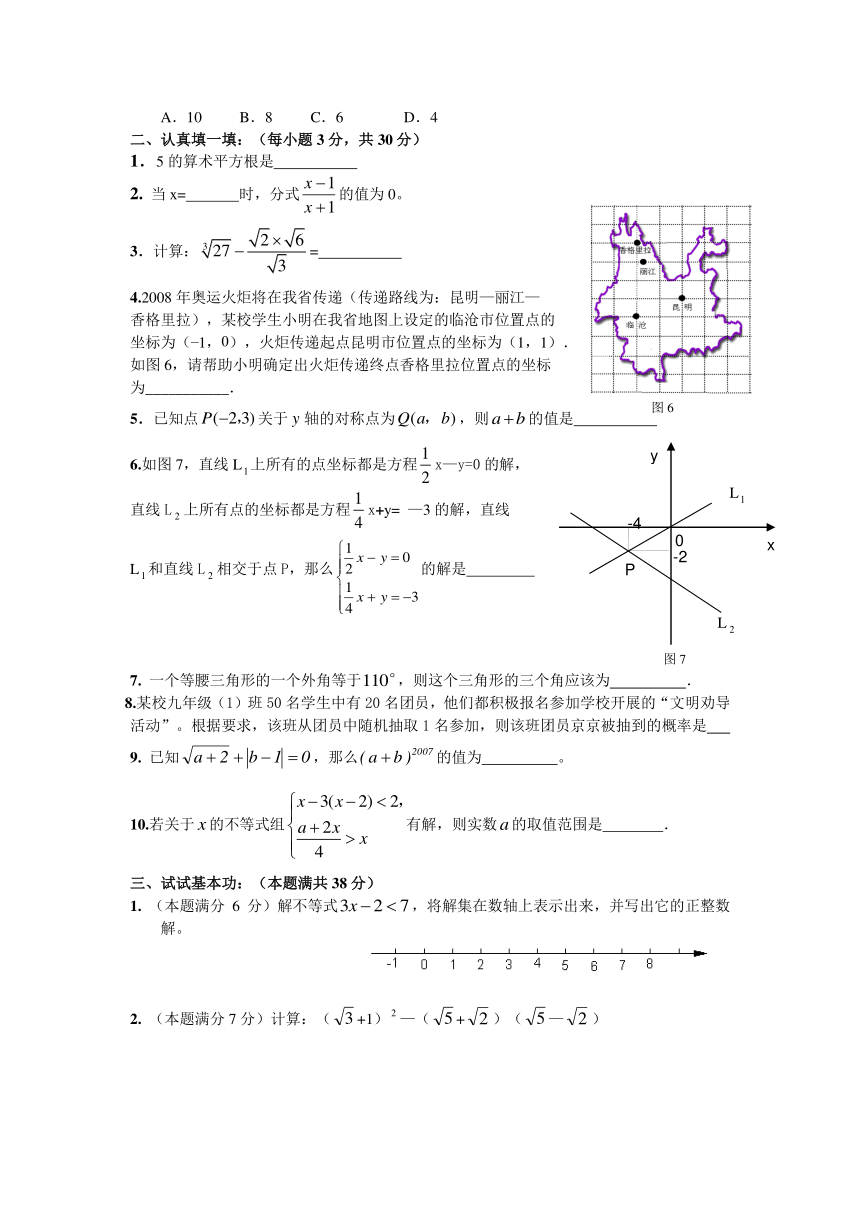
八年级上册期末考试数学水平测试(1)
(本卷满分 120分)
一、精心选一选:(每小题3分,共30分)
1.9的平方根是( )。
A、3 B、-3 C、±3 D、81
2.如图1,下列各点在阴影区域内的是 ( )
A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2)
3.计算: 的结果是( )
A. B. C. D.
4. 若不等式组的解集在数轴上表示如图2,则这个不等式组是( )
A. B. C. D.
5.下列事件中,是必然事件的是( )
A.购买一张彩票中奖一百万。B.打开电视机,任选一个频道,正在播新闻。
C.在地球上,上抛出去的篮球会下落。
D.掷两枚质地均匀的正方形骰子,点数之和一定大于6。
6.如图3,是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是( )。
7.下列各数中,,0.101001000100001……(每两个1之间多一个0),—,2.8888………,无理数有( )个。
A.1 B.2 C.3 D.4
8.如图4,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
A. cm B.4cm C. cm D. 3cm
9.某次环保知识竞赛试卷有20道题。平分办法是答对一题记5 分,答错一题扣2分,不答记0分。小明有3道题没答,但成绩超过了60分。
小明最多答对了( )道题。
A.14 B.15 C.16 D.17
10.如图5,ABC是等边三角形,BD是中线,DEBC于E。
若EC=2,则BE=( )
A.10 B.8 C.6 D.4
二、认真填一填:(每小题3分,共30分)
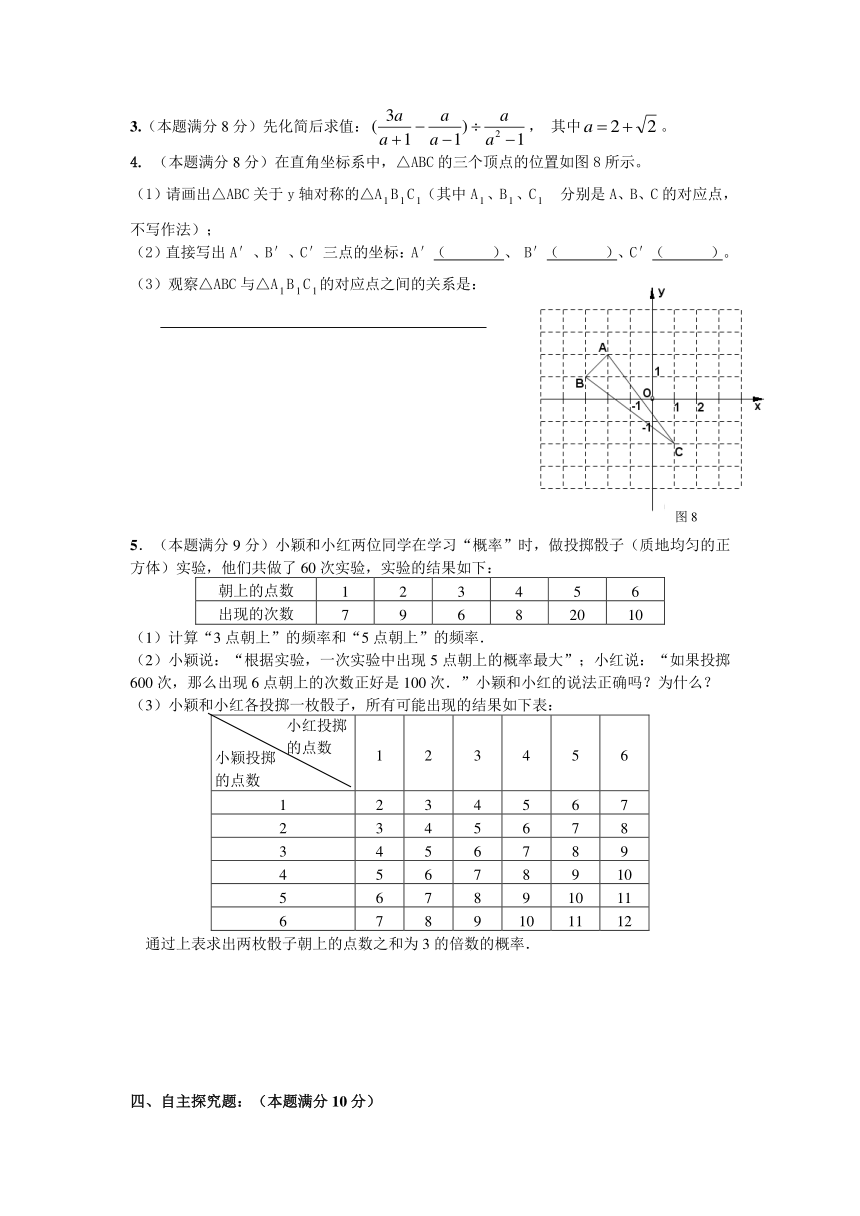
1.5的算术平方根是
2. 当x= 时,分式的值为0。
3.计算:=
4.2008年奥运火炬将在我省传递(传递路线为:昆明—丽江—
香格里拉),某校学生小明在我省地图上设定的临沧市位置点的
坐标为(–1,0),火炬传递起点昆明市位置点的坐标为(1,1).
如图6,请帮助小明确定出火炬传递终点香格里拉位置点的坐标
为___________.
5.已知点关于轴的对称点为,则的值是
6.如图7,直线L上所有的点坐标都是方程x—y=0的解,
直线L上所有点的坐标都是方程x+y= —3的解,直线
L和直线L相交于点P,那么的解是
7. 一个等腰三角形的一个外角等于,则这个三角形的三个角应该为 .
8.某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”。根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是
9. 已知,那么的值为 。
10.若关于的不等式组有解,则实数的取值范围是 .
三、试试基本功:(本题满共38分)
1. (本题满分6分)解不等式,将解集在数轴上表示出来,并写出它的正整数解。
2. (本题满分7分)计算:(+1)—(+)(—)
3.(本题满分8分)先化简后求值:, 其中。
4. (本题满分8分)在直角坐标系中,△ABC的三个顶点的位置如图8所示。
(1)请画出△ABC关于y轴对称的△ABC(其中A、B、C 分别是A、B、C的对应点,不写作法);
(2)直接写出A′、B′、C′三点的坐标:A′( )、 B′( )、C′( )。
(3)观察△ABC与△ABC的对应点之间的关系是:
5.(本题满分9分)小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,所有可能出现的结果如下表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
通过上表求出两枚骰子朝上的点数之和为3的倍数的概率.
四、自主探究题:(本题满分10分)
如图9,已知ABC中 AB=AC,A=36°,使点A、B重合对折,折痕为MD,连接BD。若BCD的周长为5,BC=2。
(1)图中除ABC外还有哪些等腰三角形,
并选其中一个三角形说明理由。
(2)求ABC的周长。
(3)求折痕MD的长。
五、生活中的数学:(本题满分12分)
7.2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
参考答案
一、精心选一选:(每小题3分,共30分)
1.C 2.A 3.B 4.C 5.C 6.B 7.C 8.A 9.D 10.C
二、认真填一填:(每小题3分,共30分)
1. ; 2. 1 ;3. 1 ;4.(-1,4) ; 5. 5 ; 6. ;
7. 55°、55°、70°或70°、70°、40°; 8. ; 9.-1 ;10. >4 ;
三、试试基本功:(本题满共38分)
1. 解:移向得3x<9
x<3
不等式的解集在数轴表示为:
2.解:原式=3+2+1—(5—2)
=4+2—3
=1+ 2
3. 解:原式=
=
=
当时,原式=
4. 解:(1)如图8;
(2),,)
(3)对应点的横坐标互为相反数,纵坐标不变。
5.解:(1)“3点朝上”出现的频率是
“5点朝上”出现的频率是
(2)小颖的说法是错误的.这是因为,“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的频率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近.小红的判断是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
(3)
四、自主探究题:(本题满分10分)
解:(1)ADB、BDC是等腰三角形。
因为A与=ABD重合
所以A=ABD
所以BD=AD,即ADB是等腰三角形。
(2)因为BD=AD,BCD的周长为5
所以AC+BC=5ABC的周长
所以AC=5—BC=5—2=3
所以ABC的周长为AC+BC+AB=5+3=8
(3)因为AC=3,D为AB中点,
所以AM=,MDAB
因为AB=AC,A=36°
所以ABC=ACB=72°
又因为A=ABD=36°
所以DBC=36°,BDC=72°
所以BD=BC=AD=2
由勾股定理得,MD====
五、生活中的数学:(本题满分12分)
解:设搭配种造型个,则种造型为个,
依题意,得:
解这个不等式组,得:,
是整数,可取,
可设计三种搭配方案:
①种园艺造型个 种园艺造型个
②种园艺造型个 种园艺造型个
③种园艺造型个 种园艺造型个.
(2)方法一:由于种造型的造价成本高于种造型成本.所以种造型越少,成本越低,故应选择方案③,成本最低,最低成本为:(元)
方法二:方案①需成本:(元)
方案②需成本:(元)
方案③需成本:元
应选择方案③,成本最低,最低成本为元.
2
0
○
-1
·
图2
图3
A
B
C
D
图4
图4
B
A
C
D
E
图5
图6
A
P
x
y
0
图7
-2
-4
L
L
图8
小红投掷
的点数
小颖投掷
的点数
A
M
D
C
B
图9
C
A
B
图8
(本卷满分 120分)
一、精心选一选:(每小题3分,共30分)
1.9的平方根是( )。
A、3 B、-3 C、±3 D、81
2.如图1,下列各点在阴影区域内的是 ( )
A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2)
3.计算: 的结果是( )
A. B. C. D.
4. 若不等式组的解集在数轴上表示如图2,则这个不等式组是( )
A. B. C. D.
5.下列事件中,是必然事件的是( )
A.购买一张彩票中奖一百万。B.打开电视机,任选一个频道,正在播新闻。
C.在地球上,上抛出去的篮球会下落。
D.掷两枚质地均匀的正方形骰子,点数之和一定大于6。
6.如图3,是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是( )。
7.下列各数中,,0.101001000100001……(每两个1之间多一个0),—,2.8888………,无理数有( )个。
A.1 B.2 C.3 D.4
8.如图4,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
A. cm B.4cm C. cm D. 3cm
9.某次环保知识竞赛试卷有20道题。平分办法是答对一题记5 分,答错一题扣2分,不答记0分。小明有3道题没答,但成绩超过了60分。
小明最多答对了( )道题。
A.14 B.15 C.16 D.17
10.如图5,ABC是等边三角形,BD是中线,DEBC于E。
若EC=2,则BE=( )
A.10 B.8 C.6 D.4
二、认真填一填:(每小题3分,共30分)
1.5的算术平方根是
2. 当x= 时,分式的值为0。
3.计算:=
4.2008年奥运火炬将在我省传递(传递路线为:昆明—丽江—
香格里拉),某校学生小明在我省地图上设定的临沧市位置点的
坐标为(–1,0),火炬传递起点昆明市位置点的坐标为(1,1).
如图6,请帮助小明确定出火炬传递终点香格里拉位置点的坐标
为___________.
5.已知点关于轴的对称点为,则的值是
6.如图7,直线L上所有的点坐标都是方程x—y=0的解,
直线L上所有点的坐标都是方程x+y= —3的解,直线
L和直线L相交于点P,那么的解是
7. 一个等腰三角形的一个外角等于,则这个三角形的三个角应该为 .
8.某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”。根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是
9. 已知,那么的值为 。
10.若关于的不等式组有解,则实数的取值范围是 .
三、试试基本功:(本题满共38分)
1. (本题满分6分)解不等式,将解集在数轴上表示出来,并写出它的正整数解。
2. (本题满分7分)计算:(+1)—(+)(—)
3.(本题满分8分)先化简后求值:, 其中。
4. (本题满分8分)在直角坐标系中,△ABC的三个顶点的位置如图8所示。
(1)请画出△ABC关于y轴对称的△ABC(其中A、B、C 分别是A、B、C的对应点,不写作法);
(2)直接写出A′、B′、C′三点的坐标:A′( )、 B′( )、C′( )。
(3)观察△ABC与△ABC的对应点之间的关系是:
5.(本题满分9分)小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,所有可能出现的结果如下表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
通过上表求出两枚骰子朝上的点数之和为3的倍数的概率.
四、自主探究题:(本题满分10分)
如图9,已知ABC中 AB=AC,A=36°,使点A、B重合对折,折痕为MD,连接BD。若BCD的周长为5,BC=2。
(1)图中除ABC外还有哪些等腰三角形,
并选其中一个三角形说明理由。
(2)求ABC的周长。
(3)求折痕MD的长。
五、生活中的数学:(本题满分12分)
7.2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
参考答案
一、精心选一选:(每小题3分,共30分)
1.C 2.A 3.B 4.C 5.C 6.B 7.C 8.A 9.D 10.C
二、认真填一填:(每小题3分,共30分)
1. ; 2. 1 ;3. 1 ;4.(-1,4) ; 5. 5 ; 6. ;
7. 55°、55°、70°或70°、70°、40°; 8. ; 9.-1 ;10. >4 ;
三、试试基本功:(本题满共38分)
1. 解:移向得3x<9
x<3
不等式的解集在数轴表示为:
2.解:原式=3+2+1—(5—2)
=4+2—3
=1+ 2
3. 解:原式=
=
=
当时,原式=
4. 解:(1)如图8;
(2),,)
(3)对应点的横坐标互为相反数,纵坐标不变。
5.解:(1)“3点朝上”出现的频率是
“5点朝上”出现的频率是
(2)小颖的说法是错误的.这是因为,“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的频率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近.小红的判断是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
(3)
四、自主探究题:(本题满分10分)
解:(1)ADB、BDC是等腰三角形。
因为A与=ABD重合
所以A=ABD
所以BD=AD,即ADB是等腰三角形。
(2)因为BD=AD,BCD的周长为5
所以AC+BC=5ABC的周长
所以AC=5—BC=5—2=3
所以ABC的周长为AC+BC+AB=5+3=8
(3)因为AC=3,D为AB中点,
所以AM=,MDAB
因为AB=AC,A=36°
所以ABC=ACB=72°
又因为A=ABD=36°
所以DBC=36°,BDC=72°
所以BD=BC=AD=2
由勾股定理得,MD====
五、生活中的数学:(本题满分12分)
解:设搭配种造型个,则种造型为个,
依题意,得:
解这个不等式组,得:,
是整数,可取,
可设计三种搭配方案:
①种园艺造型个 种园艺造型个
②种园艺造型个 种园艺造型个
③种园艺造型个 种园艺造型个.
(2)方法一:由于种造型的造价成本高于种造型成本.所以种造型越少,成本越低,故应选择方案③,成本最低,最低成本为:(元)
方法二:方案①需成本:(元)
方案②需成本:(元)
方案③需成本:元
应选择方案③,成本最低,最低成本为元.
2
0
○
-1
·
图2
图3
A
B
C
D
图4
图4
B
A
C
D
E
图5
图6
A
P
x
y
0
图7
-2
-4
L
L
图8
小红投掷
的点数
小颖投掷
的点数
A
M
D
C
B
图9
C
A
B
图8
同课章节目录
