冀教版数学八年级上册期末水平测试题(2)及答案
文档属性
| 名称 | 冀教版数学八年级上册期末水平测试题(2)及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-08 10:13:21 | ||
图片预览


文档简介
八年级上册数学水平测试(2)
一、认认真真选,沉着应战!(每小题3分;共30分)
1.已知,下列四个不等式中,不正确的是( )
A. B. C. D.
2. 关于x的不等式组只有4个整数解,则a的取值范围是( )
A. -5≤a≤- B. -5≤a<- C. -5<a≤- D. -5<a<-
3.设,,用含的式子表示,则下列表示正确的是( )
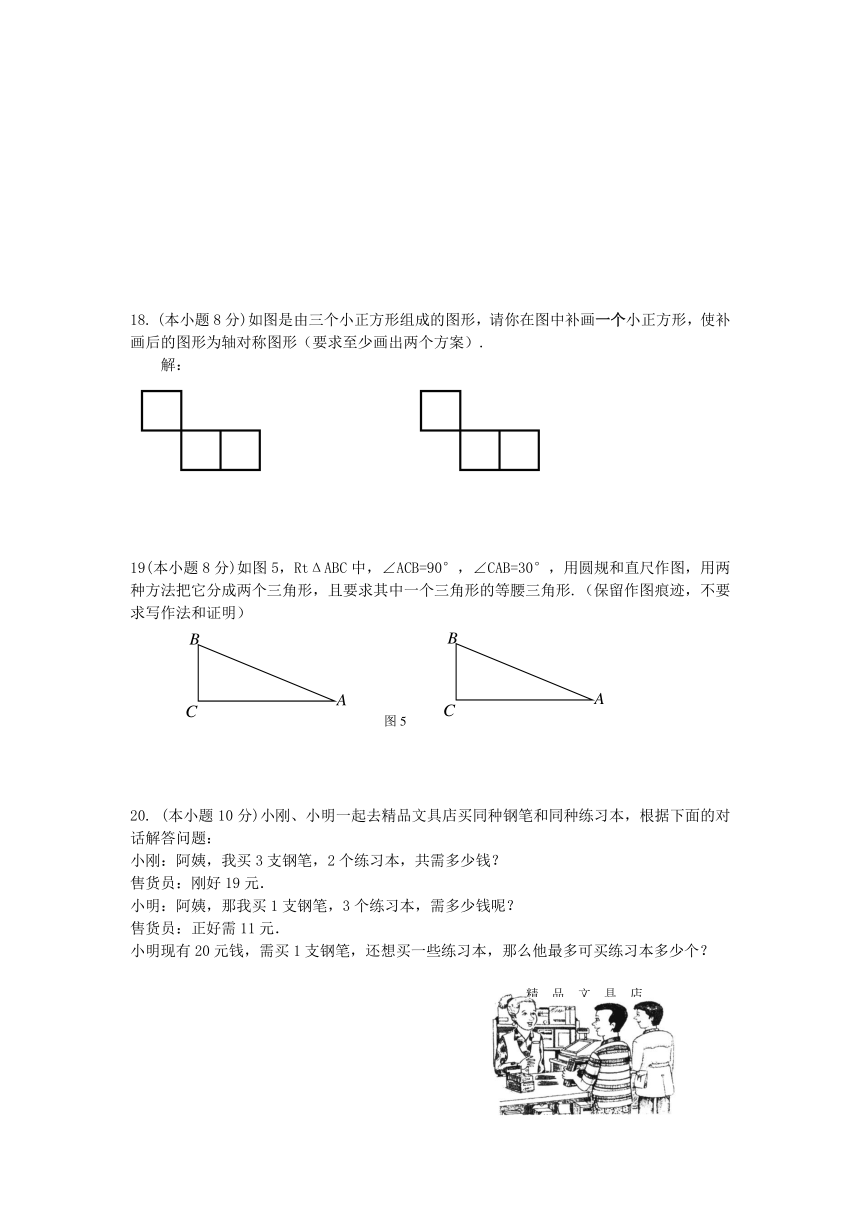
A. B. C. D.
4.已知两个分式:,,其中,则A与B 的关系是( )
A.相等 B.互为倒数 C.互为相反数 D.A大于B
5.已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A的对应点A'的坐标为( ).
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
6.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④若A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如果代数式有意义,那么,直角坐标系中点P(m,n)的位置在( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图,B在A的北偏西α方向的6m处,C在A的北偏东β
方向的8m处,并且,那么B、C两点相距( )
A.6m B.8m C.10m D.12m
9.某商店的老板销售一种商品,他要以不低于进价20%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价( ),商店老板才能出售.
A.80元 B.100元 C.120元 D.160元
10.从分别标有2,3,4,5,6,7的卡片中任意抽取一张,考查下列事件:①取到2的倍数;②取到质数;③取到奇数;④取到3的倍数,其中发生的可能性最大的是( )
A.① B.② C. ③ D.④
二、仔仔细细填,记录自信!(每小题3分,共15分)
11.若不等式的解集是,则不等式的解集是 .
12.若使分式的值为0,则的取值为
13.在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,
折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于
点D和点E(如图),折痕DE的长为 .
14.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体
无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
15.如图,在四个正方形拼接成的图形中,以、、、…、
这十个点中任意三点为顶点,共能组成________个等腰直角三角形.
你愿意把得到上述结论的探究方法与他人交流吗
若愿意,请在下方简要写出你的探究过程
(结论正确且所写的过程敏捷合理可另加2分):________________________________________________________
___________________________________________________________________________________________________________________________________________________.
三、平心静气做,展示智慧!(本大题共42分)
16. (本小题7分)先化简再求值:,
其中.
17. (本小题8分)如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
⑴写出下一步“马”可能到达的点的坐标
;
⑵按横坐标从小到大顺次连接⑴中的所有点,得到的
图形是否为轴对称图形答:________
18. (本小题8分)如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形(要求至少画出两个方案).
解:
19(本小题8分)如图5,RtΔABC中,∠ACB=90°,∠CAB=30°,用圆规和直尺作图,用两种方法把它分成两个三角形,且要求其中一个三角形的等腰三角形.(保留作图痕迹,不要求写作法和证明)
20. (本小题10分)小刚、小明一起去精品文具店买同种钢笔和同种练习本,根据下面的对话解答问题:
小刚:阿姨,我买3支钢笔,2个练习本,共需多少钱?
售货员:刚好19元.
小明:阿姨,那我买1支钢笔,3个练习本,需多少钱呢?
售货员:正好需11元.
小明现有20元钱,需买1支钢笔,还想买一些练习本,那么他最多可买练习本多少个?
21. (本小题10分)王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,试求出现向上点数之和为3的倍数的概率.
四、发散思维,游刃有余(本大题共24分)
22. (本小题12分)我们把分子为1的分数叫做单位分数. 如,,…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如=,=,=,…
(1)根据对上述式子的观察,你会发现=. 请写出□,○所表示的数;
(2)进一步思考,单位分数(n是不小于2的正整数)=,请写出△,☆所表示的式,并加以验证.
23. (本题12分)△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与的关系,并证明你的结论.
参考答案
一、1.B 2.C 3.A 4. C 5.D 6.B 7.C 8. C 9.C 10.B
二、
11.
12.
13.1
14. 5
15. 30 设小正方形的边长为1,则等腰直角三角形有以下三种情形: (1)直角边长为1的等腰直角三角形有4×4+2=18个;(2)直角边长为的等腰直角三角形有2×5=10个;(3)直角边长为2的等腰直角三角形有2个.所以等腰直角三角形共有18+10+2=30个.
三、
16.解:原式
当 时
原式
17.(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0) (2)是轴对称图形
18. 参考图如下图:
19.作法一:作AB边上的中线;
作法二:作∠CBA的平分线;
作法三:在CA上取一点D,使CD=CB.
20.解:设买一支钢笔要元,买一个练习本要元
依题意:
解之得
设买的练习本为个
则
得.因为为非负整数,所以的最大值为
答:小明最多可买7个练习本.
21. (1)出现向上点数为3的频率为,出现向上点数为5的频率为
(2)都错 (3)概率P=
四、
22.(1)□表示的数为6,○表示的数为30;
(2)△表示的式为,☆表示的式为.
∵
23.若△ABC是锐角三角形,则有
若△ABC是钝角三角形,为钝角,则有.
当△ABC是锐角三角形时,
证明:过点A作ADBC,垂足为D,设CD为,则有BD=
根据勾股定理,得 即.
∴
∵, ∴. ∴.
当△ABC是钝角三角形时,
证明:过B作BDAC,交AC的延长线于D.
设CD为,则有 根据勾股定理,得.
即.
∵, ∴, ∴.
图5
精 品 文 具 店
□
○
☆
△
一、认认真真选,沉着应战!(每小题3分;共30分)
1.已知,下列四个不等式中,不正确的是( )
A. B. C. D.
2. 关于x的不等式组只有4个整数解,则a的取值范围是( )
A. -5≤a≤- B. -5≤a<- C. -5<a≤- D. -5<a<-
3.设,,用含的式子表示,则下列表示正确的是( )
A. B. C. D.
4.已知两个分式:,,其中,则A与B 的关系是( )
A.相等 B.互为倒数 C.互为相反数 D.A大于B
5.已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A的对应点A'的坐标为( ).
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
6.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④若A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如果代数式有意义,那么,直角坐标系中点P(m,n)的位置在( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图,B在A的北偏西α方向的6m处,C在A的北偏东β
方向的8m处,并且,那么B、C两点相距( )
A.6m B.8m C.10m D.12m
9.某商店的老板销售一种商品,他要以不低于进价20%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价( ),商店老板才能出售.
A.80元 B.100元 C.120元 D.160元
10.从分别标有2,3,4,5,6,7的卡片中任意抽取一张,考查下列事件:①取到2的倍数;②取到质数;③取到奇数;④取到3的倍数,其中发生的可能性最大的是( )
A.① B.② C. ③ D.④
二、仔仔细细填,记录自信!(每小题3分,共15分)
11.若不等式的解集是,则不等式的解集是 .
12.若使分式的值为0,则的取值为
13.在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,
折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于
点D和点E(如图),折痕DE的长为 .
14.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体
无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
15.如图,在四个正方形拼接成的图形中,以、、、…、
这十个点中任意三点为顶点,共能组成________个等腰直角三角形.
你愿意把得到上述结论的探究方法与他人交流吗
若愿意,请在下方简要写出你的探究过程
(结论正确且所写的过程敏捷合理可另加2分):________________________________________________________
___________________________________________________________________________________________________________________________________________________.
三、平心静气做,展示智慧!(本大题共42分)
16. (本小题7分)先化简再求值:,
其中.
17. (本小题8分)如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
⑴写出下一步“马”可能到达的点的坐标
;
⑵按横坐标从小到大顺次连接⑴中的所有点,得到的
图形是否为轴对称图形答:________
18. (本小题8分)如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形(要求至少画出两个方案).
解:
19(本小题8分)如图5,RtΔABC中,∠ACB=90°,∠CAB=30°,用圆规和直尺作图,用两种方法把它分成两个三角形,且要求其中一个三角形的等腰三角形.(保留作图痕迹,不要求写作法和证明)
20. (本小题10分)小刚、小明一起去精品文具店买同种钢笔和同种练习本,根据下面的对话解答问题:
小刚:阿姨,我买3支钢笔,2个练习本,共需多少钱?
售货员:刚好19元.
小明:阿姨,那我买1支钢笔,3个练习本,需多少钱呢?
售货员:正好需11元.
小明现有20元钱,需买1支钢笔,还想买一些练习本,那么他最多可买练习本多少个?
21. (本小题10分)王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,试求出现向上点数之和为3的倍数的概率.
四、发散思维,游刃有余(本大题共24分)
22. (本小题12分)我们把分子为1的分数叫做单位分数. 如,,…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如=,=,=,…
(1)根据对上述式子的观察,你会发现=. 请写出□,○所表示的数;
(2)进一步思考,单位分数(n是不小于2的正整数)=,请写出△,☆所表示的式,并加以验证.
23. (本题12分)△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与的关系,并证明你的结论.
参考答案
一、1.B 2.C 3.A 4. C 5.D 6.B 7.C 8. C 9.C 10.B
二、
11.
12.
13.1
14. 5
15. 30 设小正方形的边长为1,则等腰直角三角形有以下三种情形: (1)直角边长为1的等腰直角三角形有4×4+2=18个;(2)直角边长为的等腰直角三角形有2×5=10个;(3)直角边长为2的等腰直角三角形有2个.所以等腰直角三角形共有18+10+2=30个.
三、
16.解:原式
当 时
原式
17.(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0) (2)是轴对称图形
18. 参考图如下图:
19.作法一:作AB边上的中线;
作法二:作∠CBA的平分线;
作法三:在CA上取一点D,使CD=CB.
20.解:设买一支钢笔要元,买一个练习本要元
依题意:
解之得
设买的练习本为个
则
得.因为为非负整数,所以的最大值为
答:小明最多可买7个练习本.
21. (1)出现向上点数为3的频率为,出现向上点数为5的频率为
(2)都错 (3)概率P=
四、
22.(1)□表示的数为6,○表示的数为30;
(2)△表示的式为,☆表示的式为.
∵
23.若△ABC是锐角三角形,则有
若△ABC是钝角三角形,为钝角,则有.
当△ABC是锐角三角形时,
证明:过点A作ADBC,垂足为D,设CD为,则有BD=
根据勾股定理,得 即.
∴
∵, ∴. ∴.
当△ABC是钝角三角形时,
证明:过B作BDAC,交AC的延长线于D.
设CD为,则有 根据勾股定理,得.
即.
∵, ∴, ∴.
图5
精 品 文 具 店
□
○
☆
△
同课章节目录
