青岛版数学九年级上4.6圆与圆的位置关系课件
文档属性
| 名称 | 青岛版数学九年级上4.6圆与圆的位置关系课件 |  | |
| 格式 | rar | ||
| 文件大小 | 275.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-08 10:42:29 | ||
图片预览




文档简介
(共32张PPT)
4.6圆与圆的位置关系
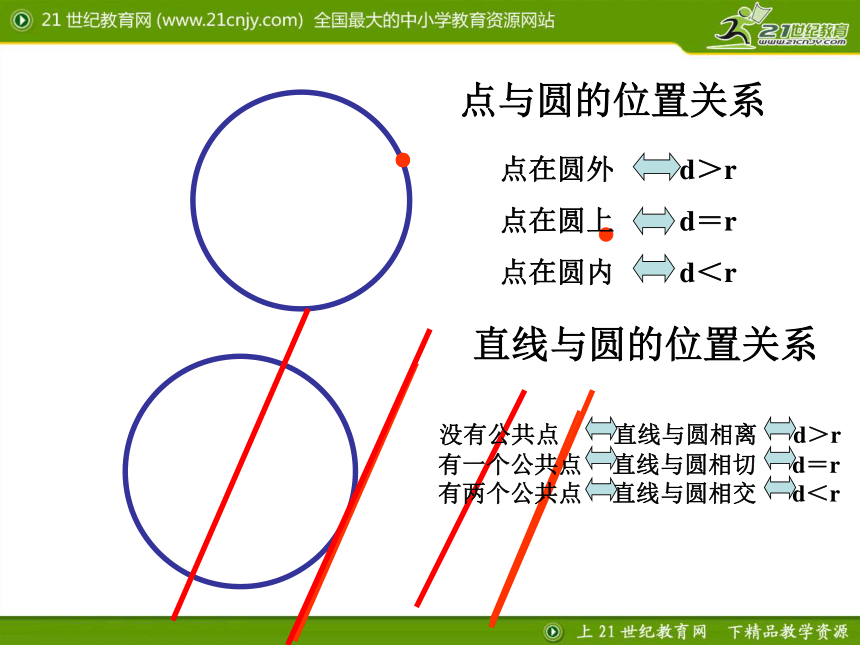
点与圆的位置关系
直线与圆的位置关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
没有公共点 直线与圆相离 d>r
有一个公共点 直线与圆相切 d=r
有两个公共点 直线与圆相交 d<r
初步感知
探究一
圆与圆有哪几种位置关系?
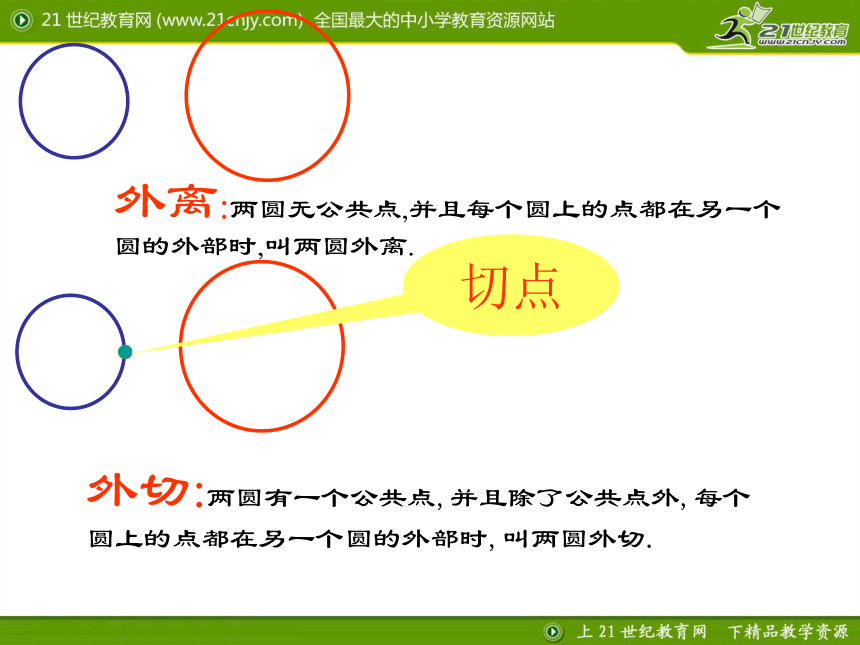
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
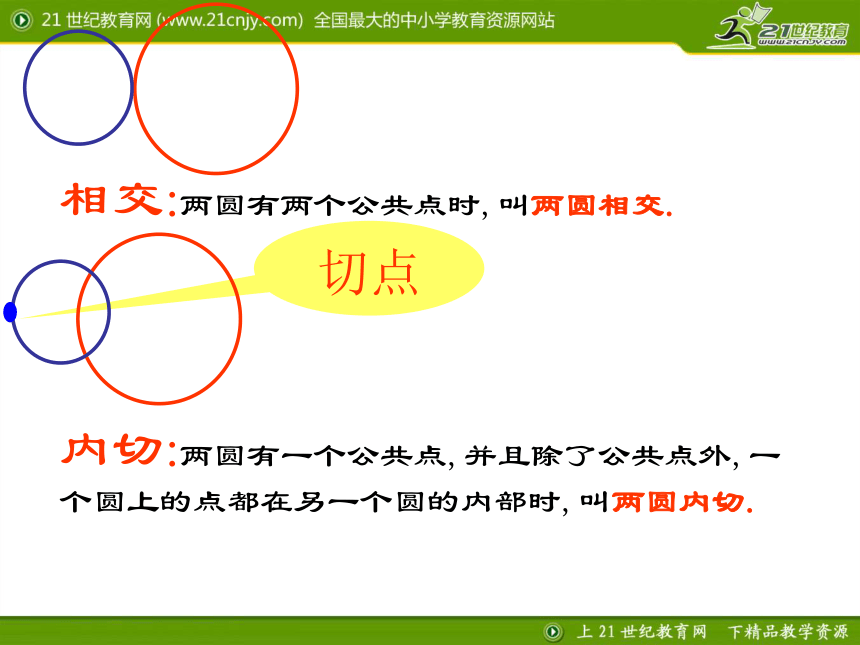
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
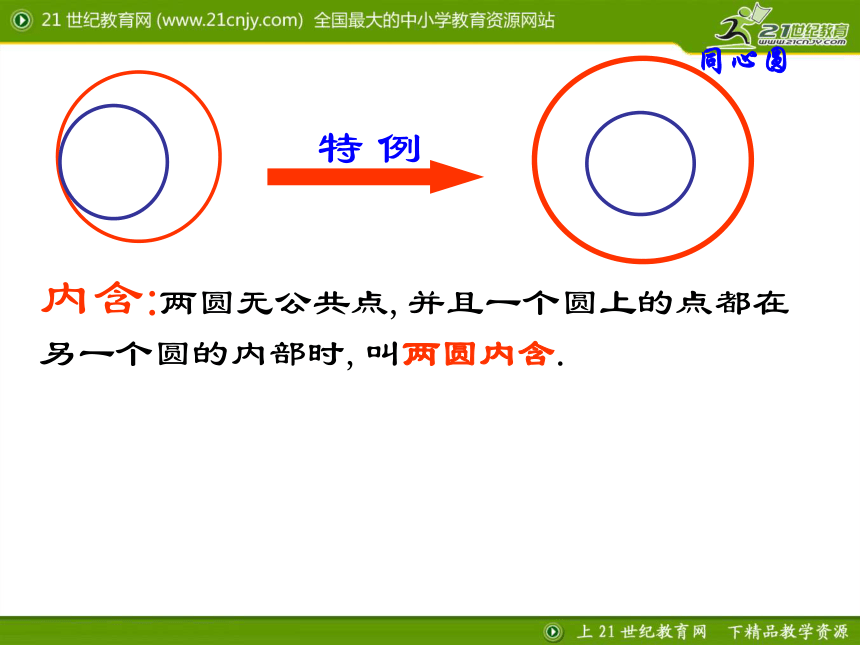
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
同心圆
圆
和
圆
的
位
置
关
系
外 离
内切
相交
外切
内含
没有公共点
相 离
一个公共点
相切
两个公共点
相 交
圆与圆的位置关系
圆心距:两圆圆心之间的距离
1.⊙A和⊙B外离
d>r1+r2
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
2.⊙A和⊙B外切
d=r1+r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
r1-r23.⊙A和⊙B相交
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
4.⊙A和⊙B内切
d=r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
5.⊙A和⊙B内含
dA
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
两圆的半径,圆心距在它们不同位置时的数量关系:
1.⊙A和⊙B外离
d>r1+r2
2.⊙A和⊙B外切
d=r1+r2
3.⊙A和⊙B相交
r1-r24.⊙A和⊙B内切
5.⊙A和⊙B内含
d=r1-r2
d2)⊙01和⊙02 的半径分别为3cm 和 5 cm ,
当0102= 8cm时,两圆的位置关是 .
当0102= 2cm时,两圆的位置关是 .
当0102= 10cm时,两圆的位置关是 .
1、看谁答得快
1)两圆有两个交点,则两圆的位置关系是 .
两圆没有交点,则两圆的位置关系是 .
两圆只有一个交点,则两圆的位置关系是 .
3) 当两圆外切, 0102= 10,r1=4时,r2= .
当两圆内切, 0102= 2,r1=5时,r2 = .
学以致用
如图,⊙O与⊙P分别相切于点A和点B, 则此图是对称图行吗,如果是,画出它的对称轴。
A
B
P
O
动脑筋
相切两圆的性质
1、通过两圆圆心的直线叫做连心线。
2、如果两个圆相切,那么切点一定
在连心线上。
连心线:是指通过两圆圆心的一条直线。
分析:连心线是它的对称轴。两圆相切时,由
于切点是它们唯一的公共点,所以切点一定在对
称轴上。
例1 如图,⊙O的半径为5 cm,点P是⊙O外一点,OP=8 cm.以P点为圆心作⊙P与⊙O相切, 则⊙P的半径是多少
解:(1)设⊙O与⊙P外切于点A,
则 PA=OP-OA
所以PA=3 cm,
(2)设⊙O与⊙P内切于点B,
则 PB=PO+OB
所以PB=13 cm.
A
B
P
O
应 用
例2 已知两圆半径分别为3和4,圆心的坐标分别是(0,3)和(4,0),试判断这两圆的位置关系.
应 用
y
x
练习
1、举出一些能表示两个圆不同位置关系的实例。
2、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,设
(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)外离 (2)外切
(3)相交 (4)内切
(5)内含 (6)同心圆
3.定圆⊙O半径为3cm,动圆⊙P半径为1cm.
当两圆 时,OP为 cm?点P可以在什么样的线上运动?
O
P
外切
内切
当两圆相切时,OP为多少?
动脑筋
两个等圆有那几种位置关系?
(外离.外切.相交.重合)
圆与圆的位置关系(从公共点个数看)
(没有公共点)
(有1个公共点)
(有2个公共点)
相离
外离
内含
特殊情况
同心圆
相切
外切
内切
相交
圆与圆的五种位置关系
相交
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r两圆内切 d = R r 1
两圆内含 0≤ dr) 0
性质
判定
两圆位置关系的性质与判定:
课堂检测
1、已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距0102=7cm,则两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内切
2、已知与外切,它们的半径分别为2和3,则圆心距d的长是( )
A.d=1 B.d=5 C.1<d<5 D.d>5
3、两圆的圆心距为3,两圆的半径分别是方程的两个根,则两圆的位置关系是 ( )
课堂检测
4、如图,⊙O的半径为5cm,点P是⊙O外一点,OP
=8cm,求(1)以P为圆心作⊙P与⊙O外切,圆⊙P
的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆
⊙P的半径是多少?
P
A
B
O
4.6圆与圆的位置关系
点与圆的位置关系
直线与圆的位置关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
没有公共点 直线与圆相离 d>r
有一个公共点 直线与圆相切 d=r
有两个公共点 直线与圆相交 d<r
初步感知
探究一
圆与圆有哪几种位置关系?
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
同心圆
圆
和
圆
的
位
置
关
系
外 离
内切
相交
外切
内含
没有公共点
相 离
一个公共点
相切
两个公共点
相 交
圆与圆的位置关系
圆心距:两圆圆心之间的距离
1.⊙A和⊙B外离
d>r1+r2
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
2.⊙A和⊙B外切
d=r1+r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
4.⊙A和⊙B内切
d=r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
5.⊙A和⊙B内含
d
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
两圆的半径,圆心距在它们不同位置时的数量关系:
1.⊙A和⊙B外离
d>r1+r2
2.⊙A和⊙B外切
d=r1+r2
3.⊙A和⊙B相交
r1-r2
5.⊙A和⊙B内含
d=r1-r2
d
当0102= 8cm时,两圆的位置关是 .
当0102= 2cm时,两圆的位置关是 .
当0102= 10cm时,两圆的位置关是 .
1、看谁答得快
1)两圆有两个交点,则两圆的位置关系是 .
两圆没有交点,则两圆的位置关系是 .
两圆只有一个交点,则两圆的位置关系是 .
3) 当两圆外切, 0102= 10,r1=4时,r2= .
当两圆内切, 0102= 2,r1=5时,r2 = .
学以致用
如图,⊙O与⊙P分别相切于点A和点B, 则此图是对称图行吗,如果是,画出它的对称轴。
A
B
P
O
动脑筋
相切两圆的性质
1、通过两圆圆心的直线叫做连心线。
2、如果两个圆相切,那么切点一定
在连心线上。
连心线:是指通过两圆圆心的一条直线。
分析:连心线是它的对称轴。两圆相切时,由
于切点是它们唯一的公共点,所以切点一定在对
称轴上。
例1 如图,⊙O的半径为5 cm,点P是⊙O外一点,OP=8 cm.以P点为圆心作⊙P与⊙O相切, 则⊙P的半径是多少
解:(1)设⊙O与⊙P外切于点A,
则 PA=OP-OA
所以PA=3 cm,
(2)设⊙O与⊙P内切于点B,
则 PB=PO+OB
所以PB=13 cm.
A
B
P
O
应 用
例2 已知两圆半径分别为3和4,圆心的坐标分别是(0,3)和(4,0),试判断这两圆的位置关系.
应 用
y
x
练习
1、举出一些能表示两个圆不同位置关系的实例。
2、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,设
(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)外离 (2)外切
(3)相交 (4)内切
(5)内含 (6)同心圆
3.定圆⊙O半径为3cm,动圆⊙P半径为1cm.
当两圆 时,OP为 cm?点P可以在什么样的线上运动?
O
P
外切
内切
当两圆相切时,OP为多少?
动脑筋
两个等圆有那几种位置关系?
(外离.外切.相交.重合)
圆与圆的位置关系(从公共点个数看)
(没有公共点)
(有1个公共点)
(有2个公共点)
相离
外离
内含
特殊情况
同心圆
相切
外切
内切
相交
圆与圆的五种位置关系
相交
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r
两圆内含 0≤ d
性质
判定
两圆位置关系的性质与判定:
课堂检测
1、已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距0102=7cm,则两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内切
2、已知与外切,它们的半径分别为2和3,则圆心距d的长是( )
A.d=1 B.d=5 C.1<d<5 D.d>5
3、两圆的圆心距为3,两圆的半径分别是方程的两个根,则两圆的位置关系是 ( )
课堂检测
4、如图,⊙O的半径为5cm,点P是⊙O外一点,OP
=8cm,求(1)以P为圆心作⊙P与⊙O外切,圆⊙P
的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆
⊙P的半径是多少?
P
A
B
O
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
