人教版八年级数学下册同步教学培优讲练 第十六章 二次根式:二次根式的混合运算(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册同步教学培优讲练 第十六章 二次根式:二次根式的混合运算(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 43.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览

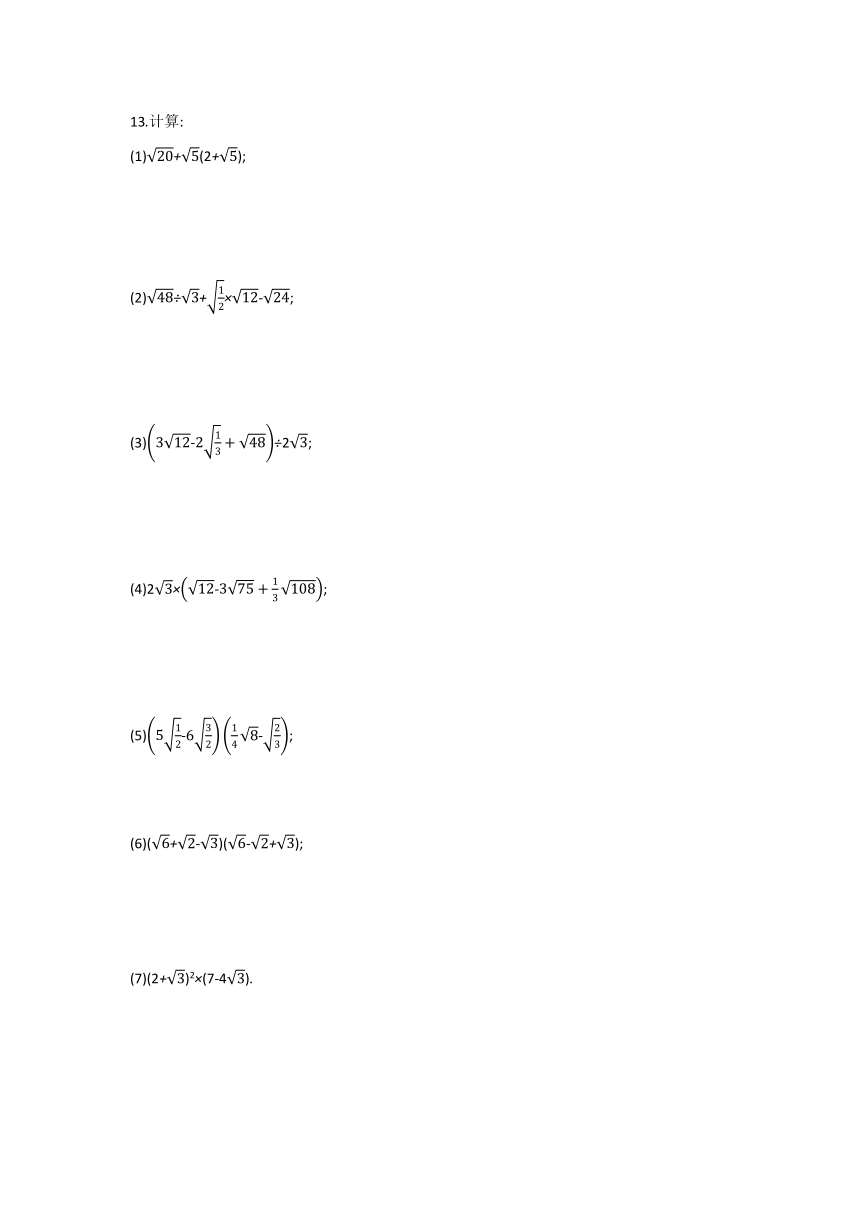
文档简介
人教版2020-2021学年八年级数学下册同步教学
第十六章 二次根式
课时作业:二次根式的混合运算
一、选择题
1.[2020·深圳期中] 下列计算正确的是 ( )
A.23+32=53 B.8÷2=2 C.52×53=56 D.43-3=4
2.计算515-20-245÷(-5)的结果为 ( )
A.-5 B.5 C.7 D.-7
3.[2019·聊城] 下列各式不成立的是 ( )
A.18-89=73 2 B.2+23=223
C.8+182=4+9=5 D.13+2=3-2
4.[2020·荆州] 若x为实数,在“(3+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是 ( )
A.3+1 B.3-1
C.23 D.1-3
5.已知x=5-12,y=5+12,则x2+xy+y2的值为( )
A.2 B.4 C.5 D.7
二、填空题
6.[2020·营口] (32+6)(32-6)= .?
7.[2020·遂宁期末] 计算:24×13-4×18= .?
8.计算:40+55= .?
9.计算:(3-2)2020×(3+2)2021= .?
10.按图K-6-1所示的程序计算,若开始输入n的值为3,则最后输出的结果是 .?
11.已知x 1=5+26,x 2=5-26,则x12+x22= .?
12.若x=1-2,y=1+2,则x2+y2-xy-2x+2y的值为 .
三、解答题
13.计算:
(1)20+5(2+5);
(2)48÷3+12×12-24;
(3)312-213+48÷23;
(4)23×12-375+13108;
(5)512-632148-23;
(6)(6+2-3)(6-2+3);
(7)(2+3)2×(7-43).
14.计算:(3+1)×3-1+27-212+|-23|+12-3.
15.一个长方形相邻两边的长分别为23+2和23-2,求这个长方形的周长和面积.
16.[阅读理解] 阅读下列材料,然后回答问题:
在进行二次根式的运算时,我们有时会碰上如35,23,23+1一样的式子,其实我们还可以将其进一步化简:
35=3×55×5=35 5;(一)
23=2×33×3=63;(二)
23+1=2×(3-1)(3+1)(3-1)=2(3-1)(3)2-12=3-1.(三)
以上这种化简的步骤叫做分母有理化.
23+1还可以用以下方法化简:
23+1=3-13+1=(3)2-123+1=(3+1)(3-1)3+1=3-1.(四)
(1)请按下列要求化简:25+3.
①参照(三)式化简25+3;
②参照(四)式化简25+3.
(2)化简:13+1+15+3+17+5+…+12n+1+2n-1(n为大于1的自然数).
人教版2020-2021学年八年级数学下册同步教学
第十六章 二次根式
课时作业:二次根式的混合运算
(参考答案)
1.B
2.C [解析] 原式=(5-25-65)÷(-5)=-75÷(-5)=7.故选C.
3.C
4.C [解析] A选项,(3+1)-(3+1)=0,故A选项不合题意;
B选项,(3+1)(3-1)=2,故B选项不合题意;
C选项,(3+1)与23无论是相加、相减、相乘、相除,结果都是无理数,故C选项符合题意;
D选项,(3+1)(1-3)=-2,故D选项不合题意.
故选C.
5.B [解析] 因为x-y=-1,xy=(5)2-14=1,所以原式=(x-y)2+3xy=(-1)2+3×1=4.故选B.
6.12 [解析] 原式=(32)2-(6)2=18-6=12.
7.2 [解析] 原式=24×13-4×24=22-2=2.
8.22+1
9.3+2 [解析] 原式=[(3-2)×(3+2)]2020×(3+2)=3+2.
10.27+163
11.98 [解析] 由题意可知x1+x2=10,x1·x2=1,所以x12+x22=(x1+x2)2-2x1·x2=100-2=98.
12.7+4 2 [解析] 因为x=1-2,y=1+2,所以x-y=(1-2)-(1+2)=-22,xy=(1-2)(1+2)=-1,
所以x2+y2-xy-2x+2y=(x-y)2-2(x-y)+xy=(-22)2-2×(-22)+(-1)=7+42.
13.解:(1)原式=25+25+5=45+5.
(2)原式=48÷3+12×12-26=4+6-26=4-6.
(3)原式=63-233+43÷23=283 3÷23=143.
(4)原式=236-6225+2332×36=12-90+12=-66.
(5)原式=54 12×8-512×23-64 32×8+632×23=54×2-5×33-32×23+6=52-53 3-33+6=172-143 3.
(6)原式=62-2-32=6-(5-26)=6-5+26=1+26.
(7)原式=(7+43)(7-43)=72-(43)2=49-48=1.
14.解:原式=3+3-1+33-33+23+8=10+1733.
15.解:这个长方形的周长为(23+2+23-2)×2=83,
面积为(23+2)×(23-2)=(23)2-(2)2=10.
16.解:(1)①25+3=2(5-3)(5+3)(5-3)=
2(5-3)(5)2-(3)2=5-3.
②25+3=5-35+3=(5)2-(3)25+3=
(5+3)(5-3)5+3=5-3.
(2)原式=3-1(3+1)(3-1)+5-3(5+3)(5-3)+7-5(7+5)(7-5)+…+2n+1-2n-1(2n+1+2n-1)(2n+1-2n-1)
=3-12+5-32+7-52+…+2n+1-2n-12
=2n+1-12.
第十六章 二次根式
课时作业:二次根式的混合运算
一、选择题
1.[2020·深圳期中] 下列计算正确的是 ( )
A.23+32=53 B.8÷2=2 C.52×53=56 D.43-3=4
2.计算515-20-245÷(-5)的结果为 ( )
A.-5 B.5 C.7 D.-7
3.[2019·聊城] 下列各式不成立的是 ( )
A.18-89=73 2 B.2+23=223
C.8+182=4+9=5 D.13+2=3-2
4.[2020·荆州] 若x为实数,在“(3+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是 ( )
A.3+1 B.3-1
C.23 D.1-3
5.已知x=5-12,y=5+12,则x2+xy+y2的值为( )
A.2 B.4 C.5 D.7
二、填空题
6.[2020·营口] (32+6)(32-6)= .?
7.[2020·遂宁期末] 计算:24×13-4×18= .?
8.计算:40+55= .?
9.计算:(3-2)2020×(3+2)2021= .?
10.按图K-6-1所示的程序计算,若开始输入n的值为3,则最后输出的结果是 .?
11.已知x 1=5+26,x 2=5-26,则x12+x22= .?
12.若x=1-2,y=1+2,则x2+y2-xy-2x+2y的值为 .
三、解答题
13.计算:
(1)20+5(2+5);
(2)48÷3+12×12-24;
(3)312-213+48÷23;
(4)23×12-375+13108;
(5)512-632148-23;
(6)(6+2-3)(6-2+3);
(7)(2+3)2×(7-43).
14.计算:(3+1)×3-1+27-212+|-23|+12-3.
15.一个长方形相邻两边的长分别为23+2和23-2,求这个长方形的周长和面积.
16.[阅读理解] 阅读下列材料,然后回答问题:
在进行二次根式的运算时,我们有时会碰上如35,23,23+1一样的式子,其实我们还可以将其进一步化简:
35=3×55×5=35 5;(一)
23=2×33×3=63;(二)
23+1=2×(3-1)(3+1)(3-1)=2(3-1)(3)2-12=3-1.(三)
以上这种化简的步骤叫做分母有理化.
23+1还可以用以下方法化简:
23+1=3-13+1=(3)2-123+1=(3+1)(3-1)3+1=3-1.(四)
(1)请按下列要求化简:25+3.
①参照(三)式化简25+3;
②参照(四)式化简25+3.
(2)化简:13+1+15+3+17+5+…+12n+1+2n-1(n为大于1的自然数).
人教版2020-2021学年八年级数学下册同步教学
第十六章 二次根式
课时作业:二次根式的混合运算
(参考答案)
1.B
2.C [解析] 原式=(5-25-65)÷(-5)=-75÷(-5)=7.故选C.
3.C
4.C [解析] A选项,(3+1)-(3+1)=0,故A选项不合题意;
B选项,(3+1)(3-1)=2,故B选项不合题意;
C选项,(3+1)与23无论是相加、相减、相乘、相除,结果都是无理数,故C选项符合题意;
D选项,(3+1)(1-3)=-2,故D选项不合题意.
故选C.
5.B [解析] 因为x-y=-1,xy=(5)2-14=1,所以原式=(x-y)2+3xy=(-1)2+3×1=4.故选B.
6.12 [解析] 原式=(32)2-(6)2=18-6=12.
7.2 [解析] 原式=24×13-4×24=22-2=2.
8.22+1
9.3+2 [解析] 原式=[(3-2)×(3+2)]2020×(3+2)=3+2.
10.27+163
11.98 [解析] 由题意可知x1+x2=10,x1·x2=1,所以x12+x22=(x1+x2)2-2x1·x2=100-2=98.
12.7+4 2 [解析] 因为x=1-2,y=1+2,所以x-y=(1-2)-(1+2)=-22,xy=(1-2)(1+2)=-1,
所以x2+y2-xy-2x+2y=(x-y)2-2(x-y)+xy=(-22)2-2×(-22)+(-1)=7+42.
13.解:(1)原式=25+25+5=45+5.
(2)原式=48÷3+12×12-26=4+6-26=4-6.
(3)原式=63-233+43÷23=283 3÷23=143.
(4)原式=236-6225+2332×36=12-90+12=-66.
(5)原式=54 12×8-512×23-64 32×8+632×23=54×2-5×33-32×23+6=52-53 3-33+6=172-143 3.
(6)原式=62-2-32=6-(5-26)=6-5+26=1+26.
(7)原式=(7+43)(7-43)=72-(43)2=49-48=1.
14.解:原式=3+3-1+33-33+23+8=10+1733.
15.解:这个长方形的周长为(23+2+23-2)×2=83,
面积为(23+2)×(23-2)=(23)2-(2)2=10.
16.解:(1)①25+3=2(5-3)(5+3)(5-3)=
2(5-3)(5)2-(3)2=5-3.
②25+3=5-35+3=(5)2-(3)25+3=
(5+3)(5-3)5+3=5-3.
(2)原式=3-1(3+1)(3-1)+5-3(5+3)(5-3)+7-5(7+5)(7-5)+…+2n+1-2n-1(2n+1+2n-1)(2n+1-2n-1)
=3-12+5-32+7-52+…+2n+1-2n-12
=2n+1-12.
