北师大版九年级下册 第3章 《圆》高频考点专题训练(一)(Word版 含答案)
文档属性
| 名称 | 北师大版九年级下册 第3章 《圆》高频考点专题训练(一)(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 23:26:13 | ||
图片预览


文档简介
第3章 《圆》高频考点专题训练(一)
一.选择题
1.下列说法正确的是( )
A.三点确定一个圆
B.同圆中,圆周角等于圆心角的一半
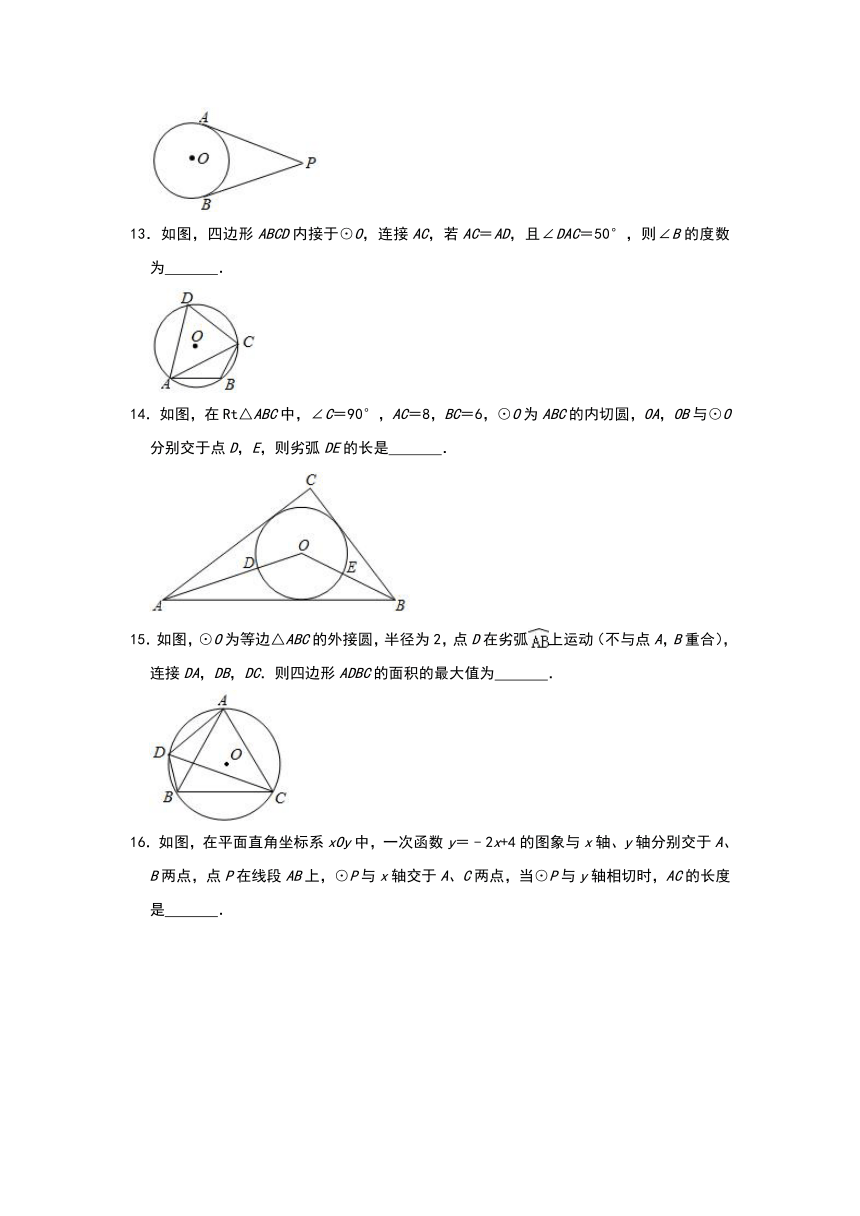
C.平分弦的直径垂直于弦
D.一个三角形只有一个外接圆
2.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
3.如图,AB是⊙O的直径,C是⊙O上一点,AC=8,BC=6,CD平分∠ACB交⊙O于点D,则劣弧AD的长为( )
A.π B.π C.2π D.π
4.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
5.如图,在平面直角坐标系中,A(﹣2,2),B(8,2),C(6,6),点P为△ABC的外接圆的圆心,将△ABC绕点O逆时针旋转90°,点P的对应点P′的坐标为( )
A.(﹣2,3) B.(﹣3,2) C.(2,﹣3) D.(3,﹣2)
6.如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D为的中点,DM⊥AC于M,则DM的长为( )
A. B. C.1 D.
7.如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为( )
A.4 B.2 C. D.
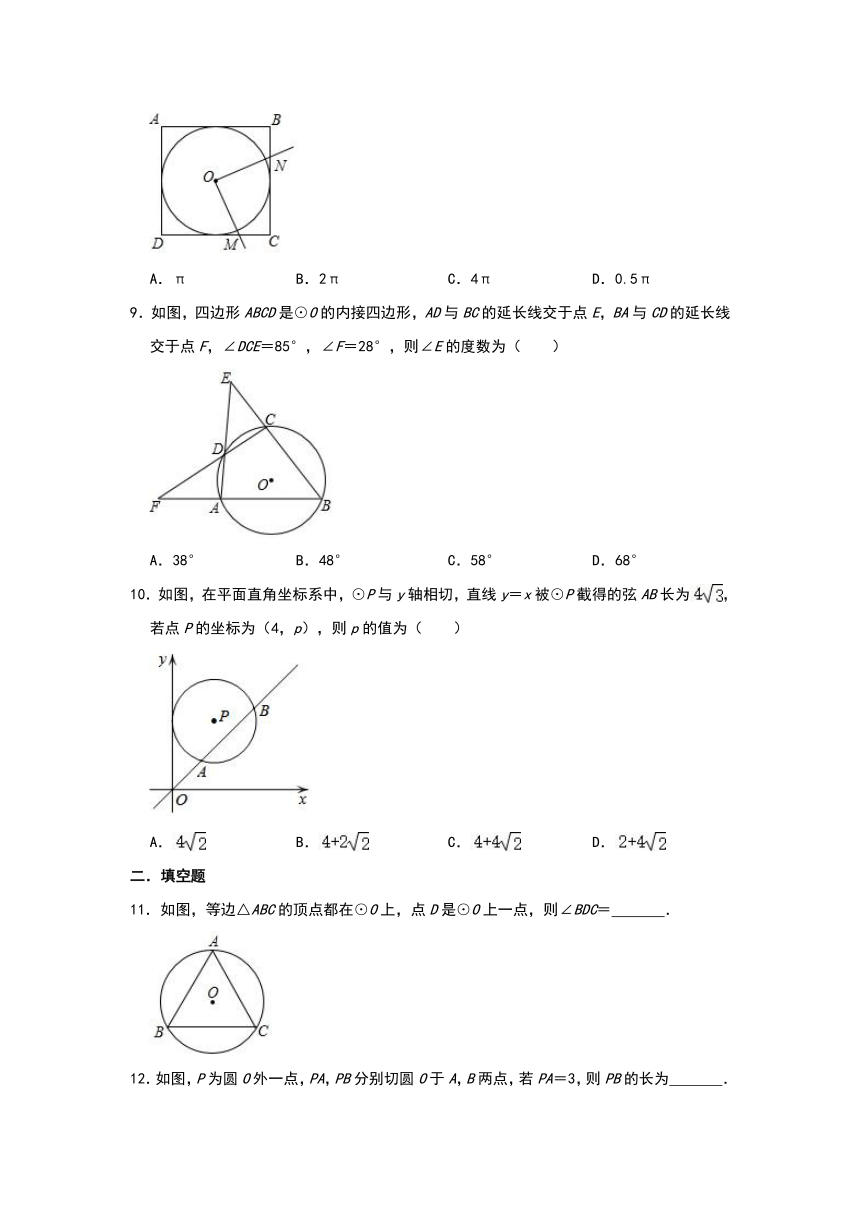
8.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
9.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=85°,∠F=28°,则∠E的度数为( )
A.38° B.48° C.58° D.68°
10.如图,在平面直角坐标系中,⊙P与y轴相切,直线y=x被⊙P截得的弦AB长为,若点P的坐标为(4,p),则p的值为( )
A. B. C. D.
二.填空题
11.如图,等边△ABC的顶点都在⊙O上,点D是⊙O上一点,则∠BDC= .
12.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB的长为 .
13.如图,四边形ABCD内接于⊙O,连接AC,若AC=AD,且∠DAC=50°,则∠B的度数为 .
14.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为ABC的内切圆,OA,OB与⊙O分别交于点D,E,则劣弧DE的长是 .
15.如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B重合),连接DA,DB,DC.则四边形ADBC的面积的最大值为 .
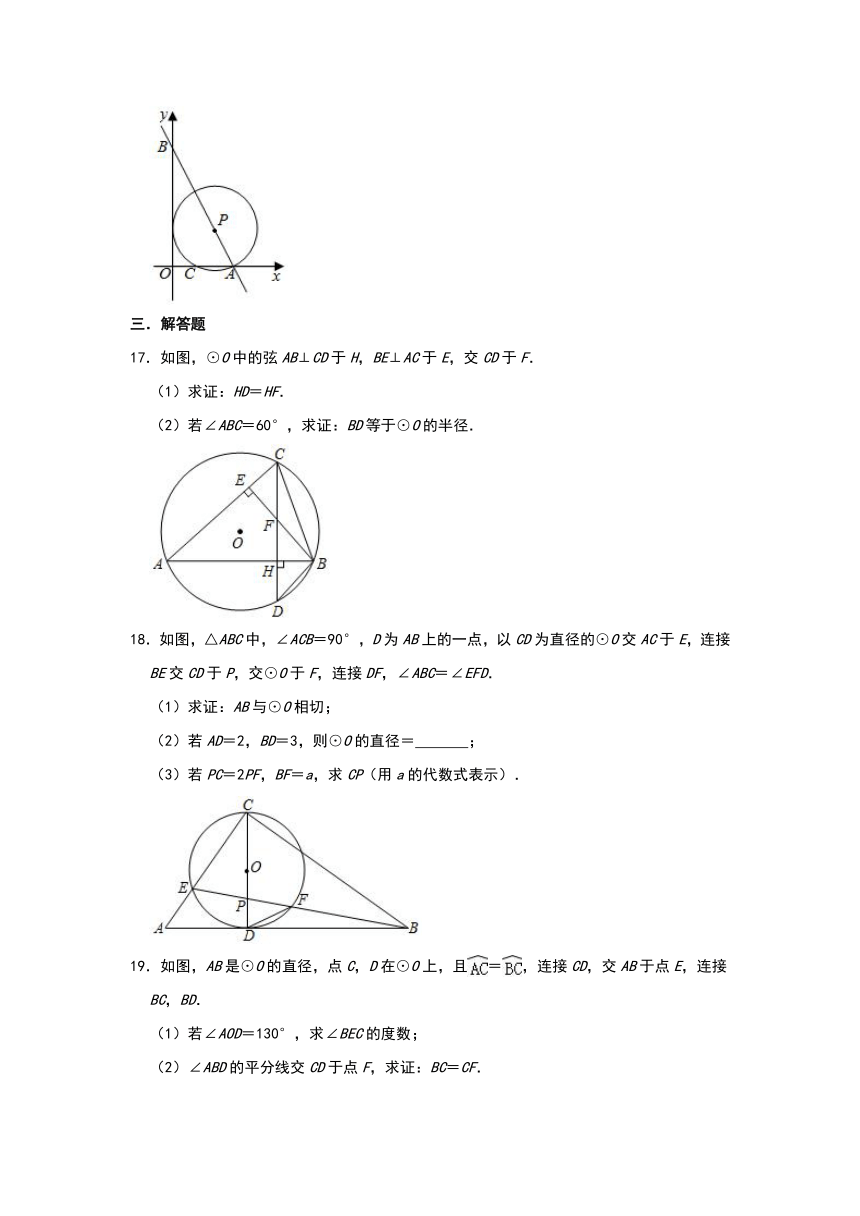
16.如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是 .
三.解答题
17.如图,⊙O中的弦AB⊥CD于H,BE⊥AC于E,交CD于F.
(1)求证:HD=HF.
(2)若∠ABC=60°,求证:BD等于⊙O的半径.
18.如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.
(1)求证:AB与⊙O相切;
(2)若AD=2,BD=3,则⊙O的直径= ;
(3)若PC=2PF,BF=a,求CP(用a的代数式表示).
19.如图,AB是⊙O的直径,点C,D在⊙O上,且=,连接CD,交AB于点E,连接BC,BD.
(1)若∠AOD=130°,求∠BEC的度数;
(2)∠ABD的平分线交CD于点F,求证:BC=CF.
20.国庆假期,小明做数学题时遇到了如下问题:
如图1,四边形ABCD是⊙O的内接四边形,BC是⊙O的直径,直线l经过点A,∠ABD=∠DAE=30°.试说明直线l与⊙O相切.
小明添加了适当的辅助线后,得到了图2的图形,并利用它解决了问题.
(1)请你根据小明的思考,写出解决这一问题的过程;
(2)图2中,若AD=,AB=4,求DC的长.
21.在Rt△ABC中,∠A=90°,AB=AC=4,O是BC边上的点且⊙O与AB、AC都相切,切点分别为D、E.
(1)求⊙O的半径;
(2)如果F为上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;
(3)探究:在(2)的条件下,设BG=x,CH=y,试问y与x之间满足怎样的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.
参考答案
一.选择题
1.解:A、平面内不共线的三点确定一个圆,所以A错误;
B、在同圆或等圆中,同弧所对的圆周角等于它所对的圆心角的一半,所以B错误;
C、平分弦(非直径)的直径垂直于弦,所以C错误;
D、三角形的外心到三角形各个顶点的距离都相等,所以D正确.
故选:D.
2.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
3.解:连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,AC=8,BC=6,由勾股定理得AB=10,
∴AO=5,
∵CD平分∠ACB,
∴∠ACD=∠ACB=45°,
由圆周角定理得∠AOD=2∠ACD=90°,
∴劣弧AD的长为=π.
故选:D.
4.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
5.解:如图,
过点C作CD⊥AB于点D,
∵A(﹣2,2),B(8,2),C(6,6),
∴D(6,2)
∴AB=10,BD=2,CD=4
∴BC2=BD2+CD2=20
AD=8,
∴AC2=CD2+AD2=80
∴AB2=BC2+AC2
∴△ABC是直角三角形
∴△ABC的外接圆的圆心P在斜边AB的中点处
如图,取AB的中点P,
∴P(3,2),
连接OP,将OP绕点O逆时针旋转90至P′,
作PG⊥x轴于点G,P′H⊥x轴于点H,
∴∠PGO=∠P′HO=90°
∴∠POG=∠OP′H,
OP=OP′
∴△OPG≌△P′OH(AAS)
∴OH=PG=2,P′H=OG=3
∴P′(﹣2,3).
故选:A.
6.解:如图,连接OD交AC于H,连接BC.
∵AB是直径,
∴∠ACB=90°,
∴BC==6,
∵=,
∴OD⊥AB,
∵∠OAH=∠CAB,∠AOH=∠ACB=90°,
∴△AOH∽△ACB,
∴==
∴==
∴OH=,AH=,
∵DH=OD﹣OH=5﹣=,
∵DM⊥AC,
∵∠DMH=∠AOH=90°,∠DHM=∠AHO,
∴△DMH∽△AOH,
∴=,
∴=,
∴DM=1,
故选:C.
7.解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故选:D.
8.解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,
连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=NF,
∴CM+CN=CE+CF=4,
∴OE=2,
∴⊙O的面积为4π,
故选:C.
9.解:∠B=∠DCE﹣∠F=57°,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B=57°,
∴∠E=180°﹣∠DCE﹣∠EDC=38°,
故选:A.
10.解:如图,作PF⊥x轴于F,交AB于D,作PE⊥AB于E,连结PB,
∵⊙P与y轴相切于点C,⊙P的半径是4,
∴OF=4,
把x=4代入y=x得y=4,
∴D点坐标为(4,4),
∴DF=4,
∴△ODF为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=4,
∴PE==2,
∴PD=PE=2,
∴PF=PD+DF=4+2,
∴p=4+2,
故选:B.
二.填空题(共6小题)
11.解:∵△ABC为等边三角形,
∴∠BAC=60°,
当点在上,如图1,∠BDC=∠BAC=60°;
当点在上,如图2,∵∠BDC+∠BAC=180°,
∴∠BDC=180°﹣60°=120°,
综上所述,∠BDC的度数为60°或120°.
故答案为60°或120°.
12.解:∵PA,PB分别切圆O于A,B两点,
∴PB=PA=3.
故答案为3.
13.解:∵AC=AD,且∠DAC=50°,
∴∠D=∠ACD==65°,
∴∠B=180°﹣∠D=180°﹣65°=115°,
故答案为:115°.
14.解:∵∠C=90°,AC=8,BC=6,
∴AB==10,
∵⊙O为ABC的内切圆,
∴OD==2,OB平分∠BAC,OC平分∠ABC,
∴∠AOB=90°+∠C=90°+×90°=135°,
∴劣弧DE的长==π.
故答案为π.
15.解:如图,将△ADC绕点C逆时针旋转60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线,
∵DC=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=CD2,
∴当CD最大时,四边形ADBC的面积最大,
∴当CD为⊙O的直径时,CD的值最大,
即CD=4,
∴四边形ADBC的面积的最大值为CD2=4,
故答案为:4.
16.解:∵一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,
∴A(2,0),B(0,4),
∴OA=2,OB=4,
如图,设⊙P与y轴相切于点D,连接PD,
∴PD⊥OB,
∵OA⊥OB,
∴PD∥OA,
∴==,
设PD=PC=x,则BD=2x,
∴OD=OB﹣BD=4﹣2x,
作PE⊥OA于点E,
∴四边形OEPD是矩形,
∴PD=OE=x,PE=OD=4﹣2x,
∴AE=CE=OA﹣OE=2﹣x,
∴PC2=PE2+CE2,
∴x2=(4﹣2x)2+(2﹣x)2,
解得x=,
∵>2,不符合题意舍去,
∴x=,
∵PE⊥AC,根据垂径定理,得
AC=2AE=2(2﹣x)=4﹣(5﹣)=﹣1.
故答案为:﹣1.
三.解答题(共5小题)
17.证明:(1)∵CH⊥AB,
∴∠BFH+∠FBH=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,
∴∠BFH=∠A,
∵∠A=∠D,
∴∠BFH=∠D,
∴BF=BD,
∵BH⊥FD,
∴HD=HF;
(2)连接OD、OB,如图,
∵∠BCD+∠CBH=90°,
∴∠BCH=90°﹣∠CBH=90°﹣60°=30°,
∴∠BOD=2∠BCD=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB,
∴BD等于⊙O的半径.
18.(1)证明:∵∠ACB=90°,
∴∠CEB+∠CBE=90°,
∵∠ABC=∠EFD,∠EFD=∠FDB+∠FBD,
∴∠EBC=∠FDB,
∵∠CEB=∠CDF,
∴∠CDF+∠FDB=90°,
即∠CDB=90°,
∴CD⊥AB,
∴AB与⊙O相切;
(2)解:∵∠ACD+∠A=90°,∠A+∠ABC=90°,
∴∠ACD=∠ABC,
∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴=,
∴CD2=AD?BD=2×3=6,
∴CD=,
∴⊙O的直径为,
故答案为:.
(3)解:∵CD为⊙O的直径,
∴∠CFD=90°,
∴∠DCF+∠CDF=90°,
又∵∠CDB=90°,
∴∠FDB+∠CDF=90°,
∴∠FDB=∠DCF,
∵∠EBC=∠FDB,
∴∠EBC=∠DCF,
∴△PCF∽△PBC,
∴=,
∵PC=2PF,
∴==
∴PB=2PC=4PF,
又PB=PF+BF,
∴4PF=PF+BF,
∴PF=BF=a,
∵PC=2PF.
∴PC=a.
19.解:(1)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=,
∴∠A=∠ABC=45°,
∵∠AOD=130°,
∴∠ACD=65°,
∵∠BEC是△ACE的外角,
∴∠BEC=∠A+∠ACD=110°.
(2)证明:∵BF平分∠ABD,
∴∠EBF=∠DBF,
∵,
∴∠ABC=∠CDB,
又∵∠CFB=∠FBD+∠FDB,∠CBF=∠ABC+∠EBF,
∴∠CBF=∠CFB,
∴CF=BC.
20.(1)证明:过A作直径AF,连接DF,如图2所示:
∵AF是⊙O的直径,
∴∠ADF=90°,
∴∠AFD+∠FAD=90°,
∵∠ABD=∠AFD,∠ABD=∠DAE,
∴∠AFD=∠DAE,
∴∠DAE+∠DAF=90°,
即∠OAE=90°,
∴OA⊥AE,
∵点A是半径OA的外端,
∴直线l与⊙O相切;
(2)解:过点A作AG⊥BD,垂足为点G,
∴∠AGB=∠AGD=90°,
∵∠ABD=30°,
∴∠AFD=30°,
∴直径AF=2AD==BC,
∵∠ABD=30°,AB=4,
∴AG==2,BG=AG=2,
∴DG===,
∴BD=BG+DG=,
∵BC是直径,
∴∠BDC=90°,
∴.
21.解:(1)连接OD、OE、OA,
∵O是BC边上的点且⊙O与AB、AC都相切,
∴OD⊥AB,AC⊥OE,
又∵∠BAC=90°,且OD=OE,
∴四边形ADOE为正方形,
∴OE=AE,
∴∠OAE=45°;
又∵∠C=45°,
∴OE=2,△OAC为等腰直角三角形,
AE=EC=AC=×4=2,即⊙O的半径是2;
(2)②的结论正确;理由如下:
连接OF、OG、OH,
由题意,GD、GF以及HF、HE与圆相切,
所以GD=GF,HE=HF,∠DOG=∠FOG,∠FOH=∠HOE,
而∠DOE=90°,所以可以得到∠GOH==45°.
(3)BG=x,CH=y,
易得:GF=GD=x﹣2,FH=HE=y﹣2,AG=4﹣x,AE=4﹣y,
所以GH=x+y﹣4,
由∠A=90°,可得GH2=AG2+AH2,代入上述各数值,
化简可得y=,由AG≥0,AE≥0,可得x≤4,y≤4,所以2≤x≤4,
当x=y时,有AG=AH,由于AB=AC所以可得GH与BC平行,连接AO,
设AO交GH于F',有∠OFH=90°,
所以F'为切点F,即F为AO与圆的交点同时F是的中点.
一.选择题
1.下列说法正确的是( )
A.三点确定一个圆
B.同圆中,圆周角等于圆心角的一半
C.平分弦的直径垂直于弦
D.一个三角形只有一个外接圆
2.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
3.如图,AB是⊙O的直径,C是⊙O上一点,AC=8,BC=6,CD平分∠ACB交⊙O于点D,则劣弧AD的长为( )
A.π B.π C.2π D.π
4.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
5.如图,在平面直角坐标系中,A(﹣2,2),B(8,2),C(6,6),点P为△ABC的外接圆的圆心,将△ABC绕点O逆时针旋转90°,点P的对应点P′的坐标为( )
A.(﹣2,3) B.(﹣3,2) C.(2,﹣3) D.(3,﹣2)
6.如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D为的中点,DM⊥AC于M,则DM的长为( )
A. B. C.1 D.
7.如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为( )
A.4 B.2 C. D.
8.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
9.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=85°,∠F=28°,则∠E的度数为( )
A.38° B.48° C.58° D.68°
10.如图,在平面直角坐标系中,⊙P与y轴相切,直线y=x被⊙P截得的弦AB长为,若点P的坐标为(4,p),则p的值为( )
A. B. C. D.
二.填空题
11.如图,等边△ABC的顶点都在⊙O上,点D是⊙O上一点,则∠BDC= .
12.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB的长为 .
13.如图,四边形ABCD内接于⊙O,连接AC,若AC=AD,且∠DAC=50°,则∠B的度数为 .
14.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为ABC的内切圆,OA,OB与⊙O分别交于点D,E,则劣弧DE的长是 .
15.如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B重合),连接DA,DB,DC.则四边形ADBC的面积的最大值为 .
16.如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是 .
三.解答题
17.如图,⊙O中的弦AB⊥CD于H,BE⊥AC于E,交CD于F.
(1)求证:HD=HF.
(2)若∠ABC=60°,求证:BD等于⊙O的半径.
18.如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.
(1)求证:AB与⊙O相切;
(2)若AD=2,BD=3,则⊙O的直径= ;
(3)若PC=2PF,BF=a,求CP(用a的代数式表示).
19.如图,AB是⊙O的直径,点C,D在⊙O上,且=,连接CD,交AB于点E,连接BC,BD.
(1)若∠AOD=130°,求∠BEC的度数;
(2)∠ABD的平分线交CD于点F,求证:BC=CF.
20.国庆假期,小明做数学题时遇到了如下问题:
如图1,四边形ABCD是⊙O的内接四边形,BC是⊙O的直径,直线l经过点A,∠ABD=∠DAE=30°.试说明直线l与⊙O相切.
小明添加了适当的辅助线后,得到了图2的图形,并利用它解决了问题.
(1)请你根据小明的思考,写出解决这一问题的过程;
(2)图2中,若AD=,AB=4,求DC的长.
21.在Rt△ABC中,∠A=90°,AB=AC=4,O是BC边上的点且⊙O与AB、AC都相切,切点分别为D、E.
(1)求⊙O的半径;
(2)如果F为上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;
(3)探究:在(2)的条件下,设BG=x,CH=y,试问y与x之间满足怎样的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.
参考答案
一.选择题
1.解:A、平面内不共线的三点确定一个圆,所以A错误;
B、在同圆或等圆中,同弧所对的圆周角等于它所对的圆心角的一半,所以B错误;
C、平分弦(非直径)的直径垂直于弦,所以C错误;
D、三角形的外心到三角形各个顶点的距离都相等,所以D正确.
故选:D.
2.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
3.解:连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,AC=8,BC=6,由勾股定理得AB=10,
∴AO=5,
∵CD平分∠ACB,
∴∠ACD=∠ACB=45°,
由圆周角定理得∠AOD=2∠ACD=90°,
∴劣弧AD的长为=π.
故选:D.
4.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
5.解:如图,
过点C作CD⊥AB于点D,
∵A(﹣2,2),B(8,2),C(6,6),
∴D(6,2)
∴AB=10,BD=2,CD=4
∴BC2=BD2+CD2=20
AD=8,
∴AC2=CD2+AD2=80
∴AB2=BC2+AC2
∴△ABC是直角三角形
∴△ABC的外接圆的圆心P在斜边AB的中点处
如图,取AB的中点P,
∴P(3,2),
连接OP,将OP绕点O逆时针旋转90至P′,
作PG⊥x轴于点G,P′H⊥x轴于点H,
∴∠PGO=∠P′HO=90°
∴∠POG=∠OP′H,
OP=OP′
∴△OPG≌△P′OH(AAS)
∴OH=PG=2,P′H=OG=3
∴P′(﹣2,3).
故选:A.
6.解:如图,连接OD交AC于H,连接BC.
∵AB是直径,
∴∠ACB=90°,
∴BC==6,
∵=,
∴OD⊥AB,
∵∠OAH=∠CAB,∠AOH=∠ACB=90°,
∴△AOH∽△ACB,
∴==
∴==
∴OH=,AH=,
∵DH=OD﹣OH=5﹣=,
∵DM⊥AC,
∵∠DMH=∠AOH=90°,∠DHM=∠AHO,
∴△DMH∽△AOH,
∴=,
∴=,
∴DM=1,
故选:C.
7.解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故选:D.
8.解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,
连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=NF,
∴CM+CN=CE+CF=4,
∴OE=2,
∴⊙O的面积为4π,
故选:C.
9.解:∠B=∠DCE﹣∠F=57°,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B=57°,
∴∠E=180°﹣∠DCE﹣∠EDC=38°,
故选:A.
10.解:如图,作PF⊥x轴于F,交AB于D,作PE⊥AB于E,连结PB,
∵⊙P与y轴相切于点C,⊙P的半径是4,
∴OF=4,
把x=4代入y=x得y=4,
∴D点坐标为(4,4),
∴DF=4,
∴△ODF为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=4,
∴PE==2,
∴PD=PE=2,
∴PF=PD+DF=4+2,
∴p=4+2,
故选:B.
二.填空题(共6小题)
11.解:∵△ABC为等边三角形,
∴∠BAC=60°,
当点在上,如图1,∠BDC=∠BAC=60°;
当点在上,如图2,∵∠BDC+∠BAC=180°,
∴∠BDC=180°﹣60°=120°,
综上所述,∠BDC的度数为60°或120°.
故答案为60°或120°.
12.解:∵PA,PB分别切圆O于A,B两点,
∴PB=PA=3.
故答案为3.
13.解:∵AC=AD,且∠DAC=50°,
∴∠D=∠ACD==65°,
∴∠B=180°﹣∠D=180°﹣65°=115°,
故答案为:115°.
14.解:∵∠C=90°,AC=8,BC=6,
∴AB==10,
∵⊙O为ABC的内切圆,
∴OD==2,OB平分∠BAC,OC平分∠ABC,
∴∠AOB=90°+∠C=90°+×90°=135°,
∴劣弧DE的长==π.
故答案为π.
15.解:如图,将△ADC绕点C逆时针旋转60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线,
∵DC=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=CD2,
∴当CD最大时,四边形ADBC的面积最大,
∴当CD为⊙O的直径时,CD的值最大,
即CD=4,
∴四边形ADBC的面积的最大值为CD2=4,
故答案为:4.
16.解:∵一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,
∴A(2,0),B(0,4),
∴OA=2,OB=4,
如图,设⊙P与y轴相切于点D,连接PD,
∴PD⊥OB,
∵OA⊥OB,
∴PD∥OA,
∴==,
设PD=PC=x,则BD=2x,
∴OD=OB﹣BD=4﹣2x,
作PE⊥OA于点E,
∴四边形OEPD是矩形,
∴PD=OE=x,PE=OD=4﹣2x,
∴AE=CE=OA﹣OE=2﹣x,
∴PC2=PE2+CE2,
∴x2=(4﹣2x)2+(2﹣x)2,
解得x=,
∵>2,不符合题意舍去,
∴x=,
∵PE⊥AC,根据垂径定理,得
AC=2AE=2(2﹣x)=4﹣(5﹣)=﹣1.
故答案为:﹣1.
三.解答题(共5小题)
17.证明:(1)∵CH⊥AB,
∴∠BFH+∠FBH=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,
∴∠BFH=∠A,
∵∠A=∠D,
∴∠BFH=∠D,
∴BF=BD,
∵BH⊥FD,
∴HD=HF;
(2)连接OD、OB,如图,
∵∠BCD+∠CBH=90°,
∴∠BCH=90°﹣∠CBH=90°﹣60°=30°,
∴∠BOD=2∠BCD=60°,
∵OB=OD,
∴△OBD为等边三角形,
∴BD=OB,
∴BD等于⊙O的半径.
18.(1)证明:∵∠ACB=90°,
∴∠CEB+∠CBE=90°,
∵∠ABC=∠EFD,∠EFD=∠FDB+∠FBD,
∴∠EBC=∠FDB,
∵∠CEB=∠CDF,
∴∠CDF+∠FDB=90°,
即∠CDB=90°,
∴CD⊥AB,
∴AB与⊙O相切;
(2)解:∵∠ACD+∠A=90°,∠A+∠ABC=90°,
∴∠ACD=∠ABC,
∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴=,
∴CD2=AD?BD=2×3=6,
∴CD=,
∴⊙O的直径为,
故答案为:.
(3)解:∵CD为⊙O的直径,
∴∠CFD=90°,
∴∠DCF+∠CDF=90°,
又∵∠CDB=90°,
∴∠FDB+∠CDF=90°,
∴∠FDB=∠DCF,
∵∠EBC=∠FDB,
∴∠EBC=∠DCF,
∴△PCF∽△PBC,
∴=,
∵PC=2PF,
∴==
∴PB=2PC=4PF,
又PB=PF+BF,
∴4PF=PF+BF,
∴PF=BF=a,
∵PC=2PF.
∴PC=a.
19.解:(1)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=,
∴∠A=∠ABC=45°,
∵∠AOD=130°,
∴∠ACD=65°,
∵∠BEC是△ACE的外角,
∴∠BEC=∠A+∠ACD=110°.
(2)证明:∵BF平分∠ABD,
∴∠EBF=∠DBF,
∵,
∴∠ABC=∠CDB,
又∵∠CFB=∠FBD+∠FDB,∠CBF=∠ABC+∠EBF,
∴∠CBF=∠CFB,
∴CF=BC.
20.(1)证明:过A作直径AF,连接DF,如图2所示:
∵AF是⊙O的直径,
∴∠ADF=90°,
∴∠AFD+∠FAD=90°,
∵∠ABD=∠AFD,∠ABD=∠DAE,
∴∠AFD=∠DAE,
∴∠DAE+∠DAF=90°,
即∠OAE=90°,
∴OA⊥AE,
∵点A是半径OA的外端,
∴直线l与⊙O相切;
(2)解:过点A作AG⊥BD,垂足为点G,
∴∠AGB=∠AGD=90°,
∵∠ABD=30°,
∴∠AFD=30°,
∴直径AF=2AD==BC,
∵∠ABD=30°,AB=4,
∴AG==2,BG=AG=2,
∴DG===,
∴BD=BG+DG=,
∵BC是直径,
∴∠BDC=90°,
∴.
21.解:(1)连接OD、OE、OA,
∵O是BC边上的点且⊙O与AB、AC都相切,
∴OD⊥AB,AC⊥OE,
又∵∠BAC=90°,且OD=OE,
∴四边形ADOE为正方形,
∴OE=AE,
∴∠OAE=45°;
又∵∠C=45°,
∴OE=2,△OAC为等腰直角三角形,
AE=EC=AC=×4=2,即⊙O的半径是2;
(2)②的结论正确;理由如下:
连接OF、OG、OH,
由题意,GD、GF以及HF、HE与圆相切,
所以GD=GF,HE=HF,∠DOG=∠FOG,∠FOH=∠HOE,
而∠DOE=90°,所以可以得到∠GOH==45°.
(3)BG=x,CH=y,
易得:GF=GD=x﹣2,FH=HE=y﹣2,AG=4﹣x,AE=4﹣y,
所以GH=x+y﹣4,
由∠A=90°,可得GH2=AG2+AH2,代入上述各数值,
化简可得y=,由AG≥0,AE≥0,可得x≤4,y≤4,所以2≤x≤4,
当x=y时,有AG=AH,由于AB=AC所以可得GH与BC平行,连接AO,
设AO交GH于F',有∠OFH=90°,
所以F'为切点F,即F为AO与圆的交点同时F是的中点.
