人教版七年级数学下册 5.3 平行线的性质 同步测试题(Word版 有答案)
文档属性
| 名称 | 人教版七年级数学下册 5.3 平行线的性质 同步测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 114.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 23:29:31 | ||
图片预览




文档简介
10312400103378005.3 平行线的性质 同步测试题
班级:_____________姓名:_____________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 ) ?
1. 如图,AB?//?CD?//?EF,AF?//?CG,则图中与∠A(不包括∠A)相等的角有( )
A.1个 B.2个 C.3个 D.4个?
2. 如图所示,过点P画直线a的平行线b的作法的依据是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
?
3. 下列命题中错误的是(? ? ? ? )
A.任何一个命题都有逆命题
B.一个真命题的逆命题可能是真命题
C.一个定理不一定有逆定理
D.任何一个定理都没有逆定理?
4. 师范大学学生张丽、王云、李玲三人一起去银行柜员机取钱,张丽取款一次,王云取款两次,李玲取款三次,假设每取款一次所用时间相同,请问她们三人按什么样的顺序取款,才能使三人所花总时间最少(包括等待时间)( )
A.张丽,王云,李玲 B.李玲,张丽,王云
C.张丽,李玲,王云 D.王云,李玲,张丽
5. 甲、乙、丙三人用擂台赛形式进行训练.每局两人单打比赛,另一人当裁判.每一局输者当下一局的裁判,而原来的裁判与赢者比赛.一天训练结束时,统计甲共打12局,乙共打21局,而丙共当裁判8局.那么整个比赛中第10局的输者( )
A.必是甲 B.必是乙 C.必是丙 D.不能确定
6. 如图,直线l?//?m,将含有45?角的三角形板ABC的直角顶点C放在直线m上,若∠1=20?,则∠2的度数为(? ? ? ? )
A.20? B.25? C.30? D.35??
7. 下列语句是命题的是(? ? ? ? )
A.对角线相等吗? B.作线段AB=10cm
C.若a=b,则-a=-b D.连接A,B 两点
8. 下列句子是命题的是(? ? ? ? )
A.求1+2+3+4+5+6的值 B.过点P作PC//OA
C. 能根据等式的性质解方程吗 D. 房屋顶棚是彩钢做的
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 ) ?
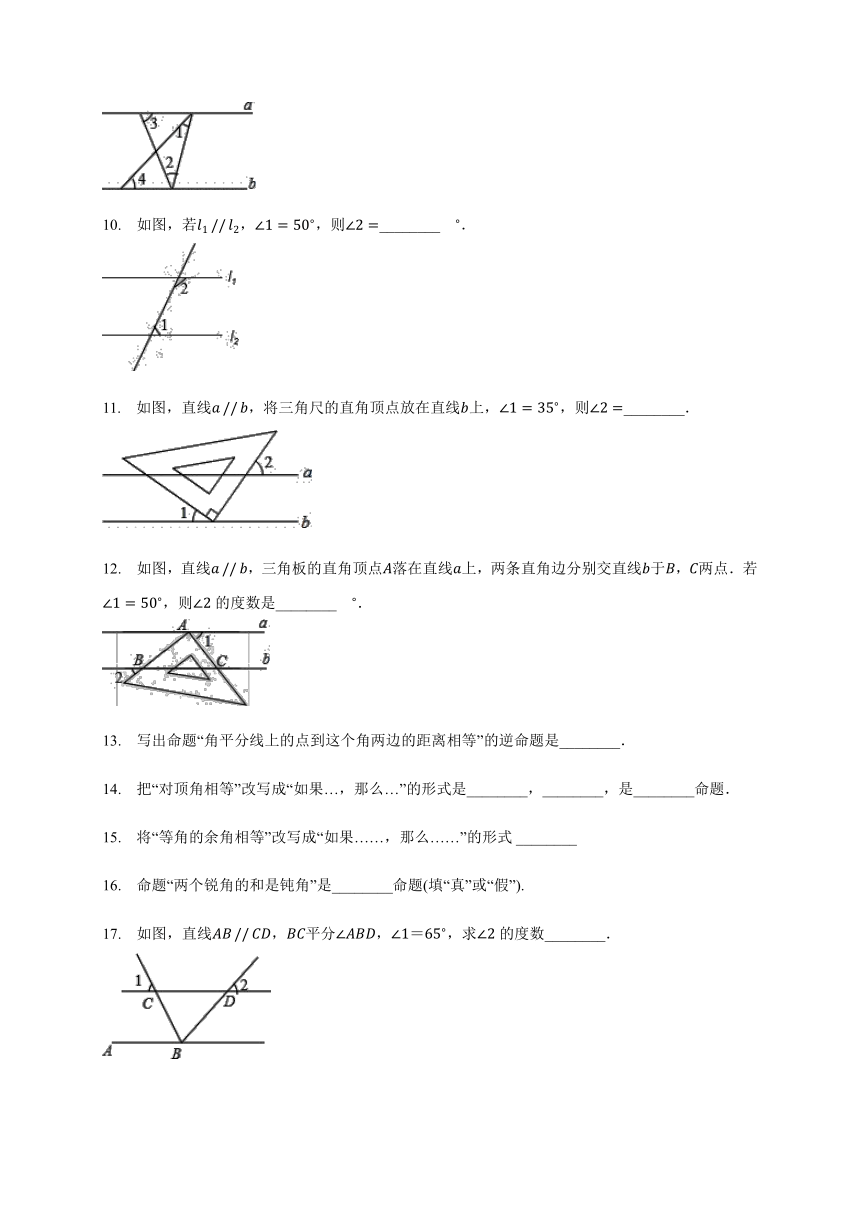
9. 如图,a?//?b,∠1+∠2=70?,则∠3+∠4=________??.
? ?
10. 如图,若l1?//?l2,∠1=50?,则∠2=________??.
? ?
11. 如图,直线a?//?b,将三角尺的直角顶点放在直线b上,∠1=35?,则∠2=________.
?
12. 如图,直线a?//?b,三角板的直角顶点A落在直线a上,两条直角边分别交直线b于B,C两点.若∠1=50?,则∠2的度数是________??.
?
13. 写出命题“角平分线上的点到这个角两边的距离相等”的逆命题是________. ?
14. 把“对顶角相等”改写成“如果…,那么…”的形式是________,________,是________命题. ?
15. 将“等角的余角相等”改写成“如果……,那么……”的形式?________ ?
16. 命题“两个锐角的和是钝角”是________命题(填“真”或“假”). ?
17. 如图,直线AB?//?CD,BC平分∠ABD,∠1=65?,求∠2的度数________.
三、 解答题 (本题共计 7 小题 ,共计69分 ) ?
18. 如图,AB?//?CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论
?
19. 已知如图:AD?//?BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30?.
(1)求证:DC//AB.
(2)求∠AFE的大小
?
20. 如图,已知:AB?//?CD,不添加辅助线,试再添加一个条件,使∠1=∠2成立.
(1)写出两个合适的条件;
(2)选择其中一个加以证明.
?21. 已知:如图,△ABC中,AD⊥BC于点D,点E在AB上,EF⊥BC于点F,∠1=∠2,求证:DE?//?AC.
?
22. 已知AB?//?DE,∠B=60?,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
?
23. 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一条直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE?//?AF.
(1)请你用其中两个关系式作为条件,另一个作为结论,写出一个你认为正确的命题;(用序号写出命题的书写形式,如:如果??,那么?)
(2)说明你写的一个命题的正确性.
?
24. 如图,已知AM?//?BN,∠A=60?.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠________的度数是________;②∵ ________?//?________,∴ ∠________=∠________;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
D
【解答】
解:ABICD,
∠A=∠ADC
ABIIEF,
∴ A=∠AFE
AFCG
EE=∠AFE=E=
:CDIEF,
加EGC=∠DCG=∠A
所以与2A相等的角有∠ADC.∠AFE,∠EGC.2GCD四个,
故选:D
2.
【答案】
D
【解答】
解:如图所示,根据图中直线a、b被c所截形成的内错角相等,可得依据为内错角相等,两直线平行.
故选D
3.
【答案】
D
【解答】
解:A、任何一个命题都有逆命题,所以A选项的说法正确;
B、一个真命题的逆命题可能是真命题,也可能为假命题,所以B选项的说法正确;
C、一个定理不一定有逆定理,所以C选项的说法正确;
D、有的定理有逆定理,有的定理不一定有逆定理,所以D选项的说法错误.
故选D.
4.
【答案】
A
【解答】
解:设取款一次时间为t,根据题意可得出ABCD四种取款相对取款时间及等待时间之和,
则:A、张丽,王云,李玲,张丽取款时间为t,王云等待时间为t、取款时间为2t,李玲等待时间为2t、取款时间为3t,即总时间为:t+t+2t+2t+3t=9t;
B、李玲,张丽,王云,李玲取款时间为3t,张丽等待时间为3t、取款时间为t,王云等待时间为t、取款时间为2t,
即总时间为:3t+3t+t+t+2t=10t;
C、张丽,李玲,王云,张丽取款时间为t,李玲等待时间为t、取款时间为3t,王云等待时间为3t、取款时间为2t,
即总时间为:t+t+3t+3t+2t=10t;
D、王云,李玲,张丽,王云取款时间为2t,李玲等待时间为2t、取款时间为3t,张丽等待时间为3t、取款时间为t,
即总时间为:2t+2t3t+3t+t=11t;
所以按A、张丽,王云,李玲顺序取款才能使三人所花总时间最少(包括等待时间);
故选:A.
5.
【答案】
A
【解答】
解:根据题意,知丙共当裁判8局,所以甲乙之间共有8局比赛,
又甲共打了12局,乙共打了21局,所以甲和丙打了4局,乙和丙打了13局,
三个人之间总共打了(8+4+13)=25局,
考查甲,总共打了12局,当了13次裁判,所以他输了12次.
所以当n是偶数时,第n局比赛的输方为甲,从而整个比赛的第10局的输方必是甲.
故选:A.
6.
【答案】
B
【解答】
解:如图,过点B作BD?//?l,
∵ 直线l?//?m,
∴ BD?//?l?//?m,
∴ ∠3=∠1=20?,
∵ △ABC是有一个角是45?的直角三角板,
∴ ∠4=45?-∠3=45?-24?=25?,
∴ ∠2=∠4=25?.
故选B.
7.
【答案】
C
【解答】
解:A,对角线相等吗?是疑问句,不符合命题的定义,不是命题;
B,作线段AB=10cm,这是作图语言,不符合命题的定义,不是命题;
C,若a=b,则-a=-b符合命题的定义,是命题;
D,连接A,B两点,这是作图语言,不符合命题的定义,不是命题.
故选C.
8.
【答案】
D
【解答】
解:A,求1+2+3+4+5+6的值,不是命题,故A错误;
B,过点P作PC//OA,不是命题,故B错误;
C,能根据等式的性质解方程吗,不是命题,故C错误;
D,房屋顶棚是彩钢做的,是命题,故D正确.
故选D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
9.
【答案】
110
【解答】
解:如图,
∵ a?//?b,
∴ ∠3=∠5.
∵ ∠1+∠2=70?,
∴ ∠6=110?,
∴ ∠3+∠4=∠4+∠5=∠6=110?.
故答案为:110?.
10.
【答案】
130
【解答】
解:∵ l1?//?l2,∠1=50?,
∴ ∠2=180?-∠1=180?-50?=130?,
故答案为:130.
11.
【答案】
55?
【解答】
解:如图,
∵ ∠1=35?,
∴ ∠3=180?-35?-90?=55?,
∵ a?//?b,
∴ ∠2=∠3=55?.
故答案为:55?.
12.
【答案】
40
【解答】
解:如图:
∵ ∠BAC=90?,∠1=50?,
∴ ∠3=90?-∠1=90?-50?=40?.
∵ 直线a?//?b,
∴ ∠2=∠3=40?.
故答案为:40.
13.
【答案】
到角的两边距离相等的点在角平分线上
【解答】
解:命题“角平分线上的点到这个角两边的距离相等”的逆命题是“到角的两边距离相等的点在角平分线上”.
14.
【答案】
如果这两个角是对顶角,那么这两个角相等;,如果这两个角是对顶角,那么这两个角相等;,真.
【解答】
解:“对顶角相等”改写成“如果...,那么...”的形式是“如果这两个角是对顶角,那么这两个角相等”;
这种命题是成立的,故这是真命题.
故答案为:如果这两个角是对顶角,那么这两个角相等;如果这两个角是对顶角,那么这两个角相等;真.
15.
【答案】
如果两个角相等,那么它们的余角也相等;
【解答】
根据命题的特点,可以改写为:“如果两个角相等,那么它们的余角也相等”,
故答案为如果两个角相等,那么它们的余角也相等.
16.
【答案】
假
【解答】
解:两个锐角的和可能是锐角,直角或钝角,
即两个锐角的和是钝角是假命题.
故答案为:假.
17.
【答案】
50?
【解答】
∵ AB?//?CD,
∴ ∠ABC=∠1=65?(两直线平行,同位角相等),
∠ABD+∠BDC=180?(两直线平行,同旁内角互补),
∵ BC平分∠ABD,
∴ ∠ABD=2∠ABC=130?(角平分线定义)
∴ ∠BDC=180?-∠ABD=50?,
∴ ∠2=∠BDC=50?(对顶角相等).
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
18.
【答案】
∠B+∠D=∠BPD.
理由如下:作PQ?//?AB,如图,
∵ AB?//?CD,
∴ AB?//?PQ,
∵ ∠B=∠BPQ,∠D=∠DPQ,
∴ ∠B+∠D=∠BPQ+∠DPQ=∠BPD.
【解答】
∠B+∠D=∠BPD.
理由如下:作PQ?//?AB,如图,
∵ AB?//?CD,
∴ AB?//?PQ,
∵ ∠B=∠BPQ,∠D=∠DPQ,
∴ ∠B+∠D=∠BPQ+∠DPQ=∠BPD.
19.
【答案】
(1)证明见解析,
(2) 60?
【解答】
(1)∵ AD/BCC&
(2):AEE, △AEF=90?,∠DEA=30? ∴ DEF=30?+90?=120??DC/AB
∠DEF+∠F=180? △AFE=60?
20.
【答案】
解:(1)AE?//?FH;∠EAH=∠FHA;∠E=∠F(写出两个即可).
(2)选择:AE?//?FH.
证明:因为AB?//?CD,
所以∠BAH=∠CHA,
又因为AE?//?FH,
所以∠EAH=∠FHA,
所以∠BAH-∠EAH=∠CHA-∠FHA,
即∠1=∠2.
【解答】
解:(1)AE?//?FH;∠EAH=∠FHA;∠E=∠F(写出两个即可).
(2)选择:AE?//?FH.
证明:因为AB?//?CD,
所以∠BAH=∠CHA,
又因为AE?//?FH,
所以∠EAH=∠FHA,
所以∠BAH-∠EAH=∠CHA-∠FHA,
即∠1=∠2.
21.
【答案】
证明:∵ AD⊥BC于点D,EF⊥BC于点F,
∴ AD?//?EF.?
∴ ∠1=∠3.???
∵ ∠1=∠2,
∴ ∠2=∠3.
∴ DE?//?AC.
【解答】
证明:∵ AD⊥BC于点D,EF⊥BC于点F,
∴ AD?//?EF.?
∴ ∠1=∠3.???
∵ ∠1=∠2,
∴ ∠2=∠3.
∴ DE?//?AC.
22.
【答案】
解:∵ AB?//?DE,∠B=60?,
∴ ∠BCD=120?.
∵ CM平分∠DCB,
∴ ∠DCM=12∠DCB=60?.
∵ CM⊥CN,
∴ ∠MCN=90?,
∴ ∠DCM+∠NCE=90?,
∴ ∠NCE=90?-60?=30?.
【解答】
解:∵ AB?//?DE,∠B=60?,
∴ ∠BCD=120?.
∵ CM平分∠DCB,
∴ ∠DCM=12∠DCB=60?.
∵ CM⊥CN,
∴ ∠MCN=90?,
∴ ∠DCM+∠NCE=90?,
∴ ∠NCE=90?-60?=30?.
23.
【答案】
解:(1)如果①,③,那么②;如果②,③,那么①;
(2)对于命题“如果①,③,那么②”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ AD=BC,∠A=∠B,
∴ △ADF?△BCE,
∴ DF=CE.
∴ DF-EF=CE-EF,即DE=CF;
对于命题“如果②,③,那么①”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ DE=CF,
∴ DE+EF=CF+EF,即DF=CE.
∵ ∠A=∠B,
∴ △ADF?△BCE,
∴ AD=BC.
【解答】
解:(1)如果①,③,那么②;如果②,③,那么①;
(2)对于命题“如果①,③,那么②”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ AD=BC,∠A=∠B,
∴ △ADF?△BCE,
∴ DF=CE.
∴ DF-EF=CE-EF,即DE=CF;
对于命题“如果②,③,那么①”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ DE=CF,
∴ DE+EF=CF+EF,即DF=CE.
∵ ∠A=∠B,
∴ △ADF?△BCE,
∴ AD=BC.
24.
【答案】
ABN,120?,AM,BN,ACB,CBN
∵ AM?//?BN,
∴ ∠ABN+∠A=180?,
∴ ∠ABN=180?-60?=120?,
∴ ∠ABP+∠PBN=120?,
∵ BC平分∠ABP,BD平分∠PBN,
∴ ∠ABP=2∠CBP,∠PBN=2∠DBP,
∴ 2∠CBP+2∠DBP=120?,
∴ ∠CBD=∠CBP+∠DBP=60?;
不变,∠APB:∠ADB=2:1.
∵ AM?//?BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
∵ BD平分∠PBN,
∴ ∠PBN=2∠DBN,
∴ ∠APB:∠ADB=2:1.
【解答】
①∵ AM?//?BN,∠A=60?,
∴ ∠A+∠ABN=180?,
∴ ∠ABN=120?;
②∵ AM?//?BN,
∴ ∠ACB=∠CBN,
故答案为:120?,CBN;
∵ AM?//?BN,
∴ ∠ABN+∠A=180?,
∴ ∠ABN=180?-60?=120?,
∴ ∠ABP+∠PBN=120?,
∵ BC平分∠ABP,BD平分∠PBN,
∴ ∠ABP=2∠CBP,∠PBN=2∠DBP,
∴ 2∠CBP+2∠DBP=120?,
∴ ∠CBD=∠CBP+∠DBP=60?;
不变,∠APB:∠ADB=2:1.
∵ AM?//?BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
∵ BD平分∠PBN,
∴ ∠PBN=2∠DBN,
∴ ∠APB:∠ADB=2:1.
班级:_____________姓名:_____________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 ) ?
1. 如图,AB?//?CD?//?EF,AF?//?CG,则图中与∠A(不包括∠A)相等的角有( )
A.1个 B.2个 C.3个 D.4个?
2. 如图所示,过点P画直线a的平行线b的作法的依据是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
?
3. 下列命题中错误的是(? ? ? ? )
A.任何一个命题都有逆命题
B.一个真命题的逆命题可能是真命题
C.一个定理不一定有逆定理
D.任何一个定理都没有逆定理?
4. 师范大学学生张丽、王云、李玲三人一起去银行柜员机取钱,张丽取款一次,王云取款两次,李玲取款三次,假设每取款一次所用时间相同,请问她们三人按什么样的顺序取款,才能使三人所花总时间最少(包括等待时间)( )
A.张丽,王云,李玲 B.李玲,张丽,王云
C.张丽,李玲,王云 D.王云,李玲,张丽
5. 甲、乙、丙三人用擂台赛形式进行训练.每局两人单打比赛,另一人当裁判.每一局输者当下一局的裁判,而原来的裁判与赢者比赛.一天训练结束时,统计甲共打12局,乙共打21局,而丙共当裁判8局.那么整个比赛中第10局的输者( )
A.必是甲 B.必是乙 C.必是丙 D.不能确定
6. 如图,直线l?//?m,将含有45?角的三角形板ABC的直角顶点C放在直线m上,若∠1=20?,则∠2的度数为(? ? ? ? )
A.20? B.25? C.30? D.35??
7. 下列语句是命题的是(? ? ? ? )
A.对角线相等吗? B.作线段AB=10cm
C.若a=b,则-a=-b D.连接A,B 两点
8. 下列句子是命题的是(? ? ? ? )
A.求1+2+3+4+5+6的值 B.过点P作PC//OA
C. 能根据等式的性质解方程吗 D. 房屋顶棚是彩钢做的
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 ) ?
9. 如图,a?//?b,∠1+∠2=70?,则∠3+∠4=________??.
? ?
10. 如图,若l1?//?l2,∠1=50?,则∠2=________??.
? ?
11. 如图,直线a?//?b,将三角尺的直角顶点放在直线b上,∠1=35?,则∠2=________.
?
12. 如图,直线a?//?b,三角板的直角顶点A落在直线a上,两条直角边分别交直线b于B,C两点.若∠1=50?,则∠2的度数是________??.
?
13. 写出命题“角平分线上的点到这个角两边的距离相等”的逆命题是________. ?
14. 把“对顶角相等”改写成“如果…,那么…”的形式是________,________,是________命题. ?
15. 将“等角的余角相等”改写成“如果……,那么……”的形式?________ ?
16. 命题“两个锐角的和是钝角”是________命题(填“真”或“假”). ?
17. 如图,直线AB?//?CD,BC平分∠ABD,∠1=65?,求∠2的度数________.
三、 解答题 (本题共计 7 小题 ,共计69分 ) ?
18. 如图,AB?//?CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论
?
19. 已知如图:AD?//?BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30?.
(1)求证:DC//AB.
(2)求∠AFE的大小
?
20. 如图,已知:AB?//?CD,不添加辅助线,试再添加一个条件,使∠1=∠2成立.
(1)写出两个合适的条件;
(2)选择其中一个加以证明.
?21. 已知:如图,△ABC中,AD⊥BC于点D,点E在AB上,EF⊥BC于点F,∠1=∠2,求证:DE?//?AC.
?
22. 已知AB?//?DE,∠B=60?,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
?
23. 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一条直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE?//?AF.
(1)请你用其中两个关系式作为条件,另一个作为结论,写出一个你认为正确的命题;(用序号写出命题的书写形式,如:如果??,那么?)
(2)说明你写的一个命题的正确性.
?
24. 如图,已知AM?//?BN,∠A=60?.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠________的度数是________;②∵ ________?//?________,∴ ∠________=∠________;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
D
【解答】
解:ABICD,
∠A=∠ADC
ABIIEF,
∴ A=∠AFE
AFCG
EE=∠AFE=E=
:CDIEF,
加EGC=∠DCG=∠A
所以与2A相等的角有∠ADC.∠AFE,∠EGC.2GCD四个,
故选:D
2.
【答案】
D
【解答】
解:如图所示,根据图中直线a、b被c所截形成的内错角相等,可得依据为内错角相等,两直线平行.
故选D
3.
【答案】
D
【解答】
解:A、任何一个命题都有逆命题,所以A选项的说法正确;
B、一个真命题的逆命题可能是真命题,也可能为假命题,所以B选项的说法正确;
C、一个定理不一定有逆定理,所以C选项的说法正确;
D、有的定理有逆定理,有的定理不一定有逆定理,所以D选项的说法错误.
故选D.
4.
【答案】
A
【解答】
解:设取款一次时间为t,根据题意可得出ABCD四种取款相对取款时间及等待时间之和,
则:A、张丽,王云,李玲,张丽取款时间为t,王云等待时间为t、取款时间为2t,李玲等待时间为2t、取款时间为3t,即总时间为:t+t+2t+2t+3t=9t;
B、李玲,张丽,王云,李玲取款时间为3t,张丽等待时间为3t、取款时间为t,王云等待时间为t、取款时间为2t,
即总时间为:3t+3t+t+t+2t=10t;
C、张丽,李玲,王云,张丽取款时间为t,李玲等待时间为t、取款时间为3t,王云等待时间为3t、取款时间为2t,
即总时间为:t+t+3t+3t+2t=10t;
D、王云,李玲,张丽,王云取款时间为2t,李玲等待时间为2t、取款时间为3t,张丽等待时间为3t、取款时间为t,
即总时间为:2t+2t3t+3t+t=11t;
所以按A、张丽,王云,李玲顺序取款才能使三人所花总时间最少(包括等待时间);
故选:A.
5.
【答案】
A
【解答】
解:根据题意,知丙共当裁判8局,所以甲乙之间共有8局比赛,
又甲共打了12局,乙共打了21局,所以甲和丙打了4局,乙和丙打了13局,
三个人之间总共打了(8+4+13)=25局,
考查甲,总共打了12局,当了13次裁判,所以他输了12次.
所以当n是偶数时,第n局比赛的输方为甲,从而整个比赛的第10局的输方必是甲.
故选:A.
6.
【答案】
B
【解答】
解:如图,过点B作BD?//?l,
∵ 直线l?//?m,
∴ BD?//?l?//?m,
∴ ∠3=∠1=20?,
∵ △ABC是有一个角是45?的直角三角板,
∴ ∠4=45?-∠3=45?-24?=25?,
∴ ∠2=∠4=25?.
故选B.
7.
【答案】
C
【解答】
解:A,对角线相等吗?是疑问句,不符合命题的定义,不是命题;
B,作线段AB=10cm,这是作图语言,不符合命题的定义,不是命题;
C,若a=b,则-a=-b符合命题的定义,是命题;
D,连接A,B两点,这是作图语言,不符合命题的定义,不是命题.
故选C.
8.
【答案】
D
【解答】
解:A,求1+2+3+4+5+6的值,不是命题,故A错误;
B,过点P作PC//OA,不是命题,故B错误;
C,能根据等式的性质解方程吗,不是命题,故C错误;
D,房屋顶棚是彩钢做的,是命题,故D正确.
故选D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
9.
【答案】
110
【解答】
解:如图,
∵ a?//?b,
∴ ∠3=∠5.
∵ ∠1+∠2=70?,
∴ ∠6=110?,
∴ ∠3+∠4=∠4+∠5=∠6=110?.
故答案为:110?.
10.
【答案】
130
【解答】
解:∵ l1?//?l2,∠1=50?,
∴ ∠2=180?-∠1=180?-50?=130?,
故答案为:130.
11.
【答案】
55?
【解答】
解:如图,
∵ ∠1=35?,
∴ ∠3=180?-35?-90?=55?,
∵ a?//?b,
∴ ∠2=∠3=55?.
故答案为:55?.
12.
【答案】
40
【解答】
解:如图:
∵ ∠BAC=90?,∠1=50?,
∴ ∠3=90?-∠1=90?-50?=40?.
∵ 直线a?//?b,
∴ ∠2=∠3=40?.
故答案为:40.
13.
【答案】
到角的两边距离相等的点在角平分线上
【解答】
解:命题“角平分线上的点到这个角两边的距离相等”的逆命题是“到角的两边距离相等的点在角平分线上”.
14.
【答案】
如果这两个角是对顶角,那么这两个角相等;,如果这两个角是对顶角,那么这两个角相等;,真.
【解答】
解:“对顶角相等”改写成“如果...,那么...”的形式是“如果这两个角是对顶角,那么这两个角相等”;
这种命题是成立的,故这是真命题.
故答案为:如果这两个角是对顶角,那么这两个角相等;如果这两个角是对顶角,那么这两个角相等;真.
15.
【答案】
如果两个角相等,那么它们的余角也相等;
【解答】
根据命题的特点,可以改写为:“如果两个角相等,那么它们的余角也相等”,
故答案为如果两个角相等,那么它们的余角也相等.
16.
【答案】
假
【解答】
解:两个锐角的和可能是锐角,直角或钝角,
即两个锐角的和是钝角是假命题.
故答案为:假.
17.
【答案】
50?
【解答】
∵ AB?//?CD,
∴ ∠ABC=∠1=65?(两直线平行,同位角相等),
∠ABD+∠BDC=180?(两直线平行,同旁内角互补),
∵ BC平分∠ABD,
∴ ∠ABD=2∠ABC=130?(角平分线定义)
∴ ∠BDC=180?-∠ABD=50?,
∴ ∠2=∠BDC=50?(对顶角相等).
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
18.
【答案】
∠B+∠D=∠BPD.
理由如下:作PQ?//?AB,如图,
∵ AB?//?CD,
∴ AB?//?PQ,
∵ ∠B=∠BPQ,∠D=∠DPQ,
∴ ∠B+∠D=∠BPQ+∠DPQ=∠BPD.
【解答】
∠B+∠D=∠BPD.
理由如下:作PQ?//?AB,如图,
∵ AB?//?CD,
∴ AB?//?PQ,
∵ ∠B=∠BPQ,∠D=∠DPQ,
∴ ∠B+∠D=∠BPQ+∠DPQ=∠BPD.
19.
【答案】
(1)证明见解析,
(2) 60?
【解答】
(1)∵ AD/BCC&
(2):AEE, △AEF=90?,∠DEA=30? ∴ DEF=30?+90?=120??DC/AB
∠DEF+∠F=180? △AFE=60?
20.
【答案】
解:(1)AE?//?FH;∠EAH=∠FHA;∠E=∠F(写出两个即可).
(2)选择:AE?//?FH.
证明:因为AB?//?CD,
所以∠BAH=∠CHA,
又因为AE?//?FH,
所以∠EAH=∠FHA,
所以∠BAH-∠EAH=∠CHA-∠FHA,
即∠1=∠2.
【解答】
解:(1)AE?//?FH;∠EAH=∠FHA;∠E=∠F(写出两个即可).
(2)选择:AE?//?FH.
证明:因为AB?//?CD,
所以∠BAH=∠CHA,
又因为AE?//?FH,
所以∠EAH=∠FHA,
所以∠BAH-∠EAH=∠CHA-∠FHA,
即∠1=∠2.
21.
【答案】
证明:∵ AD⊥BC于点D,EF⊥BC于点F,
∴ AD?//?EF.?
∴ ∠1=∠3.???
∵ ∠1=∠2,
∴ ∠2=∠3.
∴ DE?//?AC.
【解答】
证明:∵ AD⊥BC于点D,EF⊥BC于点F,
∴ AD?//?EF.?
∴ ∠1=∠3.???
∵ ∠1=∠2,
∴ ∠2=∠3.
∴ DE?//?AC.
22.
【答案】
解:∵ AB?//?DE,∠B=60?,
∴ ∠BCD=120?.
∵ CM平分∠DCB,
∴ ∠DCM=12∠DCB=60?.
∵ CM⊥CN,
∴ ∠MCN=90?,
∴ ∠DCM+∠NCE=90?,
∴ ∠NCE=90?-60?=30?.
【解答】
解:∵ AB?//?DE,∠B=60?,
∴ ∠BCD=120?.
∵ CM平分∠DCB,
∴ ∠DCM=12∠DCB=60?.
∵ CM⊥CN,
∴ ∠MCN=90?,
∴ ∠DCM+∠NCE=90?,
∴ ∠NCE=90?-60?=30?.
23.
【答案】
解:(1)如果①,③,那么②;如果②,③,那么①;
(2)对于命题“如果①,③,那么②”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ AD=BC,∠A=∠B,
∴ △ADF?△BCE,
∴ DF=CE.
∴ DF-EF=CE-EF,即DE=CF;
对于命题“如果②,③,那么①”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ DE=CF,
∴ DE+EF=CF+EF,即DF=CE.
∵ ∠A=∠B,
∴ △ADF?△BCE,
∴ AD=BC.
【解答】
解:(1)如果①,③,那么②;如果②,③,那么①;
(2)对于命题“如果①,③,那么②”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ AD=BC,∠A=∠B,
∴ △ADF?△BCE,
∴ DF=CE.
∴ DF-EF=CE-EF,即DE=CF;
对于命题“如果②,③,那么①”证明如下:
∵ BE?//?AF,
∴ ∠AFD=∠BEC.
∵ DE=CF,
∴ DE+EF=CF+EF,即DF=CE.
∵ ∠A=∠B,
∴ △ADF?△BCE,
∴ AD=BC.
24.
【答案】
ABN,120?,AM,BN,ACB,CBN
∵ AM?//?BN,
∴ ∠ABN+∠A=180?,
∴ ∠ABN=180?-60?=120?,
∴ ∠ABP+∠PBN=120?,
∵ BC平分∠ABP,BD平分∠PBN,
∴ ∠ABP=2∠CBP,∠PBN=2∠DBP,
∴ 2∠CBP+2∠DBP=120?,
∴ ∠CBD=∠CBP+∠DBP=60?;
不变,∠APB:∠ADB=2:1.
∵ AM?//?BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
∵ BD平分∠PBN,
∴ ∠PBN=2∠DBN,
∴ ∠APB:∠ADB=2:1.
【解答】
①∵ AM?//?BN,∠A=60?,
∴ ∠A+∠ABN=180?,
∴ ∠ABN=120?;
②∵ AM?//?BN,
∴ ∠ACB=∠CBN,
故答案为:120?,CBN;
∵ AM?//?BN,
∴ ∠ABN+∠A=180?,
∴ ∠ABN=180?-60?=120?,
∴ ∠ABP+∠PBN=120?,
∵ BC平分∠ABP,BD平分∠PBN,
∴ ∠ABP=2∠CBP,∠PBN=2∠DBP,
∴ 2∠CBP+2∠DBP=120?,
∴ ∠CBD=∠CBP+∠DBP=60?;
不变,∠APB:∠ADB=2:1.
∵ AM?//?BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
∵ BD平分∠PBN,
∴ ∠PBN=2∠DBN,
∴ ∠APB:∠ADB=2:1.
