北师大版(2012)七年级下册数学随堂小练 6.2频率的稳定性(Word版 有答案)
文档属性
| 名称 | 北师大版(2012)七年级下册数学随堂小练 6.2频率的稳定性(Word版 有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 09:51:25 | ||
图片预览


文档简介
数学随堂小练北师大版(2012)七年级下册
6.2频率的稳定性
一、单选题
1.某小组做“用频率估计概率”的试验时,绘出了如图所示的频率折线图,则符合这一结果的试验可能是( )
A.抛掷一枚硬币,出现正面
B.掷一枚正六面体骰子,向上一面的点数是3
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球
2.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( )
A.12个B.24个C.36个D.48个
3.下列说法正确的是( )
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”“两个反面”“一正一反”的机会相同。
A.①② B.②③ C.③④ D.①③
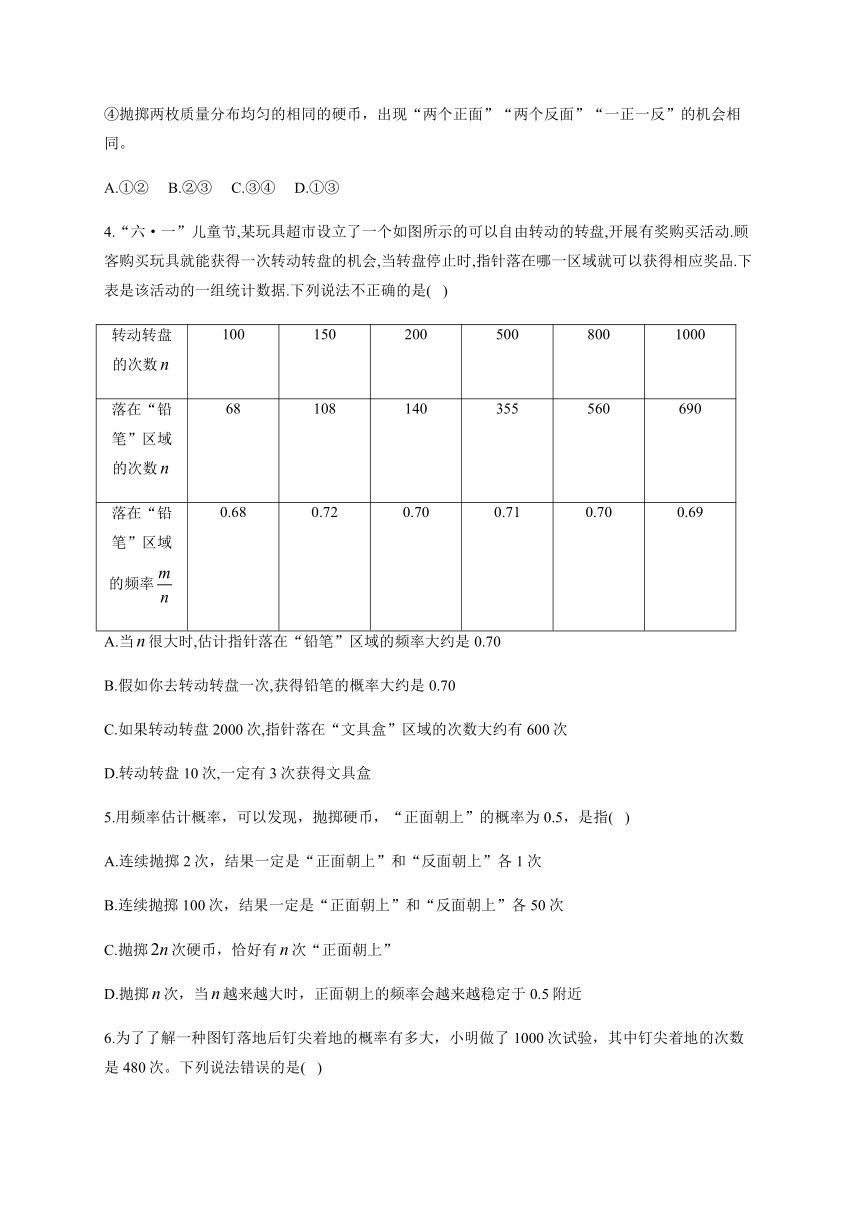
4.“六·一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
转动转盘的次数false
100
150
200
500
800
1000
落在“铅笔”区域的次数false
68
108
140
355
560
690
落在“铅笔”区域的频率false
0.68
0.72
0.70
0.71
0.70
0.69
A.当false很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
5.用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷false次硬币,恰好有false次“正面朝上”
D.抛掷false次,当false越来越大时,正面朝上的频率会越来越稳定于0.5附近
6.为了了解一种图钉落地后钉尖着地的概率有多大,小明做了1000次试验,其中钉尖着地的次数是480次。下列说法错误的是( )
A.钉尖着地的频率是0.48
B.前500次试验结束后,钉尖着地的次数一定是240次
C.钉尖着地的概率大约是0.48
D.随着试验次数的增加,钉尖着地的频率稳定在0.48附近
7.下列说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%
B.抛掷一枚普通的正六面体般子,出现6点朝上的概率是false的意思是每掷6次就有1次掷得6点朝上
C.某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
8.如图显示了用计算机模拟随机抛掷一枚图钉的某次试验的结果.下面有3个推断:①当投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0. 618;③若再次用计算机模拟试验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是(???)
A.① B.② C. ①② D. ①③
9.在相同条件下对某种小麦种子做发芽试验.结果如下表所示.由表估计该麦种的发芽概率是( )
试验粒数n
50
200
500
1000
3000
发芽粒数m
45
188
476
951
2850
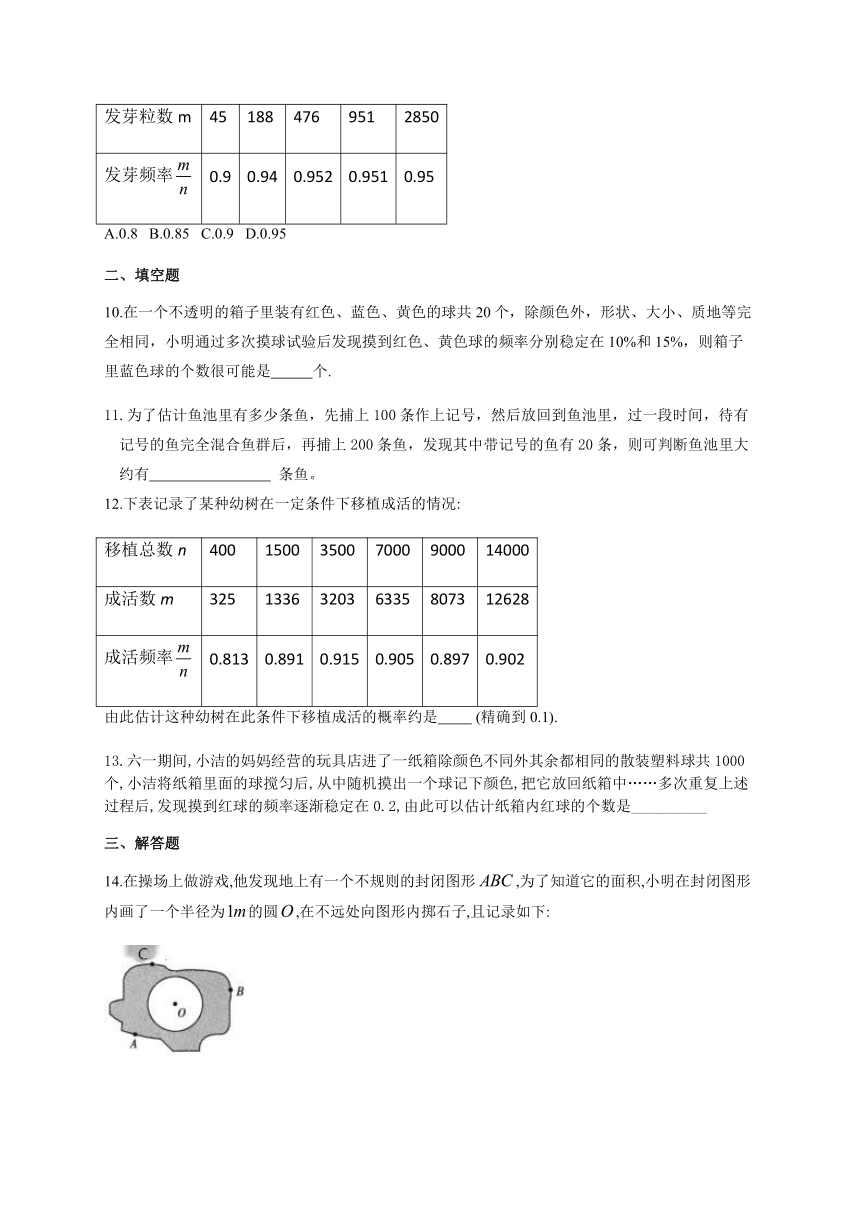
发芽频率false
0.9
0.94
0.952
0.951
0.95
A.0.8 B.0.85 C.0.9 D.0.95
二、填空题
10.在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球试验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 个.
11.为了估计鱼池里有多少条鱼,先捕上100条作上记号,然后放回到鱼池里,过一段时间,待有记号的鱼完全混合鱼群后,再捕上200条鱼,发现其中带记号的鱼有20条,则可判断鱼池里大约有 条鱼。
12.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n
400
1500
3500
7000
9000
14000
成活数m
325
1336
3203
6335
8073
12628
成活频率false
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是 (精确到0.1).
13.六一期间,小洁的妈妈经营的玩具店进了一纸箱除颜色不同外其余都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下颜色,把它放回纸箱中……多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数是__________
三、解答题
14.在操场上做游戏,他发现地上有一个不规则的封闭图形false,为了知道它的面积,小明在封闭图形内画了一个半径为false的圆false,在不远处向图形内掷石子,且记录如下:
掷石子次数
50次
150次
300次
500次
1000次
石子落在圆false (含圆上)的次数false
14
43
93
152
326
石子落在封闭图形false内的次数false
29
85
186
300
650
1.请估算false的值(精确到false);
2.请估算出封闭图形false的面积。
参考答案
1.答案:D
A.抛掷一枚硬币,出现正面朝上的频率趋近于false,不符合题意;
B掷一枚正六面体骰子,向上一面的点数是3的频率为=0.17,不符合题意;
C.一副去掉大小王的普通扑克牌13洗匀后,从中任抽一张牌的花色是红桃的频率趋近于false,不符合题意;
D.从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球的频率趋近于false,符合题意故选D.
2.答案:B
false小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,
false估计摸到红色、黑色球的概率分别为0.15和0.45,
false摸到白球的概率为false,
false口袋中白色球的个数很可能为false(个)。
3.答案:B
试验条件会极大地影响某事件出现的频率,①错误;出现“两个正面”“两个反面”的概率均为false,“一正一反”的概率为false,④错误.②③正确。
4.答案:D
选项A,频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70.由选项A可知选项B,转动转盘一次,获得铅笔的概率大约是0.70。选项C,指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有false(次),选项D是随机事件,结果不确定。
5.答案:D
连续抛掷false次,正面朝上和反面朝上的次数不一定各一半,故A,B,C错误;抛掷false次,当false越来越大时,正面朝上的频率会越来越稳定于0.5附近,D正确.
6.答案:B
前500次试验结束后,钉尖着地的次数不一定是240次,故选B.
7.答案:D
A、10次抛图钉的试验太少,错误;
B、概率是反映事件发生机会的大小的概念,机会大也不一定发生,错误;
C、概率是反映事件发生机会的大小的概念,机会大也不一定发生,错误;
D、根据概率的统计定义,可知正确.故选D.
8.答案:B
当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以此时“钉尖向上”的可能性是:false,但“钉尖向上”的概率不一定是0.616,故①错误,
随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618,故②正确,
若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故③错误,故选:B
9.答案:D
false种子粒数3000粒时,种子发芽的频率趋近于0.95,
false估计种子发芽的概率为0.95.
10.答案:15
根据题意得摸到红色、黄色球的概率为10%和15%,
所以摸到蓝球的概率为75%,
因为false (个),
所以可估计袋中蓝色球的个数为15个.
故答案为15.
11.答案:1000
根据题意得:
false (条)
答:鱼池里大约有1000条鱼;
故答案为:1000.
12.答案:0.9
概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率
false这种幼树移植成活率的概率约为0.9.
故答案为:0.9.
13.答案:200
因为摸到红球的频率在0.2附近波动,所以摸出红球的概率为0.2,再设出红球的个数,根据概率公式列方程解答即可.
试题解析:设红球的个数为x,
∵红球的频率在0.2附近波动,
∴摸出红球的概率为0.2,即
false,
解得false.
所以可以估计红球的个数为200.
考点:利用频率估计概率.
14.答案:1. falsefalse
∴false的值稳定在false附近,即false。
2.设封闭图形false的面积为false,则false∴falsefalse.
6.2频率的稳定性
一、单选题
1.某小组做“用频率估计概率”的试验时,绘出了如图所示的频率折线图,则符合这一结果的试验可能是( )
A.抛掷一枚硬币,出现正面
B.掷一枚正六面体骰子,向上一面的点数是3
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球
2.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( )
A.12个B.24个C.36个D.48个
3.下列说法正确的是( )
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”“两个反面”“一正一反”的机会相同。
A.①② B.②③ C.③④ D.①③
4.“六·一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
转动转盘的次数false
100
150
200
500
800
1000
落在“铅笔”区域的次数false
68
108
140
355
560
690
落在“铅笔”区域的频率false
0.68
0.72
0.70
0.71
0.70
0.69
A.当false很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
5.用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷false次硬币,恰好有false次“正面朝上”
D.抛掷false次,当false越来越大时,正面朝上的频率会越来越稳定于0.5附近
6.为了了解一种图钉落地后钉尖着地的概率有多大,小明做了1000次试验,其中钉尖着地的次数是480次。下列说法错误的是( )
A.钉尖着地的频率是0.48
B.前500次试验结束后,钉尖着地的次数一定是240次
C.钉尖着地的概率大约是0.48
D.随着试验次数的增加,钉尖着地的频率稳定在0.48附近
7.下列说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%
B.抛掷一枚普通的正六面体般子,出现6点朝上的概率是false的意思是每掷6次就有1次掷得6点朝上
C.某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
8.如图显示了用计算机模拟随机抛掷一枚图钉的某次试验的结果.下面有3个推断:①当投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0. 618;③若再次用计算机模拟试验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是(???)
A.① B.② C. ①② D. ①③
9.在相同条件下对某种小麦种子做发芽试验.结果如下表所示.由表估计该麦种的发芽概率是( )
试验粒数n
50
200
500
1000
3000
发芽粒数m
45
188
476
951
2850
发芽频率false
0.9
0.94
0.952
0.951
0.95
A.0.8 B.0.85 C.0.9 D.0.95
二、填空题
10.在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球试验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 个.
11.为了估计鱼池里有多少条鱼,先捕上100条作上记号,然后放回到鱼池里,过一段时间,待有记号的鱼完全混合鱼群后,再捕上200条鱼,发现其中带记号的鱼有20条,则可判断鱼池里大约有 条鱼。
12.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n
400
1500
3500
7000
9000
14000
成活数m
325
1336
3203
6335
8073
12628
成活频率false
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是 (精确到0.1).
13.六一期间,小洁的妈妈经营的玩具店进了一纸箱除颜色不同外其余都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下颜色,把它放回纸箱中……多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数是__________
三、解答题
14.在操场上做游戏,他发现地上有一个不规则的封闭图形false,为了知道它的面积,小明在封闭图形内画了一个半径为false的圆false,在不远处向图形内掷石子,且记录如下:
掷石子次数
50次
150次
300次
500次
1000次
石子落在圆false (含圆上)的次数false
14
43
93
152
326
石子落在封闭图形false内的次数false
29
85
186
300
650
1.请估算false的值(精确到false);
2.请估算出封闭图形false的面积。
参考答案
1.答案:D
A.抛掷一枚硬币,出现正面朝上的频率趋近于false,不符合题意;
B掷一枚正六面体骰子,向上一面的点数是3的频率为=0.17,不符合题意;
C.一副去掉大小王的普通扑克牌13洗匀后,从中任抽一张牌的花色是红桃的频率趋近于false,不符合题意;
D.从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球的频率趋近于false,符合题意故选D.
2.答案:B
false小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,
false估计摸到红色、黑色球的概率分别为0.15和0.45,
false摸到白球的概率为false,
false口袋中白色球的个数很可能为false(个)。
3.答案:B
试验条件会极大地影响某事件出现的频率,①错误;出现“两个正面”“两个反面”的概率均为false,“一正一反”的概率为false,④错误.②③正确。
4.答案:D
选项A,频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70.由选项A可知选项B,转动转盘一次,获得铅笔的概率大约是0.70。选项C,指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有false(次),选项D是随机事件,结果不确定。
5.答案:D
连续抛掷false次,正面朝上和反面朝上的次数不一定各一半,故A,B,C错误;抛掷false次,当false越来越大时,正面朝上的频率会越来越稳定于0.5附近,D正确.
6.答案:B
前500次试验结束后,钉尖着地的次数不一定是240次,故选B.
7.答案:D
A、10次抛图钉的试验太少,错误;
B、概率是反映事件发生机会的大小的概念,机会大也不一定发生,错误;
C、概率是反映事件发生机会的大小的概念,机会大也不一定发生,错误;
D、根据概率的统计定义,可知正确.故选D.
8.答案:B
当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以此时“钉尖向上”的可能性是:false,但“钉尖向上”的概率不一定是0.616,故①错误,
随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618,故②正确,
若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故③错误,故选:B
9.答案:D
false种子粒数3000粒时,种子发芽的频率趋近于0.95,
false估计种子发芽的概率为0.95.
10.答案:15
根据题意得摸到红色、黄色球的概率为10%和15%,
所以摸到蓝球的概率为75%,
因为false (个),
所以可估计袋中蓝色球的个数为15个.
故答案为15.
11.答案:1000
根据题意得:
false (条)
答:鱼池里大约有1000条鱼;
故答案为:1000.
12.答案:0.9
概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率
false这种幼树移植成活率的概率约为0.9.
故答案为:0.9.
13.答案:200
因为摸到红球的频率在0.2附近波动,所以摸出红球的概率为0.2,再设出红球的个数,根据概率公式列方程解答即可.
试题解析:设红球的个数为x,
∵红球的频率在0.2附近波动,
∴摸出红球的概率为0.2,即
false,
解得false.
所以可以估计红球的个数为200.
考点:利用频率估计概率.
14.答案:1. falsefalse
∴false的值稳定在false附近,即false。
2.设封闭图形false的面积为false,则false∴falsefalse.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
