人教高中数学选修2-3第二章2.3.2离散型随机变量的方差 课件(17张ppt)
文档属性
| 名称 | 人教高中数学选修2-3第二章2.3.2离散型随机变量的方差 课件(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 793.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
2.3.2离散性
随机变量的方差
温故而知新
1、离散型随机变量
X
的均值(数学期望)
2、均值的性质
3、两种特殊分布的均值
(1)若随机变量X服从两点分布,则
(2)若
,则
反映了离散型随机变量取值的平均水平.
二、探究
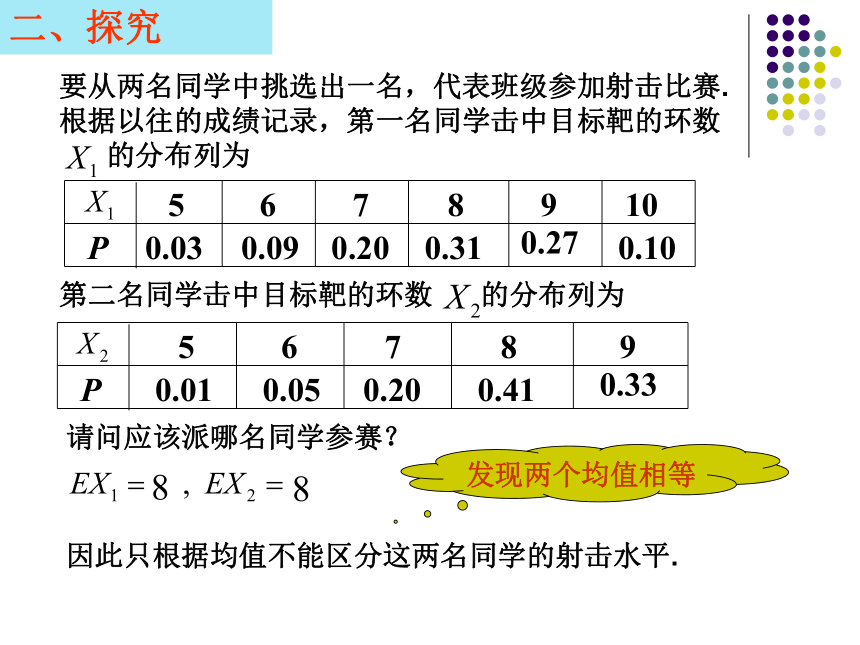
要从两名同学中挑选出一名,代表班级参加射击比赛.
根据以往的成绩记录,第一名同学击中目标靶的环数
的分布列为
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
第二名同学击中目标靶的环数
的分布列为
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
请问应该派哪名同学参赛?
发现两个均值相等
因此只根据均值不能区分这两名同学的射击水平.
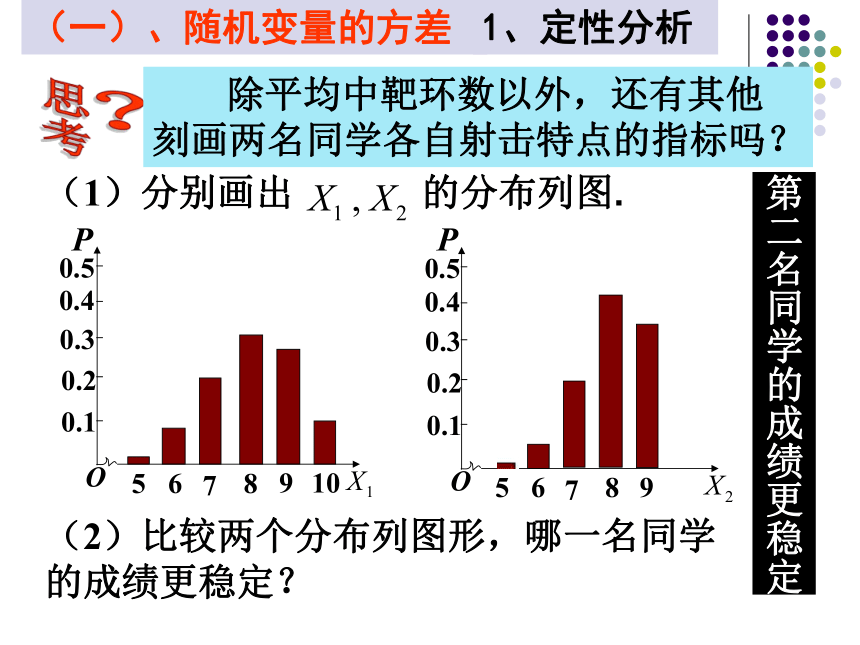
(一)、随机变量的方差
(1)分别画出
的分布列图.
O
5
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
5
6
7
9
8
P
0.1
0.2
0.3
0.4
0.5
(2)比较两个分布列图形,哪一名同学
的成绩更稳定?
除平均中靶环数以外,还有其他
刻画两名同学各自射击特点的指标吗?
1、定性分析
第二名同学的成绩更稳定
2、定量分析
怎样定量刻画随机变量的稳定性?
样本的稳定性是用哪个量刻画的?
方差
方差反映了这组数据的波动情况
在一组数:x1,x2
,…,xn
中,各数据的平均数为
,则这组数据的方差为:
类似于这个概念,我们可以定义随机变量的方差
复习
离散型随机变量取值的方差和标准差:
则称
为随机变量x的方差.
一般地,若离散型随机变量x的概率分布列为:
···
···
···
···
称
为随机变量x的标准差.
定义
3、对方差的几点说明
(1)随机变量的方差和标准差都反映了随机
变量取值偏离于均值的平均程度.方差或标准差
越小,则随机变量偏离于均值的平均程度越小.
(2)随机变量的方差与样本的方差有何联系与区别?
随机变量的方差是常数,而样本的方差是随
着样本的不同而变化的,因此样本的方差是
随机变量.
对于简单随机样本,随着样本容量的增加,
样本方差越来越接近总体方差,因此常用样
本方差来估计总体方差.
1.
已知随机变量x的分布列
x
0
1
2
3
4
P
0.1
0.2
0.4
0.2
0.1
求Dx和σx.
解:
2.
若随机变量x
满足P(x=c)=1,其中c为常数,求Ex
和
Dx.
Ex=c×1=c
Dx=(c-c)2×1=0
练习
结论1:
则
;
结论2:若ξ~B(n,p),则Eξ=
np.
结论
(3)若
ξ
服从两点分布,则
结论3:若
ξ服从两点分布,则
1.已知随机变量x的分布列,则Ex与Dx的值为(
)
(A)
0.6和0.7
(B)1.7和0.3
(C)
0.3和0.7
(D)1.7和0.21
2.已知x~B(100,0.5),则Ex=___,Dx=____,
σx=___.
E(2x-1)=____,
D(2x-1)=____,
σ(2x-1)=_____
x
1
2
P
0.3
0.7
D
50
25
5
99
100
10
3、有一批数量很大的商品,其中次品占1%,现从中任意地连续取出200件商品,设其次品数为X,求EX和DX.
2,1.98
练习
4.若随机变量?服从二项分布,且E?=6,
D
?=4,则此二项分布是
。
设二项分布为?
~B(n,p)
,则
E?=np=6
D?=np(1-p)=4
n=18
p=1/3
试比较两名射手的射击水平.如果其他对手的射击成绩都在8环左右,应派哪一名选手参赛?如果其他对手的射击成绩都在9环左右,应派哪一名选手参赛?
例1、已知甲、乙两名射手在同一条件下射击,所得环数x1、x2的分布列如下:
x1
8
9
10
P
0.2
0.6
0.2
x2
8
9
10
P
0.4
0.2
0.4
如果对手在8环左右,派甲.
如果对手在9环左右,派乙.
例2.随机抛掷一枚质地均匀的骰子,求
向上一面的点数的均值、方差和标准差.
解:抛掷散子所得点数X
的分布列为
P
6
5
4
3
2
1
X
从而
;
.
还有解法不?
例3:有甲乙两个单位都愿意聘用你,而你能
获得如下信息:
甲单位不同职位月工资X1/元
1200
1400
1600
1800
获得相应职位的概率P1
0.4
0.3
0.2
0.1
乙单位不同职位月工资X2/元
1000
1400
1800
2200
获得相应职位的概率P2
0.4
0.3
0.2
0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
解:
因为
,所以两家单位的工资均值相等,但甲单位不同职位的工资相对集中,乙单位不同职位的工资相对分散.这样,如果你希望不同职位的工资差距小一些,就选择甲单位;如果你希望不同职位的工资差距大一些,就选择乙单位.
小结
2、求离散型随机变量X的方差、标准差的一般步骤:
④根据方差、标准差的定义求出
①理解X
的意义,写出X
可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出
EX;
1、熟记方差计算公式
5、对于两个随机变量
和
在
与
相等或很接近时,比较
和
,可以确定哪个随
机变量的性质更适合生产生活实际,适合人们
的需要.
4、掌握方差的线性变化性质
3、能熟练地直接运用两个特殊分布的
方差公式
(1)若
X
服从两点分布,则
(2)若
,则
2.3.2离散性
随机变量的方差
温故而知新
1、离散型随机变量
X
的均值(数学期望)
2、均值的性质
3、两种特殊分布的均值
(1)若随机变量X服从两点分布,则
(2)若
,则
反映了离散型随机变量取值的平均水平.
二、探究
要从两名同学中挑选出一名,代表班级参加射击比赛.
根据以往的成绩记录,第一名同学击中目标靶的环数
的分布列为
P
5
6
7
8
9
10
0.03
0.09
0.20
0.31
0.27
0.10
第二名同学击中目标靶的环数
的分布列为
P
5
6
7
8
9
0.01
0.05
0.20
0.41
0.33
请问应该派哪名同学参赛?
发现两个均值相等
因此只根据均值不能区分这两名同学的射击水平.
(一)、随机变量的方差
(1)分别画出
的分布列图.
O
5
6
7
10
9
8
P
0.1
0.2
0.3
0.4
0.5
O
5
6
7
9
8
P
0.1
0.2
0.3
0.4
0.5
(2)比较两个分布列图形,哪一名同学
的成绩更稳定?
除平均中靶环数以外,还有其他
刻画两名同学各自射击特点的指标吗?
1、定性分析
第二名同学的成绩更稳定
2、定量分析
怎样定量刻画随机变量的稳定性?
样本的稳定性是用哪个量刻画的?
方差
方差反映了这组数据的波动情况
在一组数:x1,x2
,…,xn
中,各数据的平均数为
,则这组数据的方差为:
类似于这个概念,我们可以定义随机变量的方差
复习
离散型随机变量取值的方差和标准差:
则称
为随机变量x的方差.
一般地,若离散型随机变量x的概率分布列为:
···
···
···
···
称
为随机变量x的标准差.
定义
3、对方差的几点说明
(1)随机变量的方差和标准差都反映了随机
变量取值偏离于均值的平均程度.方差或标准差
越小,则随机变量偏离于均值的平均程度越小.
(2)随机变量的方差与样本的方差有何联系与区别?
随机变量的方差是常数,而样本的方差是随
着样本的不同而变化的,因此样本的方差是
随机变量.
对于简单随机样本,随着样本容量的增加,
样本方差越来越接近总体方差,因此常用样
本方差来估计总体方差.
1.
已知随机变量x的分布列
x
0
1
2
3
4
P
0.1
0.2
0.4
0.2
0.1
求Dx和σx.
解:
2.
若随机变量x
满足P(x=c)=1,其中c为常数,求Ex
和
Dx.
Ex=c×1=c
Dx=(c-c)2×1=0
练习
结论1:
则
;
结论2:若ξ~B(n,p),则Eξ=
np.
结论
(3)若
ξ
服从两点分布,则
结论3:若
ξ服从两点分布,则
1.已知随机变量x的分布列,则Ex与Dx的值为(
)
(A)
0.6和0.7
(B)1.7和0.3
(C)
0.3和0.7
(D)1.7和0.21
2.已知x~B(100,0.5),则Ex=___,Dx=____,
σx=___.
E(2x-1)=____,
D(2x-1)=____,
σ(2x-1)=_____
x
1
2
P
0.3
0.7
D
50
25
5
99
100
10
3、有一批数量很大的商品,其中次品占1%,现从中任意地连续取出200件商品,设其次品数为X,求EX和DX.
2,1.98
练习
4.若随机变量?服从二项分布,且E?=6,
D
?=4,则此二项分布是
。
设二项分布为?
~B(n,p)
,则
E?=np=6
D?=np(1-p)=4
n=18
p=1/3
试比较两名射手的射击水平.如果其他对手的射击成绩都在8环左右,应派哪一名选手参赛?如果其他对手的射击成绩都在9环左右,应派哪一名选手参赛?
例1、已知甲、乙两名射手在同一条件下射击,所得环数x1、x2的分布列如下:
x1
8
9
10
P
0.2
0.6
0.2
x2
8
9
10
P
0.4
0.2
0.4
如果对手在8环左右,派甲.
如果对手在9环左右,派乙.
例2.随机抛掷一枚质地均匀的骰子,求
向上一面的点数的均值、方差和标准差.
解:抛掷散子所得点数X
的分布列为
P
6
5
4
3
2
1
X
从而
;
.
还有解法不?
例3:有甲乙两个单位都愿意聘用你,而你能
获得如下信息:
甲单位不同职位月工资X1/元
1200
1400
1600
1800
获得相应职位的概率P1
0.4
0.3
0.2
0.1
乙单位不同职位月工资X2/元
1000
1400
1800
2200
获得相应职位的概率P2
0.4
0.3
0.2
0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
解:
因为
,所以两家单位的工资均值相等,但甲单位不同职位的工资相对集中,乙单位不同职位的工资相对分散.这样,如果你希望不同职位的工资差距小一些,就选择甲单位;如果你希望不同职位的工资差距大一些,就选择乙单位.
小结
2、求离散型随机变量X的方差、标准差的一般步骤:
④根据方差、标准差的定义求出
①理解X
的意义,写出X
可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出
EX;
1、熟记方差计算公式
5、对于两个随机变量
和
在
与
相等或很接近时,比较
和
,可以确定哪个随
机变量的性质更适合生产生活实际,适合人们
的需要.
4、掌握方差的线性变化性质
3、能熟练地直接运用两个特殊分布的
方差公式
(1)若
X
服从两点分布,则
(2)若
,则
