必修3 第三章 概率 3.4概率的应用课时训练(word版含解析)
文档属性
| 名称 | 必修3 第三章 概率 3.4概率的应用课时训练(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 21:37:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
必修3 第三章 概率 3.4概率的应用课时训练
学校:___________姓名:___________
一、选择题
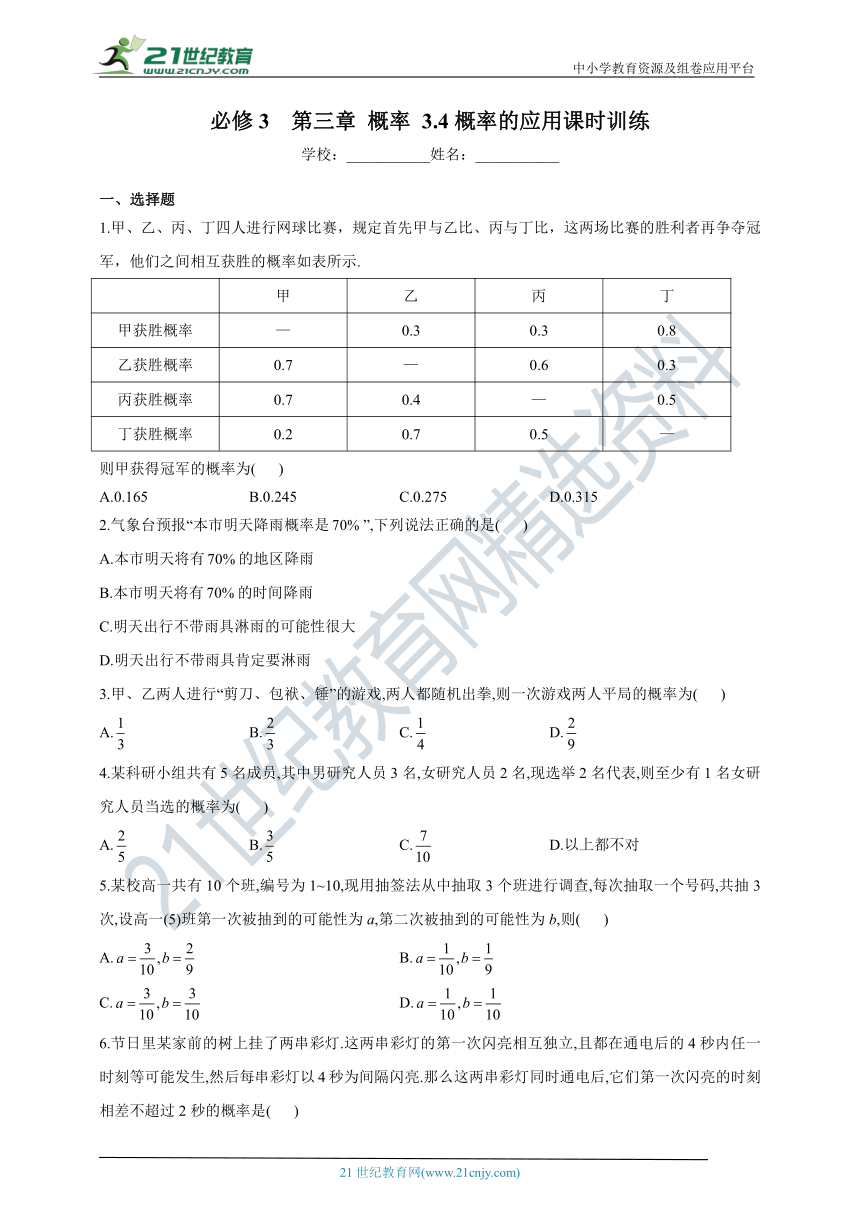
1.甲、乙、丙、丁四人进行网球比赛,规定首先甲与乙比、丙与丁比,这两场比赛的胜利者再争夺冠军,他们之间相互获胜的概率如表所示.
甲 乙 丙 丁
甲获胜概率 — 0.3 0.3 0.8
乙获胜概率 0.7 — 0.6 0.3
丙获胜概率 0.7 0.4 — 0.5
丁获胜概率 0.2 0.7 0.5 —
则甲获得冠军的概率为( )
A.0.165 B.0.245 C.0.275 D.0.315
2.气象台预报“本市明天降雨概率是”,下列说法正确的是( )
A.本市明天将有的地区降雨
B.本市明天将有的时间降雨
C.明天出行不带雨具淋雨的可能性很大
D.明天出行不带雨具肯定要淋雨
3.甲、乙两人进行“剪刀、包袱、锤”的游戏,两人都随机出拳,则一次游戏两人平局的概率为( )
A. B. C. D.
4.某科研小组共有5名成员,其中男研究人员3名,女研究人员2名,现选举2名代表,则至少有1名女研究人员当选的概率为( )
A. B. C. D.以上都不对
5.某校高一共有10个班,编号为1~10,现用抽签法从中抽取3个班进行调查,每次抽取一个号码,共抽3次,设高一(5)班第一次被抽到的可能性为a,第二次被抽到的可能性为b,则( )
A. B.
C. D.
6.节日里某家前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( )
A. B. C. D.
7.已知某人每天早晨乘坐的某一班公共汽车的准时到站的概率为,则他在天乘车中,此班车恰有天准时到站的概率为(???? )
A. B. ? C. D.
8.若,,其中,则等于( )
A. B. C. D.
二、填空题
9.连掷两次骰子得到的点数分别为和,记向量与向量的夹角为,则为直角的概率是__________.
10.去年,相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计,其频率分布如下表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为__________万元.
11.把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为__________.
12.已知函数,当时,有.给出以下结论:
①;②;③;④.
其中正确的结论序号为___________.
13.某篮球运动员在三分投球的命中率是,他投球5次,恰好投进2个的概率是_____________
三、解答题
14.一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立.
1.设每盘游戏获得的分数为X,求X的分布列;
2.玩三盘游戏,至少有一盘出现音乐的概率是多少?
3.玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
15.在某商场的有奖销售中,购满100元商品得1张奖券,多购多得.1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为,求:
(1);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
参考答案
1.答案:A
解析:假设为甲胜乙的概率,为甲胜丙的概率,为甲胜丁的概率,分别为丙胜丁和丁胜丙的概率,为甲夺冠的概率.则.
2.答案:C
解析:气象台预报“本市明天降雨概率是”,则本市明天降雨的可能性比较大,因此明天出行不带雨具淋雨的可能性很大.故选C.
3.答案:A
解析:甲、乙两人进行“剪刀、包袱、锤”的游戏,所有可能出现的情况列表如下:
锤 剪刀 包袱
锤 (锤、锤) (锤、剪刀) (锤、包袱)
剪刀 (剪刀、锤) (剪刀、剪刀) (剪刀、包袱)
包袱 (包袱、锤) (包袱、剪刀) (包袱、包袱)
由表格可知,共有9种等可能情况,其中平局的情况有3种:
(锤、锤),(剪刀、剪刀),(包袱、包袱).
因此一次游戏两人平局的概率为.故选A.
4.答案:C
解析:设3名男研究人员为两名女研究人员为,则任选举2名代表有,共10种情况,其中至少有1名女研究人员当选的情况有7种,故所求概率.故选C.
5.答案:D
解析:由简单随机抽样的定义知,每个个体在每次抽取中都有相同的可能性被抽到,故高一(5)班在第一次抽取中被抽到的可能性是,第二次被抽到的可能性为.
6.答案:C
7.答案:B
解析:某人每天早晨乘坐的某一班公共汽车的准时到站的概率为,
则他在3天乘车中,此班车恰有2天准时到站的概率为:
.
故选:B.
8.答案:C
解析:
故答案选 C.
9.答案:
解析:由向量垂直的充要条件可得,满足题意时有: ?,即: ,,满足题意的事件有6种,则为直角的概率是.
10.答案:48
解析:设游客人数最多的那一天的营业额为x万元,由题意得,解得,故游客人数最多的那一天的营业额约为48万元.
11.答案:
解析:通过做大量重复试验可以发现,正面朝上的频率都在0.5附近摆动,故掷一次硬币正面朝上的概率是0.5.
12.答案:①④
解析:根据题意,作图如下:
如图所示:.
故①④正确
故答案为:①④
13.答案:
14.答案:1.X可能的取值为:10,20,100,-200.
根据题意,有
,
,
,
所以的分布列为
X 10 20 100 -200
P
2.设“第i盘游戏没有出现音乐”为事件,则
所以“三盘游戏中至少有一次出现音乐”的概率为
因此,玩三盘游戏至少有一盘出现音乐的概率是.
3.X的数学期望为.
这表明,获得分数X的均值为负,因此,多次游戏之后分数减少的可能性更大.
15.答案:(1).
故事件的概率分别为.
(2)1张奖券中奖包含中特等奖、一等奖、二等奖三种情况.
设“1张奖券中奖”这个事件为M,则.
∵两两互斥,
∴.
故1张奖券的中奖概率为.
(3)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”互为对立事件,
∴.
故1张奖券不中特等奖且不中一等奖的概率为.
_21?????????è?????(www.21cnjy.com)_
必修3 第三章 概率 3.4概率的应用课时训练
学校:___________姓名:___________
一、选择题
1.甲、乙、丙、丁四人进行网球比赛,规定首先甲与乙比、丙与丁比,这两场比赛的胜利者再争夺冠军,他们之间相互获胜的概率如表所示.
甲 乙 丙 丁
甲获胜概率 — 0.3 0.3 0.8
乙获胜概率 0.7 — 0.6 0.3
丙获胜概率 0.7 0.4 — 0.5
丁获胜概率 0.2 0.7 0.5 —
则甲获得冠军的概率为( )
A.0.165 B.0.245 C.0.275 D.0.315
2.气象台预报“本市明天降雨概率是”,下列说法正确的是( )
A.本市明天将有的地区降雨
B.本市明天将有的时间降雨
C.明天出行不带雨具淋雨的可能性很大
D.明天出行不带雨具肯定要淋雨
3.甲、乙两人进行“剪刀、包袱、锤”的游戏,两人都随机出拳,则一次游戏两人平局的概率为( )
A. B. C. D.
4.某科研小组共有5名成员,其中男研究人员3名,女研究人员2名,现选举2名代表,则至少有1名女研究人员当选的概率为( )
A. B. C. D.以上都不对
5.某校高一共有10个班,编号为1~10,现用抽签法从中抽取3个班进行调查,每次抽取一个号码,共抽3次,设高一(5)班第一次被抽到的可能性为a,第二次被抽到的可能性为b,则( )
A. B.
C. D.
6.节日里某家前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( )
A. B. C. D.
7.已知某人每天早晨乘坐的某一班公共汽车的准时到站的概率为,则他在天乘车中,此班车恰有天准时到站的概率为(???? )
A. B. ? C. D.
8.若,,其中,则等于( )
A. B. C. D.
二、填空题
9.连掷两次骰子得到的点数分别为和,记向量与向量的夹角为,则为直角的概率是__________.
10.去年,相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计,其频率分布如下表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为__________万元.
11.把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为__________.
12.已知函数,当时,有.给出以下结论:
①;②;③;④.
其中正确的结论序号为___________.
13.某篮球运动员在三分投球的命中率是,他投球5次,恰好投进2个的概率是_____________
三、解答题
14.一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立.
1.设每盘游戏获得的分数为X,求X的分布列;
2.玩三盘游戏,至少有一盘出现音乐的概率是多少?
3.玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
15.在某商场的有奖销售中,购满100元商品得1张奖券,多购多得.1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为,求:
(1);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
参考答案
1.答案:A
解析:假设为甲胜乙的概率,为甲胜丙的概率,为甲胜丁的概率,分别为丙胜丁和丁胜丙的概率,为甲夺冠的概率.则.
2.答案:C
解析:气象台预报“本市明天降雨概率是”,则本市明天降雨的可能性比较大,因此明天出行不带雨具淋雨的可能性很大.故选C.
3.答案:A
解析:甲、乙两人进行“剪刀、包袱、锤”的游戏,所有可能出现的情况列表如下:
锤 剪刀 包袱
锤 (锤、锤) (锤、剪刀) (锤、包袱)
剪刀 (剪刀、锤) (剪刀、剪刀) (剪刀、包袱)
包袱 (包袱、锤) (包袱、剪刀) (包袱、包袱)
由表格可知,共有9种等可能情况,其中平局的情况有3种:
(锤、锤),(剪刀、剪刀),(包袱、包袱).
因此一次游戏两人平局的概率为.故选A.
4.答案:C
解析:设3名男研究人员为两名女研究人员为,则任选举2名代表有,共10种情况,其中至少有1名女研究人员当选的情况有7种,故所求概率.故选C.
5.答案:D
解析:由简单随机抽样的定义知,每个个体在每次抽取中都有相同的可能性被抽到,故高一(5)班在第一次抽取中被抽到的可能性是,第二次被抽到的可能性为.
6.答案:C
7.答案:B
解析:某人每天早晨乘坐的某一班公共汽车的准时到站的概率为,
则他在3天乘车中,此班车恰有2天准时到站的概率为:
.
故选:B.
8.答案:C
解析:
故答案选 C.
9.答案:
解析:由向量垂直的充要条件可得,满足题意时有: ?,即: ,,满足题意的事件有6种,则为直角的概率是.
10.答案:48
解析:设游客人数最多的那一天的营业额为x万元,由题意得,解得,故游客人数最多的那一天的营业额约为48万元.
11.答案:
解析:通过做大量重复试验可以发现,正面朝上的频率都在0.5附近摆动,故掷一次硬币正面朝上的概率是0.5.
12.答案:①④
解析:根据题意,作图如下:
如图所示:.
故①④正确
故答案为:①④
13.答案:
14.答案:1.X可能的取值为:10,20,100,-200.
根据题意,有
,
,
,
所以的分布列为
X 10 20 100 -200
P
2.设“第i盘游戏没有出现音乐”为事件,则
所以“三盘游戏中至少有一次出现音乐”的概率为
因此,玩三盘游戏至少有一盘出现音乐的概率是.
3.X的数学期望为.
这表明,获得分数X的均值为负,因此,多次游戏之后分数减少的可能性更大.
15.答案:(1).
故事件的概率分别为.
(2)1张奖券中奖包含中特等奖、一等奖、二等奖三种情况.
设“1张奖券中奖”这个事件为M,则.
∵两两互斥,
∴.
故1张奖券的中奖概率为.
(3)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”互为对立事件,
∴.
故1张奖券不中特等奖且不中一等奖的概率为.
_21?????????è?????(www.21cnjy.com)_
