六年级下册数学课件-6 整理与复习 1 数与代数 第6课时 比和比例 人教版(共13张PPT)
文档属性
| 名称 | 六年级下册数学课件-6 整理与复习 1 数与代数 第6课时 比和比例 人教版(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 00:00:00 | ||
图片预览




文档简介
整理和复习
1 数与代数
6
第6课时 比和比例
情境导入
15cm
10cm
这面联合国国旗长和宽的最简单的整数比是多少?
在上册教材中我们学
习了比的知识,回顾课本
上的例题,大家还记得比
的相关知识吗?
关于比和比例的知识,你知道什么?
它们有什么区别和联系?
比
比例
意义
各部分名称
基本性质
新课探究
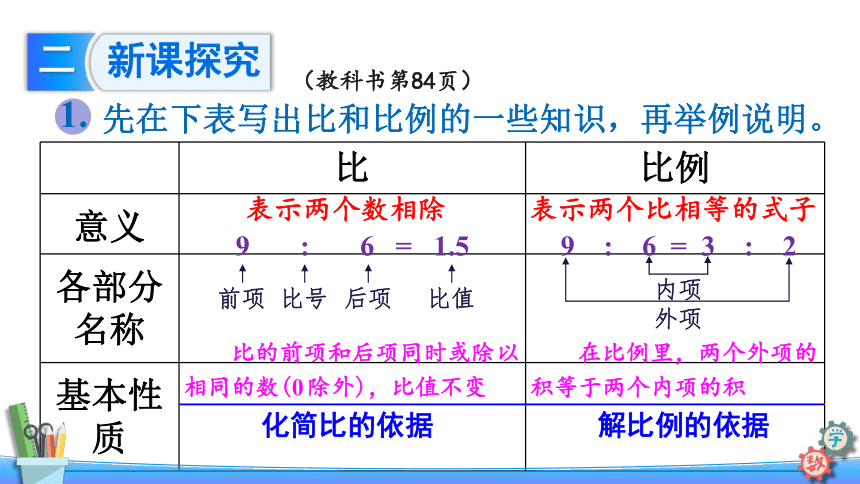
先在下表写出比和比例的一些知识,再举例说明。
1.
(教科书第84页)
表示两个数相除
表示两个比相等的式子
9 : 6 = 1.5
前项
比号
后项
比值
9 : 6 = 3 : 2
内项
外项
比的前项和后项同时或除以
相同的数(0除外),比值不变
在比例里,两个外项的
积等于两个内项的积
化简比的依据
解比例的依据
比和分数、除法有什么联系?先填写下表,再说
一说它们的区别。
2.
被除数
除号
除数
商
前项
比号
后项
比值
5:8
5÷8=0.625
分数是一种数。
除法是数与数之间的运算。
比是一种关系。
比的基本性质、分数的基本性质、商不变的规律之
间有什么联系?
3.
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的分子和分母同时乘或除以相同的数(0除外),分数值不变。
被除数和除数同时乘或除以相同的数(0除外),商不变。
比的前项相当于除法里的被除数,分数里的分子。
比的后项相当于除法里的除数,分数里的分母。
比值相当于除法里的商,相当于分数里的分数值。
两种相关联的量,一种量变化,另一种量也随
着变化,如果这两种量中相对应的两个数的比值一
定,这种量就叫做
如果这两种量中相对应的两个数的乘积一定,
这种量就叫做
你怎么判断两种相关联的量是成正比例关系还是成
反比例关系?请举生活中的实例加以说明。
4.
正比例关系。
反比例关系。
工作效率一定,工作时间与工作总量成正比例。
速度一定,时间与路程成正比例。
路程一定,时间和速度成反比例。
总价一定,单价和数量成反比例。
随堂练习
1.
判断下列各题中的两种量是不是成比例。如果成比
例,成什么比例?
?
修一条路,每天修路的米数和所需要的天数。( )
?
三角形的高一定,对应的底边长和面积。 ( )
?
圆的半径一定,圆的周长和圆周率。 ( )
?
圆的半径和面积。 ( )
反比例
正比例
×
×
2.
在比例尺是1:3000000的地图上,甲、乙两地相距
4.5cm。一辆车从甲地开往乙地,每小时行45km,
几小时可以到达?
4.5×3000000=13500000(cm)=135km
135÷45=3(小时)
答:3小时可以到达。
培优训练
用边长为0.3dm的方砖铺一条小路,需要2400块,
如果改用边长为0.4dm的方砖,需要多少块?
1.
解:设需要x块。
0.4×0.4x= 0.3×0.3×2400
0.16x=216
x=1350
答:需要1350块。
0.3dm
0.4dm
2.
一个长方形麦地,周长240m,长与宽的比是3:2,
这块麦地的面积是多少平方米?合多少公顷?
240÷2÷(2+3)=24(m)
(24×3)×(24×2)=3456(m2)=0.3456公顷
答:这块麦地的面积是3456平方米,
合0.3456公顷。
3.
甲、乙、丙三个村合修一条路,三个村所修长度的比
为8:7:5,现在三个村要按所修长度之比派谴劳动力。丙村由于
特殊原因,没有派遣劳动力,但需付给甲、乙两村15000元,
甲村派出50人,乙村派出30人。甲、乙两村各应分得多少钱?
每份的人数:(50+30)÷(8+7+5)=4(人)
甲村多派的人数:50?8×4=18(人)
乙村多派的人数:30?7×4=2(人)
答:甲村应分得135000元,乙村应分得1500元。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1 数与代数
6
第6课时 比和比例
情境导入
15cm
10cm
这面联合国国旗长和宽的最简单的整数比是多少?
在上册教材中我们学
习了比的知识,回顾课本
上的例题,大家还记得比
的相关知识吗?
关于比和比例的知识,你知道什么?
它们有什么区别和联系?
比
比例
意义
各部分名称
基本性质
新课探究
先在下表写出比和比例的一些知识,再举例说明。
1.
(教科书第84页)
表示两个数相除
表示两个比相等的式子
9 : 6 = 1.5
前项
比号
后项
比值
9 : 6 = 3 : 2
内项
外项
比的前项和后项同时或除以
相同的数(0除外),比值不变
在比例里,两个外项的
积等于两个内项的积
化简比的依据
解比例的依据
比和分数、除法有什么联系?先填写下表,再说
一说它们的区别。
2.
被除数
除号
除数
商
前项
比号
后项
比值
5:8
5÷8=0.625
分数是一种数。
除法是数与数之间的运算。
比是一种关系。
比的基本性质、分数的基本性质、商不变的规律之
间有什么联系?
3.
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的分子和分母同时乘或除以相同的数(0除外),分数值不变。
被除数和除数同时乘或除以相同的数(0除外),商不变。
比的前项相当于除法里的被除数,分数里的分子。
比的后项相当于除法里的除数,分数里的分母。
比值相当于除法里的商,相当于分数里的分数值。
两种相关联的量,一种量变化,另一种量也随
着变化,如果这两种量中相对应的两个数的比值一
定,这种量就叫做
如果这两种量中相对应的两个数的乘积一定,
这种量就叫做
你怎么判断两种相关联的量是成正比例关系还是成
反比例关系?请举生活中的实例加以说明。
4.
正比例关系。
反比例关系。
工作效率一定,工作时间与工作总量成正比例。
速度一定,时间与路程成正比例。
路程一定,时间和速度成反比例。
总价一定,单价和数量成反比例。
随堂练习
1.
判断下列各题中的两种量是不是成比例。如果成比
例,成什么比例?
?
修一条路,每天修路的米数和所需要的天数。( )
?
三角形的高一定,对应的底边长和面积。 ( )
?
圆的半径一定,圆的周长和圆周率。 ( )
?
圆的半径和面积。 ( )
反比例
正比例
×
×
2.
在比例尺是1:3000000的地图上,甲、乙两地相距
4.5cm。一辆车从甲地开往乙地,每小时行45km,
几小时可以到达?
4.5×3000000=13500000(cm)=135km
135÷45=3(小时)
答:3小时可以到达。
培优训练
用边长为0.3dm的方砖铺一条小路,需要2400块,
如果改用边长为0.4dm的方砖,需要多少块?
1.
解:设需要x块。
0.4×0.4x= 0.3×0.3×2400
0.16x=216
x=1350
答:需要1350块。
0.3dm
0.4dm
2.
一个长方形麦地,周长240m,长与宽的比是3:2,
这块麦地的面积是多少平方米?合多少公顷?
240÷2÷(2+3)=24(m)
(24×3)×(24×2)=3456(m2)=0.3456公顷
答:这块麦地的面积是3456平方米,
合0.3456公顷。
3.
甲、乙、丙三个村合修一条路,三个村所修长度的比
为8:7:5,现在三个村要按所修长度之比派谴劳动力。丙村由于
特殊原因,没有派遣劳动力,但需付给甲、乙两村15000元,
甲村派出50人,乙村派出30人。甲、乙两村各应分得多少钱?
每份的人数:(50+30)÷(8+7+5)=4(人)
甲村多派的人数:50?8×4=18(人)
乙村多派的人数:30?7×4=2(人)
答:甲村应分得135000元,乙村应分得1500元。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
