26.1.2 反比例函数的图象和性质应用(第2课时) 课件(共25张PPT)
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质应用(第2课时) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览







文档简介
26.1.2 反比例函数的图象和性质
第2课时 反比例函数的图象和性质的综合运用
第二十六章 反比例函数
人教版数学九年级下册
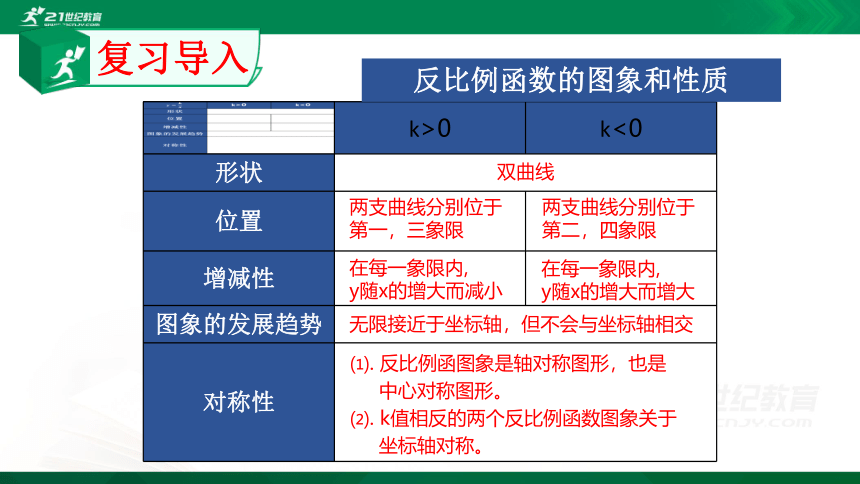
k>0
k<0
形状
位置
增减性
图象的发展趋势
对称性
反比例函数的图象和性质
双曲线
两支曲线分别位于第一,三象限
两支曲线分别位于第二,四象限
在每一象限内,
y随x的增大而减小
在每一象限内,
y随x的增大而增大
无限接近于坐标轴,但不会与坐标轴相交
⑴. 反比例函图象是轴对称图形,也是
中心对称图形。
⑵. k值相反的两个反比例函数图象关于
坐标轴对称。
复习导入
1
理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算中. (重点、难点)
2
能够解决反比例函数与一次函数的综合性问题.
(重点、难点)
3
体会“数”与“形”的相互转化,学习数形结合的思想方法,进一步提高对反比例函数相关知识的综合运
用能力. (重点、难点)
学习目标
一、反比例函数解析式中 k 的几何意义
1. 在反比例函数 的图象上分别取点A,B,C向
x 轴、y 轴作垂线,围成面积分别为S1 ,S2 ,S3的
矩形, 通过计算说明S1 ,S2 ,S3有什么数量关系?
合作探究
S1=S2=S3=4
猜想:反比例函数图象上任意一点向坐标轴作垂线,
这一点与坐标轴围成的矩形面积与k的关系
矩形面积与k值相等
探究新知
一、反比例函数解析式中 k 的几何意义
合作探究
1. 在反比例函数 的图象上分别取点A,B,C向
x 轴、y 轴作垂线,围成面积分别为S1 ,S2 ,S3的
矩形,则S1 ,S2 ,S3有什么数量关系?
S1=S2=S3=4
猜想:反比例函数图象上任意一点向坐标轴作垂线,
这一点与坐标轴围成的矩形面积与k的关系
矩形面积与|K|相等
一、反比例函数解析式中 k 的几何意义
若点P是 图象上的任意一点,作 PM⊥x 轴于M,
作 PN⊥y 轴于N,矩形 PMON的面积与k的关系是:
S矩形 PMON = PM · PN
= |m| · |n|
= |mn|
= |K|
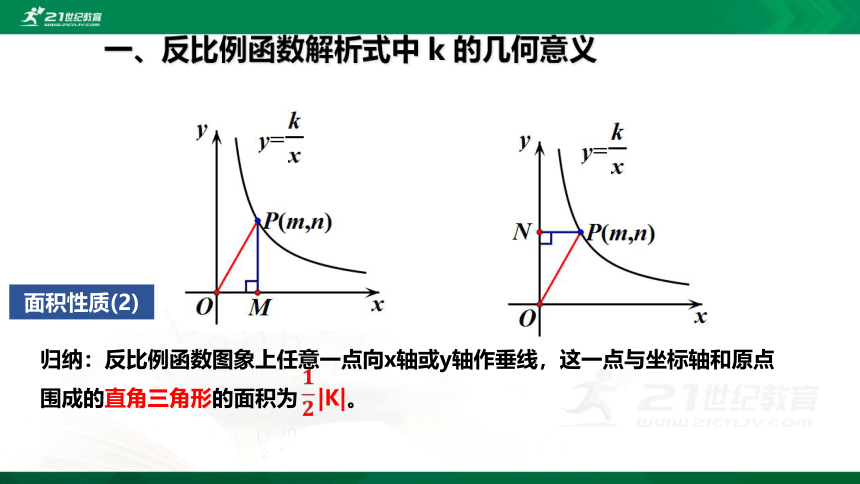
面积性质(1)
归纳:反比例函数图象上任意一点向坐标轴作垂线,这一点与坐标轴围成的矩形面积为|K|。
反比例函数图象的面积不变性。
一、反比例函数解析式中 k 的几何意义
若点P是 图象上的任意一点,作 PM⊥x 轴于M,
作 PN⊥y 轴于N,连接OP,则Rt△POM和Rt △PON
的面积和k的关系是:
S△POM= S△PON= |K|
?
思 考
一、反比例函数解析式中 k 的几何意义
面积性质(2)
归纳:反比例函数图象上任意一点向x轴或y轴作垂线,这一点与坐标轴和原点围成的直角三角形的面积为 |K|。
?
例1:如图所示,点A在反比例函数 的图象上,
AC垂直 x 轴于点 C,且 △AOC 的面积为 3,求该反
比例函数的表达式.
解:∵点 A 在反比例函数的图象上,且AC⊥X轴,
∴ S△AOC= |K|=3,
∴ |K|=6,
又∵反比例函数的图象位于第一,三象限
∴ K>0,
∴ K=6, ∴反比例函数的表达式为
?
例题讲解
1. 如图,过反比例函数 图象上的一点 P,
作 PA⊥x 轴于A. 若△POA 的面积为 6,
则 k = .
-12
y
x
O
P
A
2. 若点 P 是反比例函数图象上的一点,过点 P 分别向x 轴、y 轴作垂线,垂足分别为点 M,N,若四边形PMON 的面积为 3,则这个反比例函数的关系式是 。
或
针对练习
3. 如图,P,C是函数 (x>0) 图象上的任意两点,PA,CD 分别垂直 x 轴于A,D。
(1)若△POA的面积为 S1,则S1= ;
(2)若梯形CEAD的面积为 S2,△POE的面积为S3,则S3 和 S2 的大小关系是S2 S3.
2
=
4. 如图所示,直线与双曲线交于 A,B 两点,
P是线段AB上的点,若设△AOC的面积为S1,
△BOD的面积为S2,△POE的面积为S3 ,则
S1,S2,S3的大小关系为 .
S1 = S2 < S3
F
例2:如图,点A是反比例函数 (x>0)的图象上任意一点,AB//x轴交反比例函数 (x<0) 的图象于点 B,以 AB 为边作平行四边形 ABCD,其中点 C,D 在 x 轴上,则 S平行四边形ABCD = .
y
D
B
A
C
x
3
2
5
方法总结:解决反比例函数有关的面积问题,可以把原图形通过切割、平移等变换,转化为较容易求面积的图形.
O
例题讲解
二、反比例函数与一次函数的综合
例3: 已知 A(a, ),B(-1,2)是一次函数 y= kx+b与反比例函数
图象的两个交点,求m的值及一次函数解析式 .
解:把 B (-1,2)代入 中,
得 m =-1×2=-2.
把A(-4, ),B(-1,2)代入y=kx+b中,得
-4k + b = ,
-k + b =2,
k =
解得
b =
所以一次函数的解析式为 y = x + .
?
?
所以A点坐标为 (-4, )
例题讲解
二、反比例函数与一次函数的综合
例4: 如图是一次函数 y1=kx+b 和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 .
-2
3
y
x
0
-23
解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,
可知-2< x <0 或 x >3.
方法总结:对于一些题目,借助函数图象比较
大小更加简洁明了.
例题讲解
2. 如图,一次函数 y1= k1x+b (k1≠0) 的图象
与反比例函数 的图象交于 A,B 两点,
观察图象,当y1>y2时,
x 的取值范围是 .
-1
2
y
x
0
A
B
-12
1. 反比例函数 的图象与正比例函数 y = 3x 的图象的交点坐标为 .
(2,6),(-2,-6)
针对练习
3. 如图,直线y=ax+b与反比例函数 (x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定一次函数及反比例函数的解析式;
(2)求△AOC的面积
(3)试确定 的取值范围
?
面积问题
与一次函数的综合
反比例函数图像和性质的综合运用
常见题型:
联立求交点 ,求解析式
求图形面积
利用图象求自变量取值范围
面积不变性
课堂小结
A. 4 B. 2
C. -2 D.不确定
1. 如图所示, P 是反比例函数 的图象上一点,
过点 P 作 PB ⊥x 轴于点 B,点 A 在 y 轴上,
△ABP 的面积为 2,则 k 的值为( )
O
B
A
P
x
y
A
课堂练习
2. 在同一直角坐标系中,函数 与 y = ax+1 (a≠0) 的图象可能是 ( )
A.
y
x
O
B.
y
x
O
C.
y
x
O
D.
y
x
O
B
3. 如图,直线 y=k1x + b 与反比例函数 (x>0)
交于A,B两点,其横坐标分别为1和5,
则不等式k1x +b > 的解集是 .
1<x<5
O
B
A
x
y
1
5
4. 如图,反比例函数 与一次函数y=-x+2
的图象交于A,B两点,连接OA,OB,
则△AOB的面积为 。
O
A
y
B
x
6
x
y
O
B
A
5. 如图,直线 y=ax + b 与双曲线 交于两点
A(1,2),B(m,-4)两点,
(1) 求直线与双曲线的解析式;
(2) 求不等式 ax+b> 的解集.
x>1 或 <x<0.
y = 4x-2
如图,函数 y=-x与函数 的图象
相交于 A,B 两点,过点 A,B分别作 y 轴
的垂线,垂足分别为C,D,
则四边形ACBD的面积为 ( )
A. 2 B. 4
C. 6 D. 8
D
y
x
O
C
A
B
D
第2课时 反比例函数的图象和性质的综合运用
第二十六章 反比例函数
人教版数学九年级下册
k>0
k<0
形状
位置
增减性
图象的发展趋势
对称性
反比例函数的图象和性质
双曲线
两支曲线分别位于第一,三象限
两支曲线分别位于第二,四象限
在每一象限内,
y随x的增大而减小
在每一象限内,
y随x的增大而增大
无限接近于坐标轴,但不会与坐标轴相交
⑴. 反比例函图象是轴对称图形,也是
中心对称图形。
⑵. k值相反的两个反比例函数图象关于
坐标轴对称。
复习导入
1
理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算中. (重点、难点)
2
能够解决反比例函数与一次函数的综合性问题.
(重点、难点)
3
体会“数”与“形”的相互转化,学习数形结合的思想方法,进一步提高对反比例函数相关知识的综合运
用能力. (重点、难点)
学习目标
一、反比例函数解析式中 k 的几何意义
1. 在反比例函数 的图象上分别取点A,B,C向
x 轴、y 轴作垂线,围成面积分别为S1 ,S2 ,S3的
矩形, 通过计算说明S1 ,S2 ,S3有什么数量关系?
合作探究
S1=S2=S3=4
猜想:反比例函数图象上任意一点向坐标轴作垂线,
这一点与坐标轴围成的矩形面积与k的关系
矩形面积与k值相等
探究新知
一、反比例函数解析式中 k 的几何意义
合作探究
1. 在反比例函数 的图象上分别取点A,B,C向
x 轴、y 轴作垂线,围成面积分别为S1 ,S2 ,S3的
矩形,则S1 ,S2 ,S3有什么数量关系?
S1=S2=S3=4
猜想:反比例函数图象上任意一点向坐标轴作垂线,
这一点与坐标轴围成的矩形面积与k的关系
矩形面积与|K|相等
一、反比例函数解析式中 k 的几何意义
若点P是 图象上的任意一点,作 PM⊥x 轴于M,
作 PN⊥y 轴于N,矩形 PMON的面积与k的关系是:
S矩形 PMON = PM · PN
= |m| · |n|
= |mn|
= |K|
面积性质(1)
归纳:反比例函数图象上任意一点向坐标轴作垂线,这一点与坐标轴围成的矩形面积为|K|。
反比例函数图象的面积不变性。
一、反比例函数解析式中 k 的几何意义
若点P是 图象上的任意一点,作 PM⊥x 轴于M,
作 PN⊥y 轴于N,连接OP,则Rt△POM和Rt △PON
的面积和k的关系是:
S△POM= S△PON= |K|
?
思 考
一、反比例函数解析式中 k 的几何意义
面积性质(2)
归纳:反比例函数图象上任意一点向x轴或y轴作垂线,这一点与坐标轴和原点围成的直角三角形的面积为 |K|。
?
例1:如图所示,点A在反比例函数 的图象上,
AC垂直 x 轴于点 C,且 △AOC 的面积为 3,求该反
比例函数的表达式.
解:∵点 A 在反比例函数的图象上,且AC⊥X轴,
∴ S△AOC= |K|=3,
∴ |K|=6,
又∵反比例函数的图象位于第一,三象限
∴ K>0,
∴ K=6, ∴反比例函数的表达式为
?
例题讲解
1. 如图,过反比例函数 图象上的一点 P,
作 PA⊥x 轴于A. 若△POA 的面积为 6,
则 k = .
-12
y
x
O
P
A
2. 若点 P 是反比例函数图象上的一点,过点 P 分别向x 轴、y 轴作垂线,垂足分别为点 M,N,若四边形PMON 的面积为 3,则这个反比例函数的关系式是 。
或
针对练习
3. 如图,P,C是函数 (x>0) 图象上的任意两点,PA,CD 分别垂直 x 轴于A,D。
(1)若△POA的面积为 S1,则S1= ;
(2)若梯形CEAD的面积为 S2,△POE的面积为S3,则S3 和 S2 的大小关系是S2 S3.
2
=
4. 如图所示,直线与双曲线交于 A,B 两点,
P是线段AB上的点,若设△AOC的面积为S1,
△BOD的面积为S2,△POE的面积为S3 ,则
S1,S2,S3的大小关系为 .
S1 = S2 < S3
F
例2:如图,点A是反比例函数 (x>0)的图象上任意一点,AB//x轴交反比例函数 (x<0) 的图象于点 B,以 AB 为边作平行四边形 ABCD,其中点 C,D 在 x 轴上,则 S平行四边形ABCD = .
y
D
B
A
C
x
3
2
5
方法总结:解决反比例函数有关的面积问题,可以把原图形通过切割、平移等变换,转化为较容易求面积的图形.
O
例题讲解
二、反比例函数与一次函数的综合
例3: 已知 A(a, ),B(-1,2)是一次函数 y= kx+b与反比例函数
图象的两个交点,求m的值及一次函数解析式 .
解:把 B (-1,2)代入 中,
得 m =-1×2=-2.
把A(-4, ),B(-1,2)代入y=kx+b中,得
-4k + b = ,
-k + b =2,
k =
解得
b =
所以一次函数的解析式为 y = x + .
?
?
所以A点坐标为 (-4, )
例题讲解
二、反比例函数与一次函数的综合
例4: 如图是一次函数 y1=kx+b 和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 .
-2
3
y
x
0
-2
解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,
可知-2< x <0 或 x >3.
方法总结:对于一些题目,借助函数图象比较
大小更加简洁明了.
例题讲解
2. 如图,一次函数 y1= k1x+b (k1≠0) 的图象
与反比例函数 的图象交于 A,B 两点,
观察图象,当y1>y2时,
x 的取值范围是 .
-1
2
y
x
0
A
B
-1
1. 反比例函数 的图象与正比例函数 y = 3x 的图象的交点坐标为 .
(2,6),(-2,-6)
针对练习
3. 如图,直线y=ax+b与反比例函数 (x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定一次函数及反比例函数的解析式;
(2)求△AOC的面积
(3)试确定 的取值范围
?
面积问题
与一次函数的综合
反比例函数图像和性质的综合运用
常见题型:
联立求交点 ,求解析式
求图形面积
利用图象求自变量取值范围
面积不变性
课堂小结
A. 4 B. 2
C. -2 D.不确定
1. 如图所示, P 是反比例函数 的图象上一点,
过点 P 作 PB ⊥x 轴于点 B,点 A 在 y 轴上,
△ABP 的面积为 2,则 k 的值为( )
O
B
A
P
x
y
A
课堂练习
2. 在同一直角坐标系中,函数 与 y = ax+1 (a≠0) 的图象可能是 ( )
A.
y
x
O
B.
y
x
O
C.
y
x
O
D.
y
x
O
B
3. 如图,直线 y=k1x + b 与反比例函数 (x>0)
交于A,B两点,其横坐标分别为1和5,
则不等式k1x +b > 的解集是 .
1<x<5
O
B
A
x
y
1
5
4. 如图,反比例函数 与一次函数y=-x+2
的图象交于A,B两点,连接OA,OB,
则△AOB的面积为 。
O
A
y
B
x
6
x
y
O
B
A
5. 如图,直线 y=ax + b 与双曲线 交于两点
A(1,2),B(m,-4)两点,
(1) 求直线与双曲线的解析式;
(2) 求不等式 ax+b> 的解集.
x>1 或 <x<0.
y = 4x-2
如图,函数 y=-x与函数 的图象
相交于 A,B 两点,过点 A,B分别作 y 轴
的垂线,垂足分别为C,D,
则四边形ACBD的面积为 ( )
A. 2 B. 4
C. 6 D. 8
D
y
x
O
C
A
B
D
