28.1 余弦正切(第2课时) 课件(共19张PPT)
文档属性
| 名称 | 28.1 余弦正切(第2课时) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 21:14:17 | ||
图片预览





文档简介
28.1 锐角三角函数
第2课时 余弦和正切
第二十八章 锐角三角函数
人教版数学九年级下册
1
认识并理解余弦、正切的概念进而得到锐角三角函数的概念. (重点)
2
能灵活运用锐角三角函数进行相关运算. (重点、难点)
学习目标
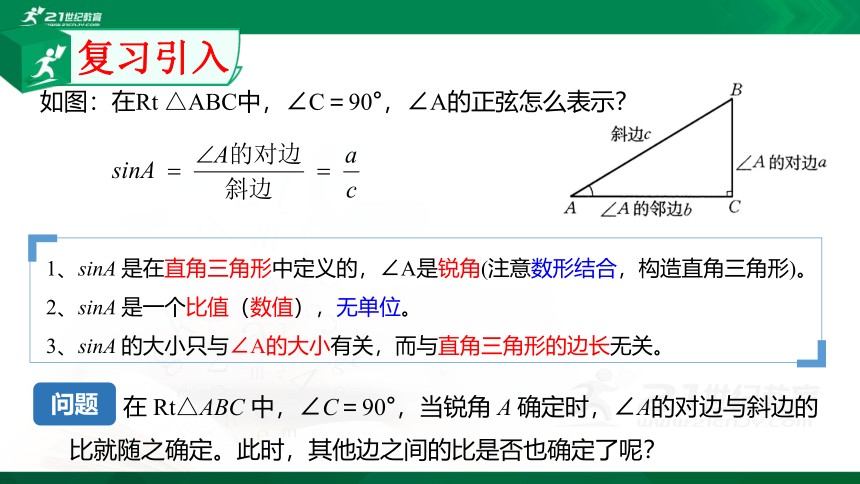
如图:在Rt △ABC中,∠C=90°,∠A的正弦怎么表示?
问题
在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也确定了呢?
1、sinA 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA 是一个比值(数值),无单位。
3、sinA 的大小只与∠A的大小有关,而与直角三角形的边长无关。
复习引入
一、余弦的概念
自主探究
如图所示, △ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
方法一:
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
方法二:
∵∠A=∠D,∠C=∠F=90°,
∴∠B=∠E,
∴ sinB = sinE,
∴
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的邻边与斜边的比值也是一个固定值。
探究新知
一、余弦的概念
知识归纳
在直角三角形中,我们把锐角A的邻边与斜边的比叫做
∠A的余弦,
记作 cos A 。
?
?
知识点拨
若:∠A + ∠B=90°
则: sinA = cosB
cosA = sinB
1. 如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,
cosA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,
垂足为D。
A
B
C
D
AD
AB
BD
AB
?
?
针对练习
A
B
C
8
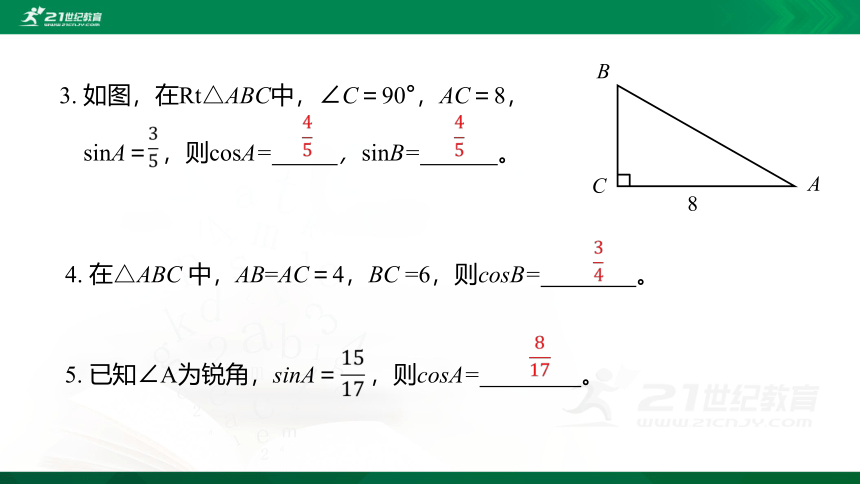
3. 如图,在Rt△ABC中,∠C=90°,AC=8,
sinA= ,则cosA= ,sinB= 。
?
4. 在△ABC 中,AB=AC=4,BC =6,则cosB= 。
5. 已知∠A为锐角,sinA= ,则cosA= 。
?
?
?
?
?
二、正切的概念
自主探究
如图所示, △ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的对边与邻边的比值也是一个固定值。
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
?
∴
?
探究新知
二、正切的概念
知识归纳
在直角三角形中,我们把锐角A的对边与邻边的比叫做
∠A的正切,
记作 tan A 。
?
?
若:∠A + ∠B=90° 则:tan A· tan B=1
思 考
如果两个角互余,那么这两个角的正切值有什么关系?
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),则 OP 与 x 轴正方向所夹锐角 α 的正切值为 .
2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.
?
A
C
A
B
针对练习
三、锐角三角函数
∟
B
A
C
斜边
对边
邻边
对于锐角 A 的每一个值,sinA 有唯一的值和它对应,所以 sinA 是锐角 A 的函数。
同样地,cosA,tanA 也是锐角 A 的函数。
锐角 A 的正弦、余弦、正切都叫做∠A的三角函数。
探究新知
三、锐角三角函数
例:如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,
求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
例题讲解
1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
A
B
C
8
2. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8,tanA= ,
则sinA= ,cosB = .
?
?
针对练习
余弦和正切
余弦函数的概念
性 质
若:∠A + ∠B=90°
则: sinA = cosB
cosA = sinB
tan A· tan B=1
?
正切函数的概念
?
课堂小结
2. 随着锐角 α 的增大,cosα 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,
∠A=35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
B
当 0°<α<90°时,cos α 的值随着角度的增大而减小。
课堂练习
3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为: .
=
=
∠A +∠B = 90°
4. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,
垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.
解: ∵ ∠ACB= ∠ADC =90°,
∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,
∴∠B = ∠ACD,
∴ tan∠B = tan∠ACD =
5. sin70°,cos70°,tan70°的大小关系是 ( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
解析:根据锐角三角函数的概念,
知 sin70°<1,cos70°<1,tan70°>1.
又∵cos70°=sin20°,正弦值随着角的增大而增大,
∴sin70°>cos70°=sin20°.
故选D.
D
第2课时 余弦和正切
第二十八章 锐角三角函数
人教版数学九年级下册
1
认识并理解余弦、正切的概念进而得到锐角三角函数的概念. (重点)
2
能灵活运用锐角三角函数进行相关运算. (重点、难点)
学习目标
如图:在Rt △ABC中,∠C=90°,∠A的正弦怎么表示?
问题
在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也确定了呢?
1、sinA 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA 是一个比值(数值),无单位。
3、sinA 的大小只与∠A的大小有关,而与直角三角形的边长无关。
复习引入
一、余弦的概念
自主探究
如图所示, △ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
方法一:
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
方法二:
∵∠A=∠D,∠C=∠F=90°,
∴∠B=∠E,
∴ sinB = sinE,
∴
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的邻边与斜边的比值也是一个固定值。
探究新知
一、余弦的概念
知识归纳
在直角三角形中,我们把锐角A的邻边与斜边的比叫做
∠A的余弦,
记作 cos A 。
?
?
知识点拨
若:∠A + ∠B=90°
则: sinA = cosB
cosA = sinB
1. 如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,
cosA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,
垂足为D。
A
B
C
D
AD
AB
BD
AB
?
?
针对练习
A
B
C
8
3. 如图,在Rt△ABC中,∠C=90°,AC=8,
sinA= ,则cosA= ,sinB= 。
?
4. 在△ABC 中,AB=AC=4,BC =6,则cosB= 。
5. 已知∠A为锐角,sinA= ,则cosA= 。
?
?
?
?
?
二、正切的概念
自主探究
如图所示, △ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的对边与邻边的比值也是一个固定值。
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
?
∴
?
探究新知
二、正切的概念
知识归纳
在直角三角形中,我们把锐角A的对边与邻边的比叫做
∠A的正切,
记作 tan A 。
?
?
若:∠A + ∠B=90° 则:tan A· tan B=1
思 考
如果两个角互余,那么这两个角的正切值有什么关系?
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),则 OP 与 x 轴正方向所夹锐角 α 的正切值为 .
2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.
?
A
C
A
B
针对练习
三、锐角三角函数
∟
B
A
C
斜边
对边
邻边
对于锐角 A 的每一个值,sinA 有唯一的值和它对应,所以 sinA 是锐角 A 的函数。
同样地,cosA,tanA 也是锐角 A 的函数。
锐角 A 的正弦、余弦、正切都叫做∠A的三角函数。
探究新知
三、锐角三角函数
例:如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,
求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
例题讲解
1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
A
B
C
8
2. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8,tanA= ,
则sinA= ,cosB = .
?
?
针对练习
余弦和正切
余弦函数的概念
性 质
若:∠A + ∠B=90°
则: sinA = cosB
cosA = sinB
tan A· tan B=1
?
正切函数的概念
?
课堂小结
2. 随着锐角 α 的增大,cosα 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,
∠A=35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
B
当 0°<α<90°时,cos α 的值随着角度的增大而减小。
课堂练习
3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为: .
=
=
∠A +∠B = 90°
4. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,
垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.
解: ∵ ∠ACB= ∠ADC =90°,
∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,
∴∠B = ∠ACD,
∴ tan∠B = tan∠ACD =
5. sin70°,cos70°,tan70°的大小关系是 ( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
解析:根据锐角三角函数的概念,
知 sin70°<1,cos70°<1,tan70°>1.
又∵cos70°=sin20°,正弦值随着角的增大而增大,
∴sin70°>cos70°=sin20°.
故选D.
D
