人教版七年级下册数学 5.3.1平行线的性质 同步测试(Word版 含解析)
文档属性
| 名称 | 人教版七年级下册数学 5.3.1平行线的性质 同步测试(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 20:40:49 | ||
图片预览


文档简介
5.3.1平行线的性质
同步测试
一.选择题
1.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
2.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75°
B.60°
C.45°
D.30°
3.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80°
B.90°
C.100°
D.110°
4.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40°
B.45°
C.50°
D.60°
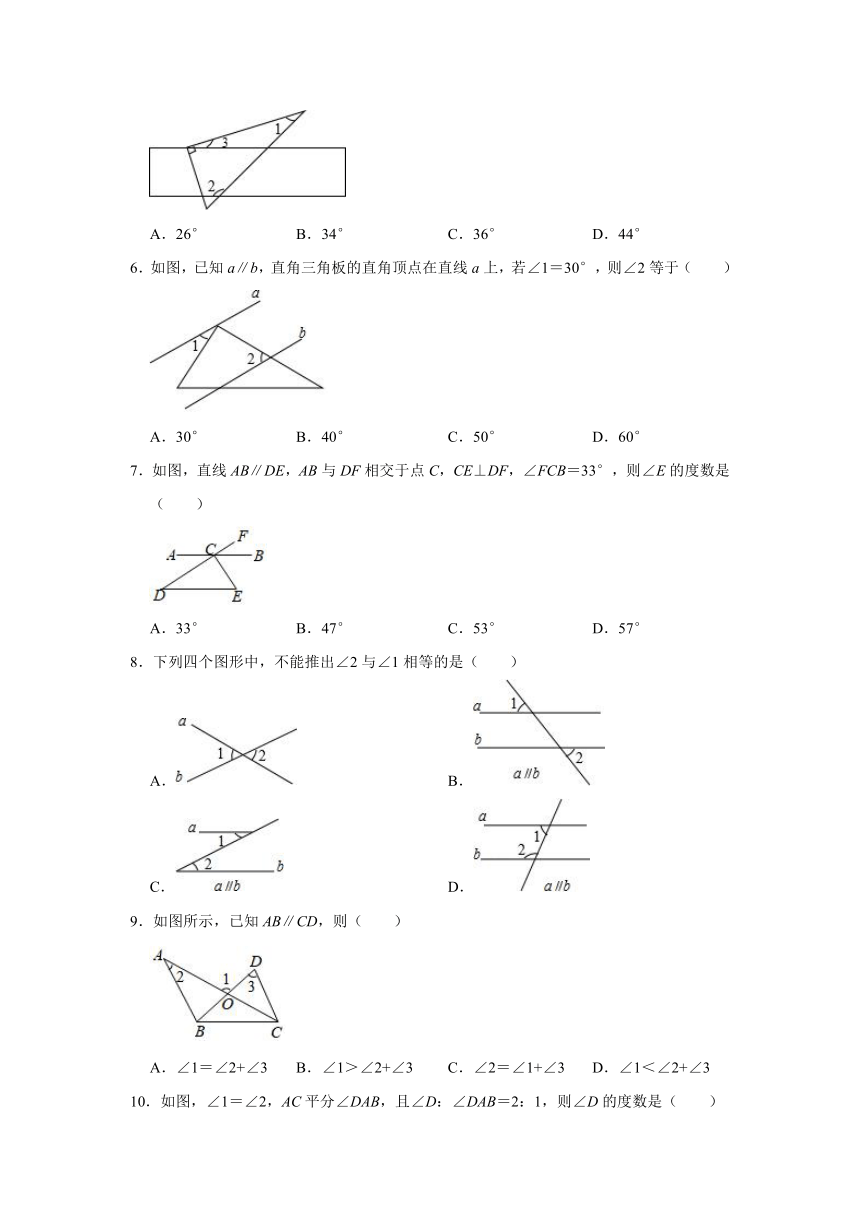
5.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=114°,则∠3的度数为( )
A.26°
B.34°
C.36°
D.44°
6.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30°
B.40°
C.50°
D.60°
7.如图,直线AB∥DE,AB与DF相交于点C,CE⊥DF,∠FCB=33°,则∠E的度数是( )
A.33°
B.47°
C.53°
D.57°
8.下列四个图形中,不能推出∠2与∠1相等的是( )
A.
B.
C.
D.
9.如图所示,已知AB∥CD,则( )
A.∠1=∠2+∠3
B.∠1>∠2+∠3
C.∠2=∠1+∠3
D.∠1<∠2+∠3
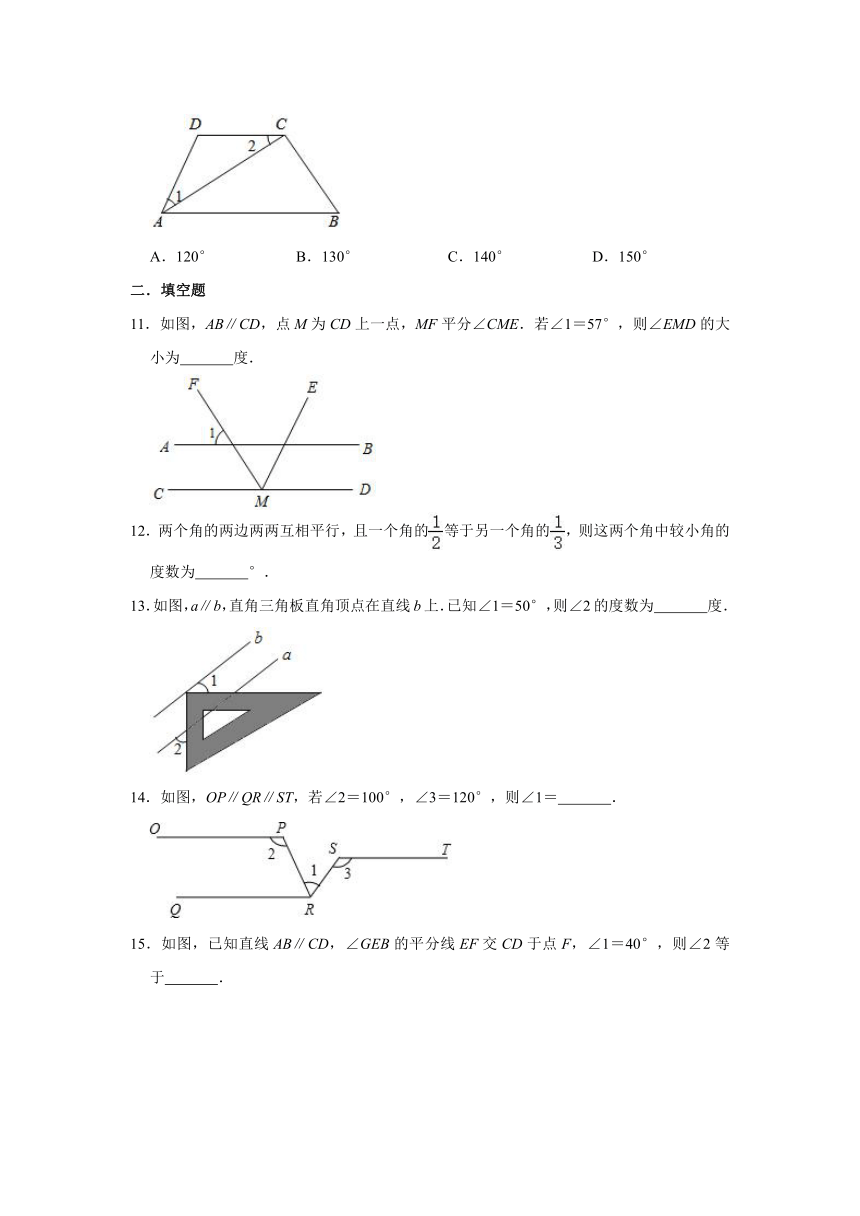
10.如图,∠1=∠2,AC平分∠DAB,且∠D:∠DAB=2:1,则∠D的度数是( )
A.120°
B.130°
C.140°
D.150°
二.填空题
11.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为
度.
12.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为
°.
13.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为
度.
14.如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=
.
15.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于
.
三.解答题
16.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
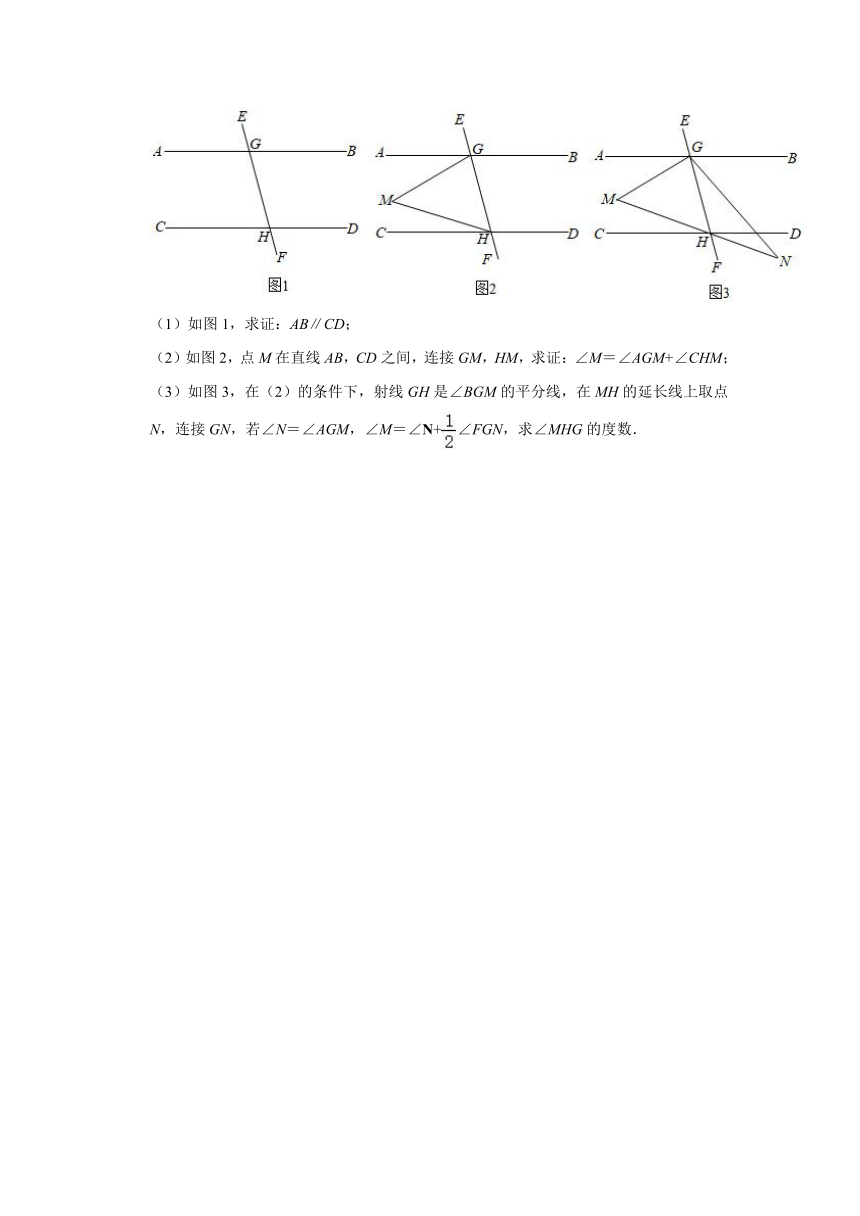
17.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
18.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
参考答案
一.选择题
1.解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
2.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
3.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
4.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
5.解:∵AB∥CD,
∴∠ABE=∠2=114°,
在△ABE中,∠3=180°﹣∠1﹣∠ABE=180°﹣30°﹣114°=36°.
故选:C.
6.解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
7.解:∵AB∥DE,∠FCB=33°,
∴∠D=∠FCB=33°,
又∵CE⊥DF,
∴∠DCE=90°,
∴∠D+∠E=90°,
则∠E=90°﹣∠D=57°,
故选:D.
8.解:A、∵∠1和∠2互为对顶角,
∴∠1=∠2,故本选项不合题意;
B、如图,∵a∥b,
∴∠1=∠3(两直线平行,同位角相等),
∵∠2=∠3(对顶角相等),
∴∠1=∠2,故本选项不合题意;
C、∵a∥b,
∴∠1=∠2(两直线平行,内错角相等),故本选项不合题意;
D、∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
不能判断∠1=∠2,故本选项符合题意;
故选:D.
9.解:∵AB∥CD,
∴∠2=∠4,
∵∠1=∠3+∠4,
∴∠1=∠3+∠2,
故选:A.
10.解:∵AC平分∠DAB,
∴∠1=∠CAB,
∵∠1=∠2,
∴∠CAB=∠2,
∴DC∥AB,
∴∠D+∠DAB=180°,
又∵∠D:∠DAB=2:1,
∴∠D=180°×=120°,
故选:A.
二.填空题
11.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
12.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
14.解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
15.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
三.解答题
16.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
17.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
18.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
同步测试
一.选择题
1.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
2.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75°
B.60°
C.45°
D.30°
3.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80°
B.90°
C.100°
D.110°
4.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40°
B.45°
C.50°
D.60°
5.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=114°,则∠3的度数为( )
A.26°
B.34°
C.36°
D.44°
6.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30°
B.40°
C.50°
D.60°
7.如图,直线AB∥DE,AB与DF相交于点C,CE⊥DF,∠FCB=33°,则∠E的度数是( )
A.33°
B.47°
C.53°
D.57°
8.下列四个图形中,不能推出∠2与∠1相等的是( )
A.
B.
C.
D.
9.如图所示,已知AB∥CD,则( )
A.∠1=∠2+∠3
B.∠1>∠2+∠3
C.∠2=∠1+∠3
D.∠1<∠2+∠3
10.如图,∠1=∠2,AC平分∠DAB,且∠D:∠DAB=2:1,则∠D的度数是( )
A.120°
B.130°
C.140°
D.150°
二.填空题
11.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为
度.
12.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为
°.
13.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为
度.
14.如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=
.
15.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于
.
三.解答题
16.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
17.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
18.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
参考答案
一.选择题
1.解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
2.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
3.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
4.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
5.解:∵AB∥CD,
∴∠ABE=∠2=114°,
在△ABE中,∠3=180°﹣∠1﹣∠ABE=180°﹣30°﹣114°=36°.
故选:C.
6.解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
7.解:∵AB∥DE,∠FCB=33°,
∴∠D=∠FCB=33°,
又∵CE⊥DF,
∴∠DCE=90°,
∴∠D+∠E=90°,
则∠E=90°﹣∠D=57°,
故选:D.
8.解:A、∵∠1和∠2互为对顶角,
∴∠1=∠2,故本选项不合题意;
B、如图,∵a∥b,
∴∠1=∠3(两直线平行,同位角相等),
∵∠2=∠3(对顶角相等),
∴∠1=∠2,故本选项不合题意;
C、∵a∥b,
∴∠1=∠2(两直线平行,内错角相等),故本选项不合题意;
D、∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
不能判断∠1=∠2,故本选项符合题意;
故选:D.
9.解:∵AB∥CD,
∴∠2=∠4,
∵∠1=∠3+∠4,
∴∠1=∠3+∠2,
故选:A.
10.解:∵AC平分∠DAB,
∴∠1=∠CAB,
∵∠1=∠2,
∴∠CAB=∠2,
∴DC∥AB,
∴∠D+∠DAB=180°,
又∵∠D:∠DAB=2:1,
∴∠D=180°×=120°,
故选:A.
二.填空题
11.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
12.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
14.解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
15.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
三.解答题
16.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
17.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
18.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
