苏科版七年级数学下册7.4认识三角形 复习教案
文档属性
| 名称 | 苏科版七年级数学下册7.4认识三角形 复习教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览




文档简介
图形的平移和认识三角形
【教学目标】
1.掌握平移的概念、基本性质,会进行平移作图
2.掌握三角形的有关概念及根据相关概念进行三角形的分类
3.掌握三角形的三边关系,掌握三角形中3条重要线段的概念、作图及性质的简单应用
【知识链接】
一.图形的平移
1.定义:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
2.平移的要素:
(1)平移的方向:原图上的点指向它的对应点的射线方向;
(2)平移的距离:连接原图与平移后图形上的一对对应点的线段的长度.
3.平移的基本性质:
(1)平移不改变图形的大小与形状,只改变图形的位置;
(2)平移后的图形与原来的图形的对应线段平行(或在同一条直线上)且相等,对应角相等;
(3)一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
二.三角形
1.定义:由3条不在同一直线上的线段,首尾依次相接组成的图形称为三角形。如图就是一个三角形。
2.三角形的各组成部分
边:组成三角形的三条线段。
如右所示:线段AB、AC、BC就是三角形的三条边。
顶点:三角形任意两边的交点。
如右所示:点A、B、C均为三角形的顶点。
通常情况下,我们用三角形的三个顶点加以一个“△”来表示一个三角形,在表示三角形时,三个字母之间并无顺序关系,如上图中,此三角形可以表示为△ABC,或△ACB或△BAC等等。
内角:三角形两边所夹的角,称为三角形的内角,简称角。
例如△ABC中,∠A,∠B,∠C都是三角形的内角,边BC称为∠A所对的边,或顶点A所对的边,因此边BC也可以表示为a,那么边AB,AC呢?
3.三角形的分类
(1)按角分:
(2)按边分:
4.三角形任意两边之和大于第三边,任意两边之差小于第三边。
5.三角形的高的定义:在三角形中,从一个顶点向它的对边所在的直线做垂线,顶点与垂足之间的线段称为三角形的高。
注:(1)三角形的高必为线段;
(2)三角形的高必过顶点垂直于对边;
(3)三角形有三条高。
6.三角形的角平分线的定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段称为三角形的角平分线。
注:(1)三角形的角平分线必为线段,而一个角的角平分线为一条射线;
(2)三角形的角平分线必过顶点平分三角形的一内角;
(3)三角形有三条角平分线。
7.三角形的中线的定义:在三角形中,连结一个顶点与它对边中点的线段,叫做三角形的中线。
注:(1)三角形的中线必为线段;
三角形的中线必平分对边;
三角形有三条中线。
知识点一:平移的定义和基本性质
【例题1】在以下现象中:①用打气筒打气时,气筒里活塞的运动;②直线传送带上,瓶装饮料的移动;③在平直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动;⑥摇动的大绳;⑦从楼顶自由落下的球(球不旋转);⑦属于平移的有(
)
A.1个
B.2个
C.3个
D.4个
【变式1】对于平移后,对应点所连的线段,下列说法正确的是
(
)
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③
B.②③
C.③④
D.①②
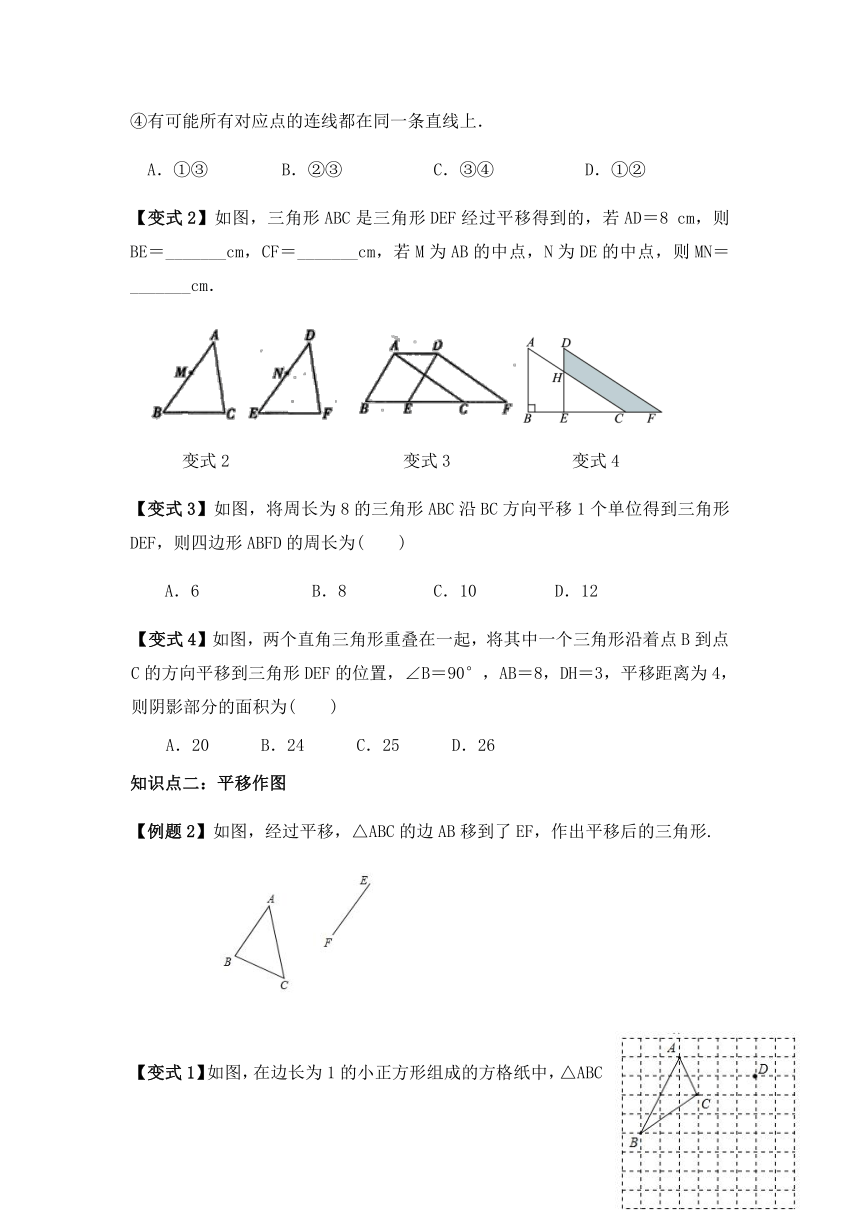
【变式2】如图,三角形ABC是三角形DEF经过平移得到的,若AD=8
cm,则BE=_______cm,CF=_______cm,若M为AB的中点,N为DE的中点,则MN=_______cm.
变式2
变式3
变式4
【变式3】如图,将周长为8的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为(
)
A.6
B.8
C.10
D.12
【变式4】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,则阴影部分的面积为( )
A.20
B.24
C.25
D.26
知识点二:平移作图
【例题2】如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.
【变式1】如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点A移到了点D的位置.
画出平移后的△DEF;(点E与点B对应,点F和点C对应)
指出平移的方向和平移的距离.
【变式2】如图,在方格纸中,每个小正方形的边长均为1个单位长度,有一个△ABC,它的三个顶点均与小正方形的顶点重合.
在△ABC向左平移4个单位长度,得到△DEF(A与D,B与E,C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和AF,请计算△AEF的面积S.
【变式3】在5×13的正方形网格中,点A、B、C、P都在格点上.
(1)将△ABC沿着射线BC方向平移得到△A1B1C1,且A1C1经过点P,画出△A1B1C1;
(2)将△ABC沿着射线BC方向平移m个单位得到△A2B2C2,此时点P落在△A2B2C2的内部,直接写出m的取值范围.
知识点三:三角形的有关概念与分类
【例题3】以下是由四位同学描述三角形的四种不同的说法,正确的是
(
)
A.由三个角组成的图形叫三角形
B.由三条线段组成的图形叫三角形
C.由三条直线组成的图形叫三角形
D.由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
【变式1】如图,点D在AB上.
(1)图中共有________个三角形,它们分别是______________;
(2)∠ABC是△ABC的内角,也是△________的内角;
(3)CD是△ACD中∠________的对边,也是△BCD中∠________的对边,也是△________和△BCD的公共边;
(4)在△ACD中,AD和CD两边所夹的角是∠________,∠BCD是△________中CB和________两边所夹的角.
【变式2】下列说法正确的是(
)
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
知识点四:三角形的三边关系
【例题4】下列各组数中,不可能作为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
【变式1】有两根长度分别为4㎝和7㎝的木棒,
用长度为2
㎝的木棒能与它们组成三角形吗?为什么?用长度为11㎝的木棒呢?
第三边在什么范围内?
(3)如果第三边是奇数,那么第三边可能是哪几个数?
(4)如果周长是奇数,那么第三边可能是哪几个数?
【变式2】下列各项中,给出的三条线段不能组成三角形的是(
)
A.a+1,a+3,a+2(a>0)
B.三边之比为5:6:10
C.30cm,8cm,10cm
D.a=2m,b=3m.c=5m-1(m>1)
【变式3】在△ABC中,三边长分别为a,b,c,已知a,b,c都是整数且b>a>c,b=5,则满足条件的三角形的个数为( )
A.2
B.3
C.4
D.5
【变式4】已知a,b,c是三角形的三边长,试化简:|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|.
知识点5:三角形中3条重要的线段
【例题5】如图,在△ABC中,AB=13,AC=10,AD为中线,则△ABD与△ACD的周长之差=________.
【变式1】有一块三角形优良品种实验田,如图,现引进四个良种进行对比实验,将这块土地分成面积相等的四块,请你定出两种划分方案,画图说明.
【变式2】在如图所示的三个三角形中,画出过顶点A的中线和高.
【变式3】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C﹣∠B=30°,则∠DAE=
.
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
【当堂练习】
1.如图,三角形ABC沿BC方向平移得到三角形DEF,CE=2,CF=4,则平移的距离是________.
第1题
第2题
2.如图,△ABC的面积为10,BC=4,现将△ABC沿着射线BC平移a个单位(a>0),得到新的△A'B'C',则△ABC所扫过的面积为_________.
3.已知三角形ABC三边a、b、c满足,则△ABC的形状是(
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
4.三角形的边长都是整数,并且唯一的最长边是6,则这样的三角形共(
)
A.
3个
B.
5个
C.
6个
D.
7个
5.已知三角形的三边长分别为a,b,c,化简|a﹣b+c|﹣|a﹣b﹣c|得( )
A.2a﹣2b
B.2a﹣2c
C.a﹣2b
D.0
6.如图,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线。
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高。
【课后作业】
1.三角形的角平分线、中线和高( )
A.都是射线
B.都是直线
C.都是线段
D.都在三角形内
2.下列现象:
(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;
(3)健身做呼啦圈运动;
(4)火车飞驰在一段平直的铁轨上.
其中属于平移的是________.(填序号)
3.在三角形ABC中,AB=5
cm,∠B=72?,若将三角形ABC向下平移7
cm得到三角形A'B'C',则A'B'=______
cm,AA'=______cm,∠B'=______?.
4.长度分别为2,7,x的三条线段能组成一个三角形,则x的值可以是( )
A.4
B.5
C.6
D.9
5.如图,将直角梯形ABCD(AB∥CD)沿射线AD平移到直角梯形EFGH的位置.若HG=10,MC=2,MG=5,求图中阴影部分的面积.
6.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
【教学目标】
1.掌握平移的概念、基本性质,会进行平移作图
2.掌握三角形的有关概念及根据相关概念进行三角形的分类
3.掌握三角形的三边关系,掌握三角形中3条重要线段的概念、作图及性质的简单应用
【知识链接】
一.图形的平移
1.定义:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
2.平移的要素:
(1)平移的方向:原图上的点指向它的对应点的射线方向;
(2)平移的距离:连接原图与平移后图形上的一对对应点的线段的长度.
3.平移的基本性质:
(1)平移不改变图形的大小与形状,只改变图形的位置;
(2)平移后的图形与原来的图形的对应线段平行(或在同一条直线上)且相等,对应角相等;
(3)一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
二.三角形
1.定义:由3条不在同一直线上的线段,首尾依次相接组成的图形称为三角形。如图就是一个三角形。
2.三角形的各组成部分
边:组成三角形的三条线段。
如右所示:线段AB、AC、BC就是三角形的三条边。
顶点:三角形任意两边的交点。
如右所示:点A、B、C均为三角形的顶点。
通常情况下,我们用三角形的三个顶点加以一个“△”来表示一个三角形,在表示三角形时,三个字母之间并无顺序关系,如上图中,此三角形可以表示为△ABC,或△ACB或△BAC等等。
内角:三角形两边所夹的角,称为三角形的内角,简称角。
例如△ABC中,∠A,∠B,∠C都是三角形的内角,边BC称为∠A所对的边,或顶点A所对的边,因此边BC也可以表示为a,那么边AB,AC呢?
3.三角形的分类
(1)按角分:
(2)按边分:
4.三角形任意两边之和大于第三边,任意两边之差小于第三边。
5.三角形的高的定义:在三角形中,从一个顶点向它的对边所在的直线做垂线,顶点与垂足之间的线段称为三角形的高。
注:(1)三角形的高必为线段;
(2)三角形的高必过顶点垂直于对边;
(3)三角形有三条高。
6.三角形的角平分线的定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段称为三角形的角平分线。
注:(1)三角形的角平分线必为线段,而一个角的角平分线为一条射线;
(2)三角形的角平分线必过顶点平分三角形的一内角;
(3)三角形有三条角平分线。
7.三角形的中线的定义:在三角形中,连结一个顶点与它对边中点的线段,叫做三角形的中线。
注:(1)三角形的中线必为线段;
三角形的中线必平分对边;
三角形有三条中线。
知识点一:平移的定义和基本性质
【例题1】在以下现象中:①用打气筒打气时,气筒里活塞的运动;②直线传送带上,瓶装饮料的移动;③在平直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动;⑥摇动的大绳;⑦从楼顶自由落下的球(球不旋转);⑦属于平移的有(
)
A.1个
B.2个
C.3个
D.4个
【变式1】对于平移后,对应点所连的线段,下列说法正确的是
(
)
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③
B.②③
C.③④
D.①②
【变式2】如图,三角形ABC是三角形DEF经过平移得到的,若AD=8
cm,则BE=_______cm,CF=_______cm,若M为AB的中点,N为DE的中点,则MN=_______cm.
变式2
变式3
变式4
【变式3】如图,将周长为8的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为(
)
A.6
B.8
C.10
D.12
【变式4】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,则阴影部分的面积为( )
A.20
B.24
C.25
D.26
知识点二:平移作图
【例题2】如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.
【变式1】如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点A移到了点D的位置.
画出平移后的△DEF;(点E与点B对应,点F和点C对应)
指出平移的方向和平移的距离.
【变式2】如图,在方格纸中,每个小正方形的边长均为1个单位长度,有一个△ABC,它的三个顶点均与小正方形的顶点重合.
在△ABC向左平移4个单位长度,得到△DEF(A与D,B与E,C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和AF,请计算△AEF的面积S.
【变式3】在5×13的正方形网格中,点A、B、C、P都在格点上.
(1)将△ABC沿着射线BC方向平移得到△A1B1C1,且A1C1经过点P,画出△A1B1C1;
(2)将△ABC沿着射线BC方向平移m个单位得到△A2B2C2,此时点P落在△A2B2C2的内部,直接写出m的取值范围.
知识点三:三角形的有关概念与分类
【例题3】以下是由四位同学描述三角形的四种不同的说法,正确的是
(
)
A.由三个角组成的图形叫三角形
B.由三条线段组成的图形叫三角形
C.由三条直线组成的图形叫三角形
D.由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
【变式1】如图,点D在AB上.
(1)图中共有________个三角形,它们分别是______________;
(2)∠ABC是△ABC的内角,也是△________的内角;
(3)CD是△ACD中∠________的对边,也是△BCD中∠________的对边,也是△________和△BCD的公共边;
(4)在△ACD中,AD和CD两边所夹的角是∠________,∠BCD是△________中CB和________两边所夹的角.
【变式2】下列说法正确的是(
)
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
知识点四:三角形的三边关系
【例题4】下列各组数中,不可能作为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
【变式1】有两根长度分别为4㎝和7㎝的木棒,
用长度为2
㎝的木棒能与它们组成三角形吗?为什么?用长度为11㎝的木棒呢?
第三边在什么范围内?
(3)如果第三边是奇数,那么第三边可能是哪几个数?
(4)如果周长是奇数,那么第三边可能是哪几个数?
【变式2】下列各项中,给出的三条线段不能组成三角形的是(
)
A.a+1,a+3,a+2(a>0)
B.三边之比为5:6:10
C.30cm,8cm,10cm
D.a=2m,b=3m.c=5m-1(m>1)
【变式3】在△ABC中,三边长分别为a,b,c,已知a,b,c都是整数且b>a>c,b=5,则满足条件的三角形的个数为( )
A.2
B.3
C.4
D.5
【变式4】已知a,b,c是三角形的三边长,试化简:|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|.
知识点5:三角形中3条重要的线段
【例题5】如图,在△ABC中,AB=13,AC=10,AD为中线,则△ABD与△ACD的周长之差=________.
【变式1】有一块三角形优良品种实验田,如图,现引进四个良种进行对比实验,将这块土地分成面积相等的四块,请你定出两种划分方案,画图说明.
【变式2】在如图所示的三个三角形中,画出过顶点A的中线和高.
【变式3】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C﹣∠B=30°,则∠DAE=
.
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
【当堂练习】
1.如图,三角形ABC沿BC方向平移得到三角形DEF,CE=2,CF=4,则平移的距离是________.
第1题
第2题
2.如图,△ABC的面积为10,BC=4,现将△ABC沿着射线BC平移a个单位(a>0),得到新的△A'B'C',则△ABC所扫过的面积为_________.
3.已知三角形ABC三边a、b、c满足,则△ABC的形状是(
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
4.三角形的边长都是整数,并且唯一的最长边是6,则这样的三角形共(
)
A.
3个
B.
5个
C.
6个
D.
7个
5.已知三角形的三边长分别为a,b,c,化简|a﹣b+c|﹣|a﹣b﹣c|得( )
A.2a﹣2b
B.2a﹣2c
C.a﹣2b
D.0
6.如图,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线。
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高。
【课后作业】
1.三角形的角平分线、中线和高( )
A.都是射线
B.都是直线
C.都是线段
D.都在三角形内
2.下列现象:
(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;
(3)健身做呼啦圈运动;
(4)火车飞驰在一段平直的铁轨上.
其中属于平移的是________.(填序号)
3.在三角形ABC中,AB=5
cm,∠B=72?,若将三角形ABC向下平移7
cm得到三角形A'B'C',则A'B'=______
cm,AA'=______cm,∠B'=______?.
4.长度分别为2,7,x的三条线段能组成一个三角形,则x的值可以是( )
A.4
B.5
C.6
D.9
5.如图,将直角梯形ABCD(AB∥CD)沿射线AD平移到直角梯形EFGH的位置.若HG=10,MC=2,MG=5,求图中阴影部分的面积.
6.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
