人教版八年级数学下上册第12章 全等三角形的性质与判定复习学案(无答案)
文档属性
| 名称 | 人教版八年级数学下上册第12章 全等三角形的性质与判定复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 351.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:01:57 | ||
图片预览



文档简介
第一节
全等三角形的性质与判定
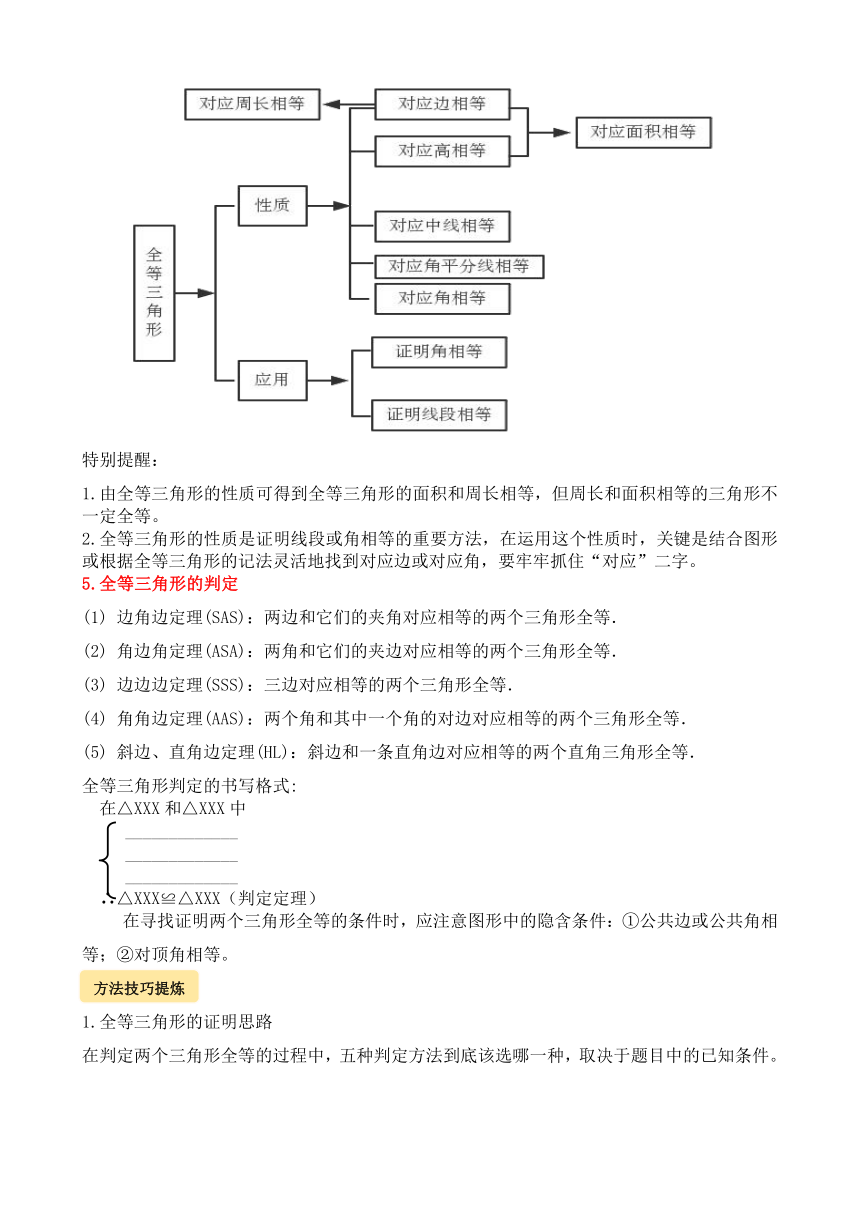
1.全等三角形的有关概念
全等图形:能够完全重合的两个图形叫做全等图形。
注:平移、对称、旋转前后的图形全等。
全等三角形:能够完全重合的两个三角形叫做全等三角形。
相关概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
2.表示方法:△ABC和△DEF全等,记作△ABC≌△DEF,读作“三角形ABC全等于三角形DEF”。
注:书写全等三角形时要求对应顶点必须写在对应位置。
3.全等三角形的一般规律
⑴全等三角形对应角所对的边是对应边,两组对应角所夹的边是对应边;
⑵全等三角形对应边所对的角是对应角,两组对应边所夹的角是对应角;
⑶两个全等三角形中的一对最长边(最大角)是对应边(对应角),一对最短边(最小角)是对应边(对应角);
⑷两个全等三角形有公共边时,公共边是对应边;
⑸两个全等三角形有公共角时,公共角是对应角;
⑹两个全等三角形有对顶角时,对顶角是对应角。
4.全等三角形的性质
特别提醒:
1.由全等三角形的性质可得到全等三角形的面积和周长相等,但周长和面积相等的三角形不一定全等。
2.全等三角形的性质是证明线段或角相等的重要方法,在运用这个性质时,关键是结合图形或根据全等三角形的记法灵活地找到对应边或对应角,要牢牢抓住“对应”二字。
5.全等三角形的判定
(1)
边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.
(2)
角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.
(3)
边边边定理(SSS):三边对应相等的两个三角形全等.
(4)
角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.
(5)
斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
全等三角形判定的书写格式:
在△XXX和△XXX中
_____________
_____________
_____________
∴△XXX≌△XXX(判定定理)
在寻找证明两个三角形全等的条件时,应注意图形中的隐含条件:①公共边或公共角相等;②对顶角相等。
1.全等三角形的证明思路
在判定两个三角形全等的过程中,五种判定方法到底该选哪一种,取决于题目中的已知条件。
2.证明全等三角形的对应角相等的思路
(1)平行线性质
(2)外角定理
(3)同角(等角)的余角(补角)相等
(4)同角(等角)加减公共角。
3.证明角度相等的方法
⑴对顶尖相等;⑵平行线性质;⑶外角定理;⑷同角(等角)的余角(补角)相等;⑸等角加减公共角;⑹证明两个角所在的两个三角形全等。
4.证明线段相等的方法
⑴等量代换;⑵等边加减公共边(等边);⑶面积法:若两个三角形面积相等,底等则高等(高等则底等);⑷证明两条线段所在的两个三角形全等。
例题1-1.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,
∠F=40°
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长。
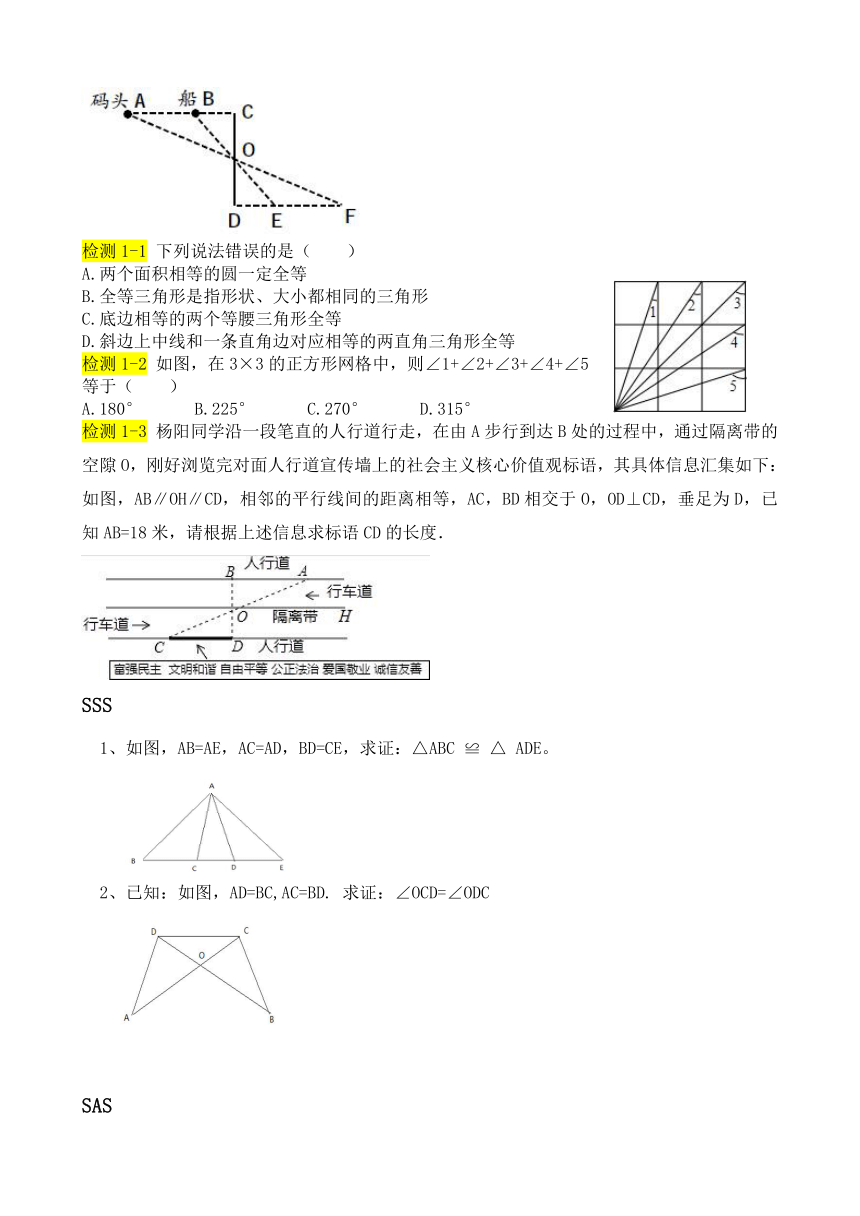
例题1-2.小强在河的一边,要测河面一只船B与对岸码头A的距离,他的做法如下:①在岸边确定一点C,使C与A,B在同一直线上;②在AC的垂直方向画线段CD,取其中点O;③画DF⊥CD,使F,O,A在同一直线上;④在线段DF上找到一点E,使E与O,B共线.他说只要测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
检测1-1
下列说法错误的是(
)
A.两个面积相等的圆一定全等
B.全等三角形是指形状、大小都相同的三角形?
C.底边相等的两个等腰三角形全等
D.斜边上中线和一条直角边对应相等的两直角三角形全等
检测1-2
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
A.180°
B.225°
C.270°
D.315°
检测1-3
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB∥OH∥CD,相邻的平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=18米,请根据上述信息求标语CD的长度.?
SSS
1、如图,AB=AE,AC=AD,BD=CE,求证:△ABC
≌
△
ADE。
2、已知:如图,AD=BC,AC=BD.
求证:∠OCD=∠ODC
SAS
1、如图,AC=BD,∠1=
∠2,求证:BC=AD.
2、如图,AC=BD,BC=AD,求证:∠C=∠D
3、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD(允许添加一个条件)
4、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
AAS
ASA
1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
2、已知:点D在AB上,点E在AC上,∠BAO=∠CAO
,BE⊥AC,CD⊥AB,相交于点O,AB=AC,求证:BD=CE
3、如图,在△ABC中,∠C=2∠B、,AD是△ABC的角平分线,∠1=∠B,求证AB=AC+CD
HL
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什关系?
如图,△ABC中,AB=AC,AD是高,证明△ADB与△ADC全等
4、判断两个直角三角形全等的方法不正确的有(
)
A、两条直角边对应相等
B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等
D、两个锐角对应相等
5、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
6、如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。
求证:MB=MD,ME=MF;
(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
7、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
1.下列说法中,错误的是(
)
①只有两个三角形才能完全重合;②如果两个图形是全等形,那么它们的形状和大小一定都相同;③两个正方形一定是全等形;④边数相同的图形一定能互相重合.
A.①③④
B.①②③
C.①③
D.①④
2.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有????.
3.如图,正方形①,②的一边在同一直线上,正方形③的一个顶点也在该直线上,且有两个顶点分别与正方形①,②的两个顶点重合,若正方形①,②的面积分别3cm?和4cm?,则正方形③③的面积为
______cm?
4.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(????)
5.在铁路线CD附近有两个村庄A、B,到铁路的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C、D,且CD=25km.现在要在铁路线旁建一个农副产品收购站E,使A、B两村到E站的距离相等,你知道应该把E站建在距点C多少千米的地方吗?
全等三角形好题归纳举例
知识提要
1、判断全等三角形的方法有:①__________;②___________;③___________;
④__________;⑤___________。就是没有SSA.
2、全等三角形有哪些性质:①___________________;②________________.
二、讲练结合
1.如图,AC=BD,AB=DC,求证:∠B=∠C.
变式
精练:如图AB=AC,BD=CD,求证:∠B=∠C.
2.如图,AB=AD,CD=CB,∠A+∠C=180°,试探索CB与AB的位置关系.
变式(一)精练:如图,AC=AB,BD=CD,AD与BC相交于O,求证:AD⊥BC.
变式(二)精练:在△ABC中,分别以AB、AC为边在△ABC的外面作正△ABE和正△ACF,求证:BF=CE.
3.如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
变式
精练:如图,AB=AE,∠B=∠E,∠BAC=∠EAD,∠CAF=∠DAF,求证:AF⊥CD.
4.已知AB是等腰直角三角形ABC的斜边,AD是∠BAC的角平分线,求证:AC+CD=AB.
变式
精练:已知E是AD上的一点,AB=AC,AE=BD,CE=BD+DE,求证:∠B=∠CAD.
5.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,
求证:DE=AD-BE.
变式
精练:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
6.如图,AD是△ABC的高,∠B=2∠C,求证:CD=AB+BD.
7.在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,使BD=CE,连结DE交BC于F,求证:DF=EF.
变式
精练:在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,连结DE交BC于F,若DF=EF,求证:BD=CE.
8.如图,OA=OB,C、D分别是OA,OB上的两点,且OC=OD,连结AD、BC交于E,求证:OE平分∠AOB.
变式
精练:如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF.
日期:_______
姓名:
1.下列说法中,正确的是(
)
A.斜边对应相等的两个直角三角形全等
B.底边对应相等的两个等腰三角形全等
C.面积相等的两个等边三角形全等?
D.面积相等的两个长方形全等
2.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是(
)
A.球
B.圆柱
C.三棱柱
D.圆锥
3.如图,四个全等的小正方形拼成一个大正方形,则此图中∠1+∠2+∠3=????度.
4.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有????.
5.如图,点B,E,C,F在同一条直线上,AB=DE,∠B=∠DEF.要使△ABC≌△DEF,则需要再添加的一个条件是_________.(写出一个即可)
全等三角形的性质与判定
1.全等三角形的有关概念
全等图形:能够完全重合的两个图形叫做全等图形。
注:平移、对称、旋转前后的图形全等。
全等三角形:能够完全重合的两个三角形叫做全等三角形。
相关概念:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
2.表示方法:△ABC和△DEF全等,记作△ABC≌△DEF,读作“三角形ABC全等于三角形DEF”。
注:书写全等三角形时要求对应顶点必须写在对应位置。
3.全等三角形的一般规律
⑴全等三角形对应角所对的边是对应边,两组对应角所夹的边是对应边;
⑵全等三角形对应边所对的角是对应角,两组对应边所夹的角是对应角;
⑶两个全等三角形中的一对最长边(最大角)是对应边(对应角),一对最短边(最小角)是对应边(对应角);
⑷两个全等三角形有公共边时,公共边是对应边;
⑸两个全等三角形有公共角时,公共角是对应角;
⑹两个全等三角形有对顶角时,对顶角是对应角。
4.全等三角形的性质
特别提醒:
1.由全等三角形的性质可得到全等三角形的面积和周长相等,但周长和面积相等的三角形不一定全等。
2.全等三角形的性质是证明线段或角相等的重要方法,在运用这个性质时,关键是结合图形或根据全等三角形的记法灵活地找到对应边或对应角,要牢牢抓住“对应”二字。
5.全等三角形的判定
(1)
边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.
(2)
角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.
(3)
边边边定理(SSS):三边对应相等的两个三角形全等.
(4)
角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.
(5)
斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
全等三角形判定的书写格式:
在△XXX和△XXX中
_____________
_____________
_____________
∴△XXX≌△XXX(判定定理)
在寻找证明两个三角形全等的条件时,应注意图形中的隐含条件:①公共边或公共角相等;②对顶角相等。
1.全等三角形的证明思路
在判定两个三角形全等的过程中,五种判定方法到底该选哪一种,取决于题目中的已知条件。
2.证明全等三角形的对应角相等的思路
(1)平行线性质
(2)外角定理
(3)同角(等角)的余角(补角)相等
(4)同角(等角)加减公共角。
3.证明角度相等的方法
⑴对顶尖相等;⑵平行线性质;⑶外角定理;⑷同角(等角)的余角(补角)相等;⑸等角加减公共角;⑹证明两个角所在的两个三角形全等。
4.证明线段相等的方法
⑴等量代换;⑵等边加减公共边(等边);⑶面积法:若两个三角形面积相等,底等则高等(高等则底等);⑷证明两条线段所在的两个三角形全等。
例题1-1.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,
∠F=40°
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长。
例题1-2.小强在河的一边,要测河面一只船B与对岸码头A的距离,他的做法如下:①在岸边确定一点C,使C与A,B在同一直线上;②在AC的垂直方向画线段CD,取其中点O;③画DF⊥CD,使F,O,A在同一直线上;④在线段DF上找到一点E,使E与O,B共线.他说只要测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
检测1-1
下列说法错误的是(
)
A.两个面积相等的圆一定全等
B.全等三角形是指形状、大小都相同的三角形?
C.底边相等的两个等腰三角形全等
D.斜边上中线和一条直角边对应相等的两直角三角形全等
检测1-2
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
A.180°
B.225°
C.270°
D.315°
检测1-3
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB∥OH∥CD,相邻的平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=18米,请根据上述信息求标语CD的长度.?
SSS
1、如图,AB=AE,AC=AD,BD=CE,求证:△ABC
≌
△
ADE。
2、已知:如图,AD=BC,AC=BD.
求证:∠OCD=∠ODC
SAS
1、如图,AC=BD,∠1=
∠2,求证:BC=AD.
2、如图,AC=BD,BC=AD,求证:∠C=∠D
3、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD(允许添加一个条件)
4、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
AAS
ASA
1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
2、已知:点D在AB上,点E在AC上,∠BAO=∠CAO
,BE⊥AC,CD⊥AB,相交于点O,AB=AC,求证:BD=CE
3、如图,在△ABC中,∠C=2∠B、,AD是△ABC的角平分线,∠1=∠B,求证AB=AC+CD
HL
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什关系?
如图,△ABC中,AB=AC,AD是高,证明△ADB与△ADC全等
4、判断两个直角三角形全等的方法不正确的有(
)
A、两条直角边对应相等
B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等
D、两个锐角对应相等
5、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
6、如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。
求证:MB=MD,ME=MF;
(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
7、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
1.下列说法中,错误的是(
)
①只有两个三角形才能完全重合;②如果两个图形是全等形,那么它们的形状和大小一定都相同;③两个正方形一定是全等形;④边数相同的图形一定能互相重合.
A.①③④
B.①②③
C.①③
D.①④
2.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有????.
3.如图,正方形①,②的一边在同一直线上,正方形③的一个顶点也在该直线上,且有两个顶点分别与正方形①,②的两个顶点重合,若正方形①,②的面积分别3cm?和4cm?,则正方形③③的面积为
______cm?
4.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(????)
5.在铁路线CD附近有两个村庄A、B,到铁路的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C、D,且CD=25km.现在要在铁路线旁建一个农副产品收购站E,使A、B两村到E站的距离相等,你知道应该把E站建在距点C多少千米的地方吗?
全等三角形好题归纳举例
知识提要
1、判断全等三角形的方法有:①__________;②___________;③___________;
④__________;⑤___________。就是没有SSA.
2、全等三角形有哪些性质:①___________________;②________________.
二、讲练结合
1.如图,AC=BD,AB=DC,求证:∠B=∠C.
变式
精练:如图AB=AC,BD=CD,求证:∠B=∠C.
2.如图,AB=AD,CD=CB,∠A+∠C=180°,试探索CB与AB的位置关系.
变式(一)精练:如图,AC=AB,BD=CD,AD与BC相交于O,求证:AD⊥BC.
变式(二)精练:在△ABC中,分别以AB、AC为边在△ABC的外面作正△ABE和正△ACF,求证:BF=CE.
3.如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
变式
精练:如图,AB=AE,∠B=∠E,∠BAC=∠EAD,∠CAF=∠DAF,求证:AF⊥CD.
4.已知AB是等腰直角三角形ABC的斜边,AD是∠BAC的角平分线,求证:AC+CD=AB.
变式
精练:已知E是AD上的一点,AB=AC,AE=BD,CE=BD+DE,求证:∠B=∠CAD.
5.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,
求证:DE=AD-BE.
变式
精练:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
6.如图,AD是△ABC的高,∠B=2∠C,求证:CD=AB+BD.
7.在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,使BD=CE,连结DE交BC于F,求证:DF=EF.
变式
精练:在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,连结DE交BC于F,若DF=EF,求证:BD=CE.
8.如图,OA=OB,C、D分别是OA,OB上的两点,且OC=OD,连结AD、BC交于E,求证:OE平分∠AOB.
变式
精练:如图,AB=AC,D是∠BAC的角平分线上的一点,连结CD并延长交AB于E,连结BD并延长交AC于F,求证:AE=AF.
日期:_______
姓名:
1.下列说法中,正确的是(
)
A.斜边对应相等的两个直角三角形全等
B.底边对应相等的两个等腰三角形全等
C.面积相等的两个等边三角形全等?
D.面积相等的两个长方形全等
2.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是(
)
A.球
B.圆柱
C.三棱柱
D.圆锥
3.如图,四个全等的小正方形拼成一个大正方形,则此图中∠1+∠2+∠3=????度.
4.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有????.
5.如图,点B,E,C,F在同一条直线上,AB=DE,∠B=∠DEF.要使△ABC≌△DEF,则需要再添加的一个条件是_________.(写出一个即可)
