北师大版九年级下册第三章圆高频考点专题练习一遍过(一)(Word版,附答案)
文档属性
| 名称 | 北师大版九年级下册第三章圆高频考点专题练习一遍过(一)(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 23:56:17 | ||
图片预览


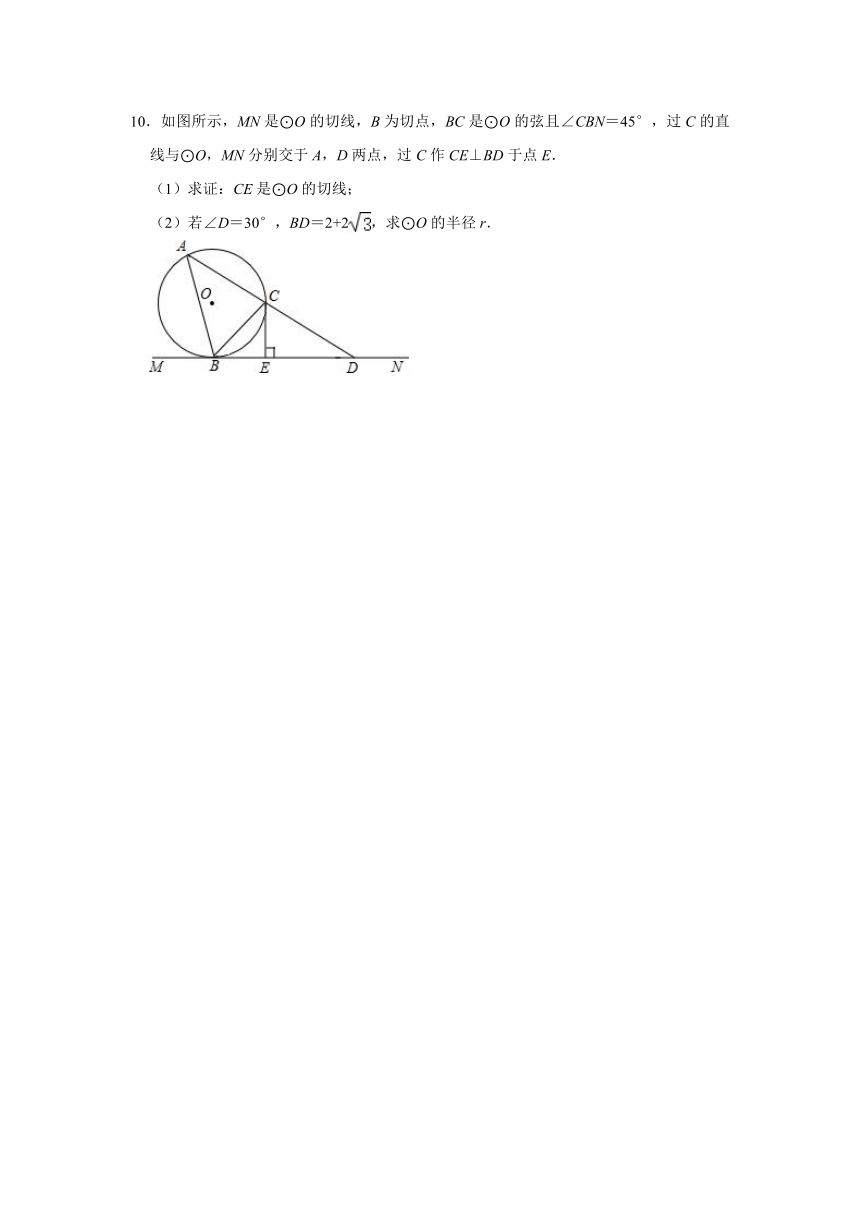

文档简介
《圆》高频考点专题练习一遍过(一)
1.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8,CD=24,求⊙O的直径.
2.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
3.已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长.
4.已知“6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B,OB与小⊙O相交于A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,设∠FOB=30°,OB=4,BC=6.
(1)求证:AD为小⊙O的切线;
(2)求DH的长.(结果保留根号)
5.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,点O在AB上,经过A、D两点的⊙O交AB于E.
(1)求证:BC是⊙O的切线;
(2)若AC=6,BC=8,求⊙O的半径.
6.如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心OB为半径的圆与AB交于点E,与AC交于点D,连接DE、DE、OC,若DE∥OC.
(1)求证:AC是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
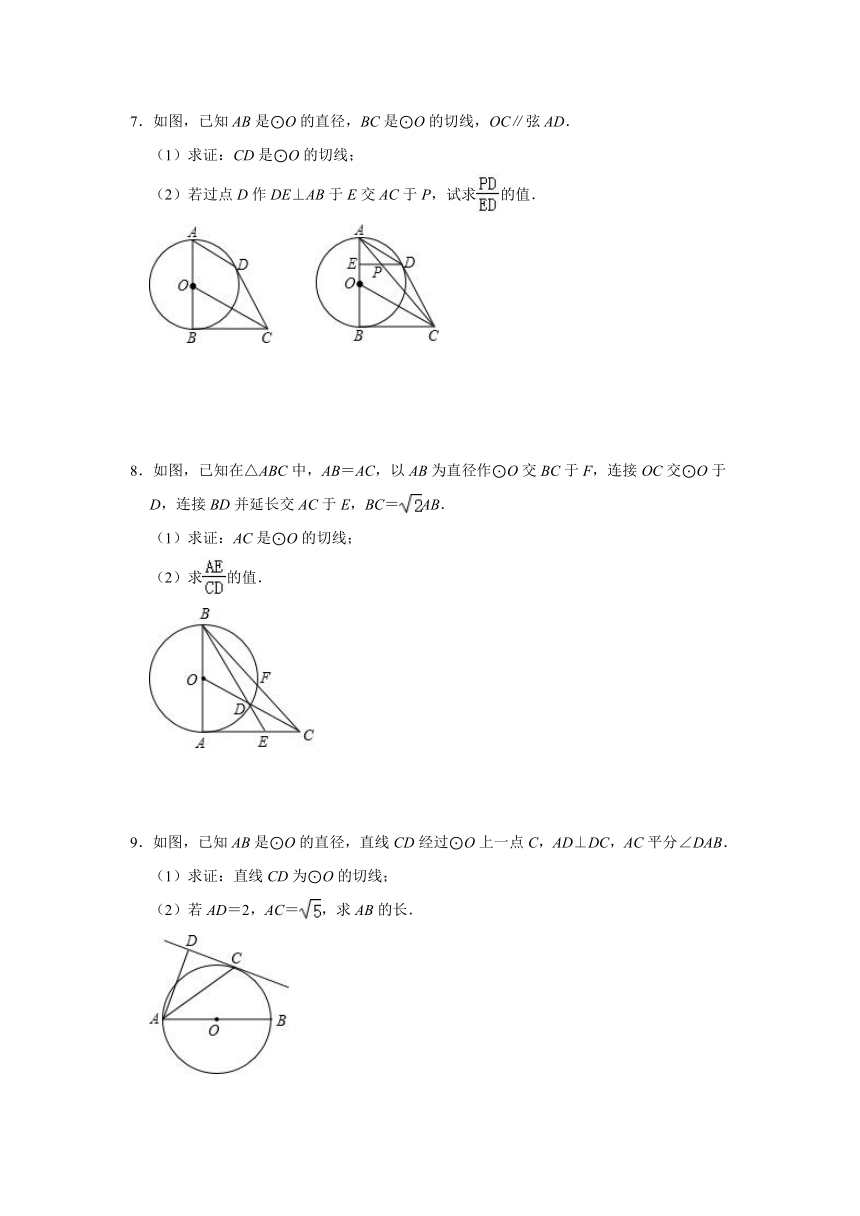
7.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD.
(1)求证:CD是⊙O的切线;
(2)若过点D作DE⊥AB于E交AC于P,试求的值.
8.如图,已知在△ABC中,AB=AC,以AB为直径作⊙O交BC于F,连接OC交⊙O于D,连接BD并延长交AC于E,BC=AB.
(1)求证:AC是⊙O的切线;
(2)求的值.
9.如图,已知AB是⊙O的直径,直线CD经过⊙O上一点C,AD⊥DC,AC平分∠DAB.
(1)求证:直线CD为⊙O的切线;
(2)若AD=2,AC=,求AB的长.
10.如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=2+2,求⊙O的半径r.
参考答案
1.(1)证明:∵AB⊥CD,
∴,
∴∠A=∠BCD,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)解:设⊙O的半径为r,则OC=r,OE=OA﹣BE=r﹣8,
∵AB⊥CD,
∴CE=DE=CD=×24=12,
在Rt△OCE中,122+(r﹣8)2=r2,解得r=13,
∴⊙O的直径=2r=26.
2.(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:在△FEA与△FBE中,
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE,
∴==,
∴AFBF=EFEF,
∴AF×(AF+15)=10×10,
解得AF=5.
∴BF=20.
∴=,
∴BE=2AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴AE2+BE2=152,
∴AE2+(2AE)2=225,
∴AE=3.
3.证明:连接OA,
(1)∵sinB=,
∴∠B=30°,
∠AOC=60°,
又∵OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∴∠OAD=60°+30°=90°,
∴AD是⊙O的切线;
(2)∵OC⊥AB,OC是半径,
∴BE=AE,
∴OD是AB的垂直平分线,
∴∠DAE=60°,∠D=30°,
在Rt△ACE中,AE=cos30°×AC=,
∴在Rt△ADE中,AD=2AE=5.
4.(1)证明:∵BC与大⊙O相切于B,
∴OB⊥BC.
∵AD∥BC,
∴OB⊥AD,即OA⊥AD,
∴AD为小⊙O的切线.
(2)解:∵AD∥BC,CD∥BH,∴四边形BCDG是平行四边形.
∴DG=BC=6.
∵∠FOB=30°,BH∥FM,
∴∠OBG=30°,∠BGA=60°=∠DGH.
在Rt△DGH中,
DH=DGsin60°=6×=3.
5.证明:(1)连接OD,(1分)
∵∠BAC的平分线AD交BC于D,
∴∠OAD=∠CAD;
又∵∠OAD=∠ODA,
∴∠ODA=∠CDA,
∴OD∥AC.
∵∠ACB=90°,
∴OD⊥BC,(3分)
∴BC是⊙O的切线.∵AC=6,BC=8,
∴AB=10;
过C作CH⊥AB于H,
则CH==,(5分)
连接OC,设⊙O的半径为r;
则S△ABC=S△OBC+S△OAC=,(6分)
∴,
∴.(8分)
6.证明:(1)连接OD,
∵DE∥OC,
∴∠DEB=∠COB,∠DOC=∠ODE.
∵∠ODE=∠OED,
∴∠DOC=∠BOC.
∵OD=OD,OC=OC,
∴∠CDO=∠CBO=90°.
∴∠ODA=90°.
∴AC是⊙O的切线.
解:(2)设半径为x,则x2+4=(x+1)2
∴x=1.5
∴AB=4.
∵BC=CD,
∴CD2+16=(CD+2)2
∴CD=3.
7.(1)证明:连接OD,BD;
∵OC∥弦AD,
∴∠BOC=∠A,∠ADO=DOC.
∵OA=OD,
∴∠A=∠COD.
∴∠COD=∠BOC.
∵OC=OC,OB=OD,
∴△OCD≌△OCB.
∴∠B=∠ODC=90°.
∴CD是⊙O的切线.
(2)解:∵BC是⊙O的切线,
∴∠OBC=90°.
∵DE⊥AB,
∴∠AED=90°.
∴∠OBC=∠AED.
∵OC∥弦AD,
∴∠BOC=∠EAD.
∴△OBC∽△AED.
∴BC:DE=OB:AE.
∵PE∥BC,
∴△ABC∽△AEP.
∴BC:EP=AB:AE.
∵AB=2OB,
∴DE=2PE.
∴PD=PE.
∴PD:ED=1:2.
8.(1)证明:连接AF,则AF⊥BC;
∵AB=AC,且AF⊥BC,
∴F是BC的中点,即CF=BC=AC;
在Rt△ACF中,AC=FC,则∠FCA=45°;
即△ABC是等腰直角三角形,故AB⊥AC,
∵AB是⊙O的直径,
∴AC是⊙O的切线.
(2)解:连接AD,则AD⊥BE;
∵∠EDC=∠ODB,而∠ODB=∠OBD,
∴∠EDC=∠OBD;
由弦切角定理知:∠DAE=∠OBD,故∠EDC=∠DAE,
易得:△CDE∽△CAD,
∴,而;
即?;
由(1)知:AB=AC,故=1.
9.证明:(1)连OC.
∵AD⊥DC,
∴∠ADC=90°.
∵AC平分∠DAB,
∴∠DAC=∠CAB.
又OC=OA,
∴∠CAB=∠ACO,
∴∠DAC=∠ACO,
∴OC∥AD.
∴∠OCD=180°﹣∠ADC=90°.
又OC是⊙O的半径,
∴CD是⊙O的切线.解:连接BC;
∵AB是⊙O的直径,
∴∠ACB=90°.
又∠ADC=90°,
∴∠ADC=∠ACB=90°,
由(1)可知∠DAC=∠CAB,
∴△ACD∽△ABC.
∴而AD=2.
∴,
∴,
故AB的长为.(8分)
10.(1)证明:连接OB、OC.
∵MN是⊙O的切线,
∴OB⊥MN.
∵∠CBN=45°,
∴∠OBC=45°,∠BCE=45°.
∵OB=OC,
∴∠OBC=∠OCB=45°.
∴∠OCE=90°,
∴CE是⊙O的切线;
(2)解:∵OB⊥BE,CE⊥BE,OC⊥CE,
∴四边形BOCE是矩形,
又OB=OC,
∴四边形BOCE是正方形,
∴BE=CE=OB=OC=r.
在Rt△CDE中,
∵∠D=30°,CE=r,
∴DE=r.
∵BD=2+2,
∴r+r=2+2,
∴r=2,即⊙O的半径为2.
1.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8,CD=24,求⊙O的直径.
2.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
3.已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长.
4.已知“6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B,OB与小⊙O相交于A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,设∠FOB=30°,OB=4,BC=6.
(1)求证:AD为小⊙O的切线;
(2)求DH的长.(结果保留根号)
5.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,点O在AB上,经过A、D两点的⊙O交AB于E.
(1)求证:BC是⊙O的切线;
(2)若AC=6,BC=8,求⊙O的半径.
6.如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心OB为半径的圆与AB交于点E,与AC交于点D,连接DE、DE、OC,若DE∥OC.
(1)求证:AC是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
7.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD.
(1)求证:CD是⊙O的切线;
(2)若过点D作DE⊥AB于E交AC于P,试求的值.
8.如图,已知在△ABC中,AB=AC,以AB为直径作⊙O交BC于F,连接OC交⊙O于D,连接BD并延长交AC于E,BC=AB.
(1)求证:AC是⊙O的切线;
(2)求的值.
9.如图,已知AB是⊙O的直径,直线CD经过⊙O上一点C,AD⊥DC,AC平分∠DAB.
(1)求证:直线CD为⊙O的切线;
(2)若AD=2,AC=,求AB的长.
10.如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=2+2,求⊙O的半径r.
参考答案
1.(1)证明:∵AB⊥CD,
∴,
∴∠A=∠BCD,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)解:设⊙O的半径为r,则OC=r,OE=OA﹣BE=r﹣8,
∵AB⊥CD,
∴CE=DE=CD=×24=12,
在Rt△OCE中,122+(r﹣8)2=r2,解得r=13,
∴⊙O的直径=2r=26.
2.(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:在△FEA与△FBE中,
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE,
∴==,
∴AFBF=EFEF,
∴AF×(AF+15)=10×10,
解得AF=5.
∴BF=20.
∴=,
∴BE=2AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴AE2+BE2=152,
∴AE2+(2AE)2=225,
∴AE=3.
3.证明:连接OA,
(1)∵sinB=,
∴∠B=30°,
∠AOC=60°,
又∵OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∴∠OAD=60°+30°=90°,
∴AD是⊙O的切线;
(2)∵OC⊥AB,OC是半径,
∴BE=AE,
∴OD是AB的垂直平分线,
∴∠DAE=60°,∠D=30°,
在Rt△ACE中,AE=cos30°×AC=,
∴在Rt△ADE中,AD=2AE=5.
4.(1)证明:∵BC与大⊙O相切于B,
∴OB⊥BC.
∵AD∥BC,
∴OB⊥AD,即OA⊥AD,
∴AD为小⊙O的切线.
(2)解:∵AD∥BC,CD∥BH,∴四边形BCDG是平行四边形.
∴DG=BC=6.
∵∠FOB=30°,BH∥FM,
∴∠OBG=30°,∠BGA=60°=∠DGH.
在Rt△DGH中,
DH=DGsin60°=6×=3.
5.证明:(1)连接OD,(1分)
∵∠BAC的平分线AD交BC于D,
∴∠OAD=∠CAD;
又∵∠OAD=∠ODA,
∴∠ODA=∠CDA,
∴OD∥AC.
∵∠ACB=90°,
∴OD⊥BC,(3分)
∴BC是⊙O的切线.∵AC=6,BC=8,
∴AB=10;
过C作CH⊥AB于H,
则CH==,(5分)
连接OC,设⊙O的半径为r;
则S△ABC=S△OBC+S△OAC=,(6分)
∴,
∴.(8分)
6.证明:(1)连接OD,
∵DE∥OC,
∴∠DEB=∠COB,∠DOC=∠ODE.
∵∠ODE=∠OED,
∴∠DOC=∠BOC.
∵OD=OD,OC=OC,
∴∠CDO=∠CBO=90°.
∴∠ODA=90°.
∴AC是⊙O的切线.
解:(2)设半径为x,则x2+4=(x+1)2
∴x=1.5
∴AB=4.
∵BC=CD,
∴CD2+16=(CD+2)2
∴CD=3.
7.(1)证明:连接OD,BD;
∵OC∥弦AD,
∴∠BOC=∠A,∠ADO=DOC.
∵OA=OD,
∴∠A=∠COD.
∴∠COD=∠BOC.
∵OC=OC,OB=OD,
∴△OCD≌△OCB.
∴∠B=∠ODC=90°.
∴CD是⊙O的切线.
(2)解:∵BC是⊙O的切线,
∴∠OBC=90°.
∵DE⊥AB,
∴∠AED=90°.
∴∠OBC=∠AED.
∵OC∥弦AD,
∴∠BOC=∠EAD.
∴△OBC∽△AED.
∴BC:DE=OB:AE.
∵PE∥BC,
∴△ABC∽△AEP.
∴BC:EP=AB:AE.
∵AB=2OB,
∴DE=2PE.
∴PD=PE.
∴PD:ED=1:2.
8.(1)证明:连接AF,则AF⊥BC;
∵AB=AC,且AF⊥BC,
∴F是BC的中点,即CF=BC=AC;
在Rt△ACF中,AC=FC,则∠FCA=45°;
即△ABC是等腰直角三角形,故AB⊥AC,
∵AB是⊙O的直径,
∴AC是⊙O的切线.
(2)解:连接AD,则AD⊥BE;
∵∠EDC=∠ODB,而∠ODB=∠OBD,
∴∠EDC=∠OBD;
由弦切角定理知:∠DAE=∠OBD,故∠EDC=∠DAE,
易得:△CDE∽△CAD,
∴,而;
即?;
由(1)知:AB=AC,故=1.
9.证明:(1)连OC.
∵AD⊥DC,
∴∠ADC=90°.
∵AC平分∠DAB,
∴∠DAC=∠CAB.
又OC=OA,
∴∠CAB=∠ACO,
∴∠DAC=∠ACO,
∴OC∥AD.
∴∠OCD=180°﹣∠ADC=90°.
又OC是⊙O的半径,
∴CD是⊙O的切线.解:连接BC;
∵AB是⊙O的直径,
∴∠ACB=90°.
又∠ADC=90°,
∴∠ADC=∠ACB=90°,
由(1)可知∠DAC=∠CAB,
∴△ACD∽△ABC.
∴而AD=2.
∴,
∴,
故AB的长为.(8分)
10.(1)证明:连接OB、OC.
∵MN是⊙O的切线,
∴OB⊥MN.
∵∠CBN=45°,
∴∠OBC=45°,∠BCE=45°.
∵OB=OC,
∴∠OBC=∠OCB=45°.
∴∠OCE=90°,
∴CE是⊙O的切线;
(2)解:∵OB⊥BE,CE⊥BE,OC⊥CE,
∴四边形BOCE是矩形,
又OB=OC,
∴四边形BOCE是正方形,
∴BE=CE=OB=OC=r.
在Rt△CDE中,
∵∠D=30°,CE=r,
∴DE=r.
∵BD=2+2,
∴r+r=2+2,
∴r=2,即⊙O的半径为2.
