人教版五年级数学下册课件4.5.2 公倍数和最小公倍数的应用 (19张PPT)
文档属性
| 名称 | 人教版五年级数学下册课件4.5.2 公倍数和最小公倍数的应用 (19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览




文档简介
5 通分
人教版数学五年级下册
4
分数的意义和性质
第2课时 公倍数和最小公倍数的应用
在小河旁住着一匹小马和一只小羊。每隔一段时间他们就会亲自到河边去打水。新年的第一天,小马和小羊相遇在小河边,再过多少天,他们可以再次在小河边相遇?
同学们,你知道这类问题如何解决吗?
3
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
二 新课探究
(教科书第70页例3)
这种墙砖长3dm,宽2dm。
你从题目中获得了哪些有效信息?
3dm
2dm
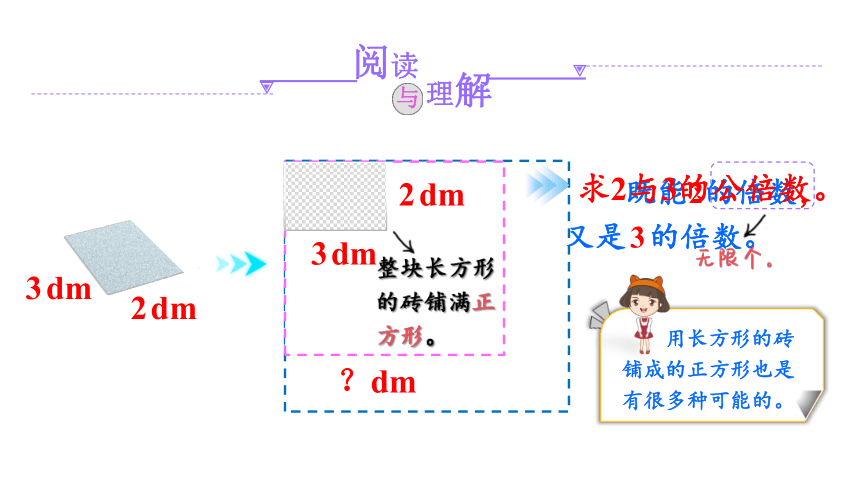
阅读
理解
与
3dm
2dm
既能2的倍数,又是3的倍数。
求2与3的公倍数。
2dm
3dm
整块长方形的砖铺满正方形。
?dm
用长方形的砖铺成的正方形也是有很多种可能的。
分析
解答
与
3的倍数:
3,6,9,12,15,18,…
2和3的的最小公倍数是6。
2×3=6
2×6=12
2和3的倍数有:6,12,18,…
2和3的公因数有6、12、18…其中最小公因数是6。所以,可以正方形边长是6dm、12dm、18dm,…,其中最小的正方形边长是6dm。
2×9=18
回顾
反思
与
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
在边长是6dm的正方形上画一画,看我找的对不对。
培优
剖析
范
例
一些小朋友分组做游戏,第一次分组每组4人余下2人,第二次分组每组5人也余下2人,第三次分组每组6人还是余下2人。问最少有多少名小朋友做游戏?
做游戏的小朋友人数减去2后,正好是4、5和6的公倍数。
培优
剖析
范
例
一些小朋友分组做游戏,第一次分组每组4人余下2人,第二次分组每组5人也余下2人,第三次分组每组6人还是余下2人。问最少有多少名小朋友做游戏?
4、5、6的最小公倍数是60。
60+2=62(名)
答:最少有62名小朋友做游戏。
判断题。
一个数的倍数的个数是无限的。
3. 2和8的最小公倍数是16。
( )
( )
2. 两个数的公倍数有无限个,最小公倍数的个
数只有1个。
( )
√
√
×
2和8的最小公倍数是8。
求出下面每组数的最小公倍数。
9和11
( )
4和10
( )
25和20
( )
12和15
( )
12和48
( )
21和84
( )
15和60
( )
13和65
( )
3和5
( )
99
20
100
60
36
84
60
65
15
9×11=99
2×2×5=20
5×5×4=100
3×4×5=60
6×2×3=36
3×7×4=84
3×5×4=60
13×5=65
3×5=15
一种长方体香水盒长6cm,宽5cm,高10cm,如果在一个正方体箱子里刚好装满了一些这种香水盒,并且没有空隙,那么箱子的棱长至少是多少厘米?
6=2×3
答:箱子的棱长至少是30厘米。
6、5、10的最小公倍数是:2×3×5=30
5=1×5
10=2×5
小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5
圈,爸爸跑了10圈,妈妈跑了8圈。
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
人教版数学五年级下册
4
分数的意义和性质
第2课时 公倍数和最小公倍数的应用
在小河旁住着一匹小马和一只小羊。每隔一段时间他们就会亲自到河边去打水。新年的第一天,小马和小羊相遇在小河边,再过多少天,他们可以再次在小河边相遇?
同学们,你知道这类问题如何解决吗?
3
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
二 新课探究
(教科书第70页例3)
这种墙砖长3dm,宽2dm。
你从题目中获得了哪些有效信息?
3dm
2dm
阅读
理解
与
3dm
2dm
既能2的倍数,又是3的倍数。
求2与3的公倍数。
2dm
3dm
整块长方形的砖铺满正方形。
?dm
用长方形的砖铺成的正方形也是有很多种可能的。
分析
解答
与
3的倍数:
3,6,9,12,15,18,…
2和3的的最小公倍数是6。
2×3=6
2×6=12
2和3的倍数有:6,12,18,…
2和3的公因数有6、12、18…其中最小公因数是6。所以,可以正方形边长是6dm、12dm、18dm,…,其中最小的正方形边长是6dm。
2×9=18
回顾
反思
与
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
在边长是6dm的正方形上画一画,看我找的对不对。
培优
剖析
范
例
一些小朋友分组做游戏,第一次分组每组4人余下2人,第二次分组每组5人也余下2人,第三次分组每组6人还是余下2人。问最少有多少名小朋友做游戏?
做游戏的小朋友人数减去2后,正好是4、5和6的公倍数。
培优
剖析
范
例
一些小朋友分组做游戏,第一次分组每组4人余下2人,第二次分组每组5人也余下2人,第三次分组每组6人还是余下2人。问最少有多少名小朋友做游戏?
4、5、6的最小公倍数是60。
60+2=62(名)
答:最少有62名小朋友做游戏。
判断题。
一个数的倍数的个数是无限的。
3. 2和8的最小公倍数是16。
( )
( )
2. 两个数的公倍数有无限个,最小公倍数的个
数只有1个。
( )
√
√
×
2和8的最小公倍数是8。
求出下面每组数的最小公倍数。
9和11
( )
4和10
( )
25和20
( )
12和15
( )
12和48
( )
21和84
( )
15和60
( )
13和65
( )
3和5
( )
99
20
100
60
36
84
60
65
15
9×11=99
2×2×5=20
5×5×4=100
3×4×5=60
6×2×3=36
3×7×4=84
3×5×4=60
13×5=65
3×5=15
一种长方体香水盒长6cm,宽5cm,高10cm,如果在一个正方体箱子里刚好装满了一些这种香水盒,并且没有空隙,那么箱子的棱长至少是多少厘米?
6=2×3
答:箱子的棱长至少是30厘米。
6、5、10的最小公倍数是:2×3×5=30
5=1×5
10=2×5
小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5
圈,爸爸跑了10圈,妈妈跑了8圈。
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
