新人教版数学七年级上 4.2直线射线线段
文档属性
| 名称 | 新人教版数学七年级上 4.2直线射线线段 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-08 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
§3.2 直线、射线、线段(1)
实验中学 高岩
学习目标
(1)能在现实情境中,经历画图的数学活动过程,理解并掌握直线的公理,能用几何语言描述直线公理.
(2)会用字母表示直线、射线、线段,会根据语言描述图形
自学 自学------质疑------解疑
认真学习教材第128-129页的内容,然后小组交流讨论,完成以下问题:
经过一点A画直线,能画出几条 过两点呢?
直线的公理:
日常生活中有哪些例子可以证明两点确定一条直线这个性质呢
怎样判断两条射线是同一射线呢?
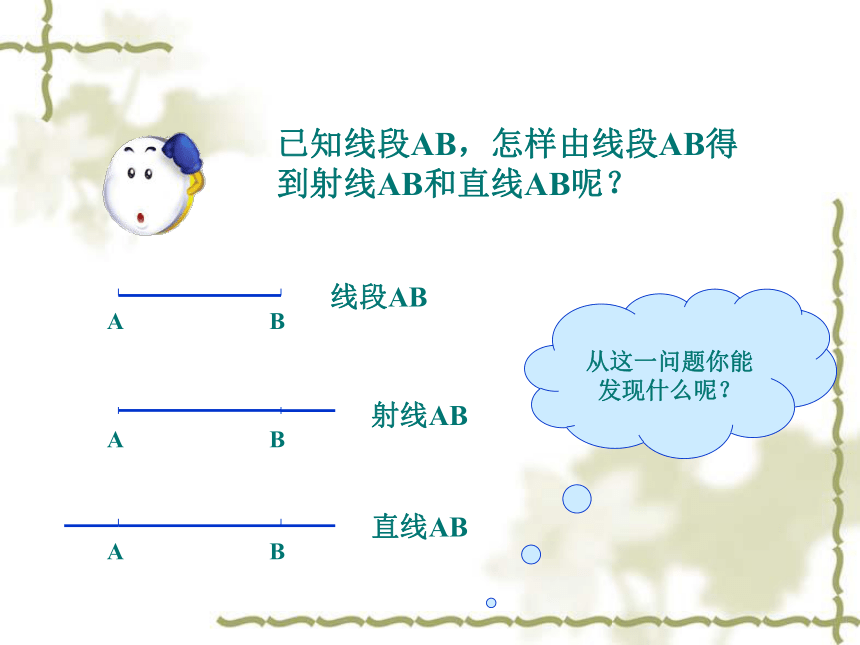
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
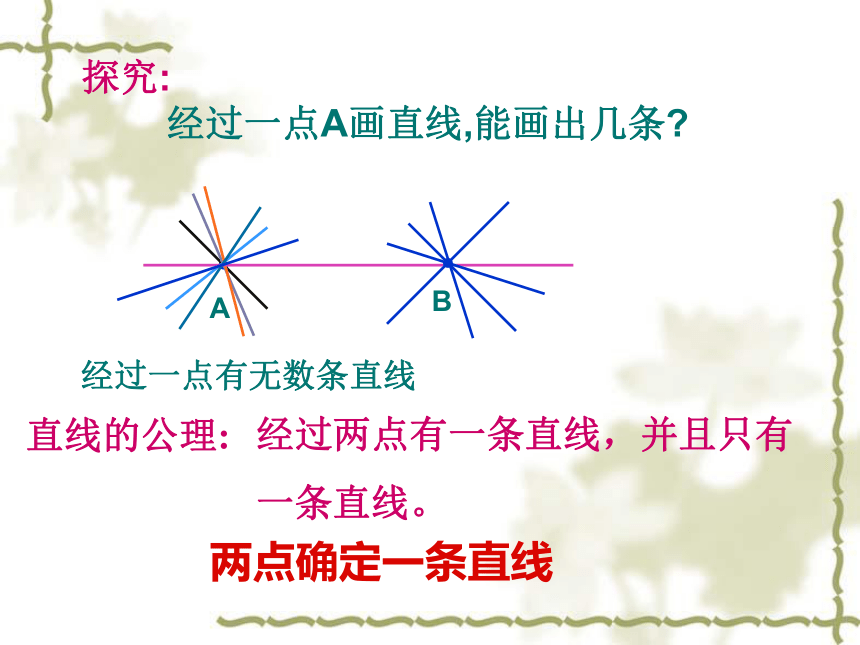
探究:
经过一点A画直线,能画出几条
经过两点有一条直线,并且只有
一条直线。
直线的公理:
两点确定一条直线
经过一点有无数条直线
A
B
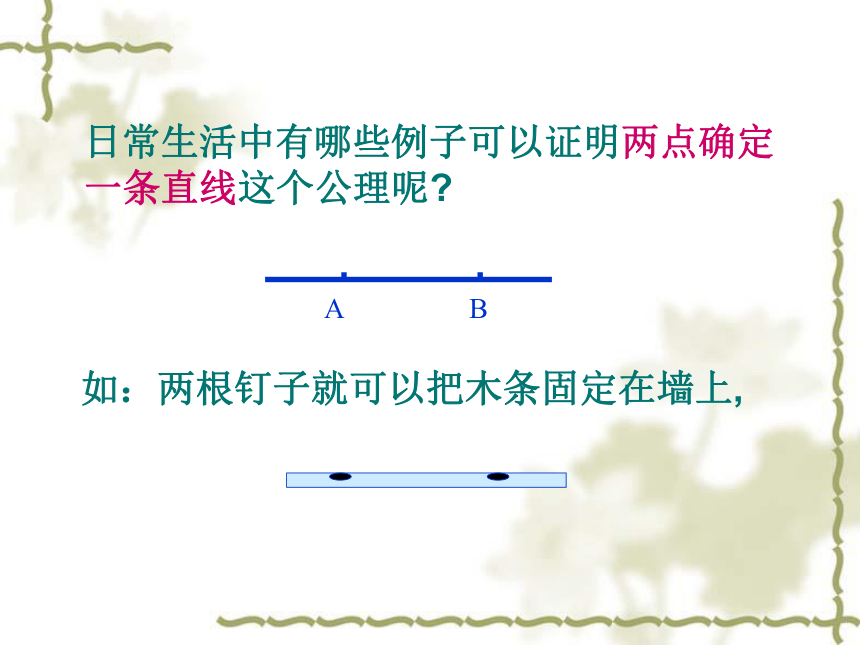
日常生活中有哪些例子可以证明两点确定一条直线这个公理呢
A
B
如:两根钉子就可以把木条固定在墙上,
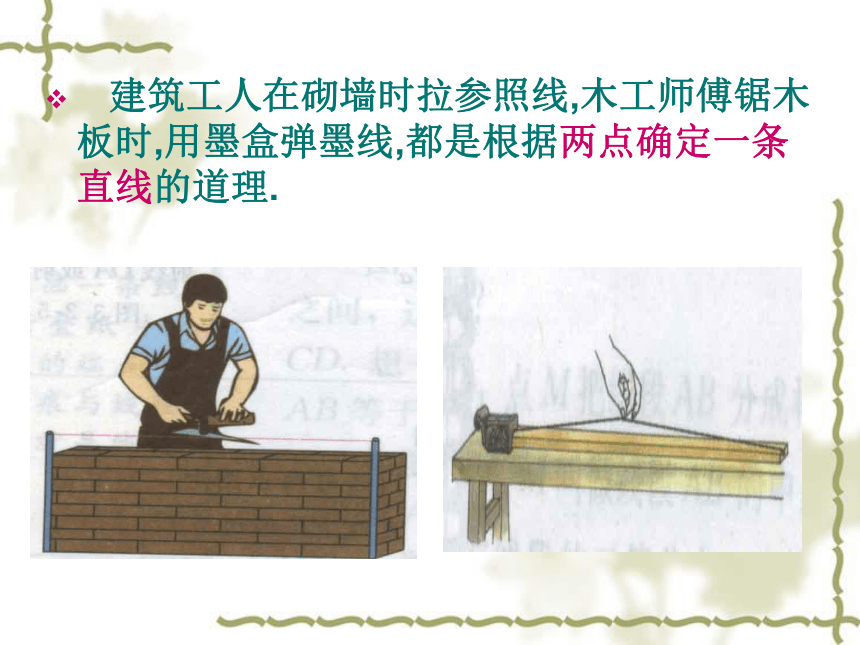
建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据两点确定一条直线的道理.
C
A
B
D
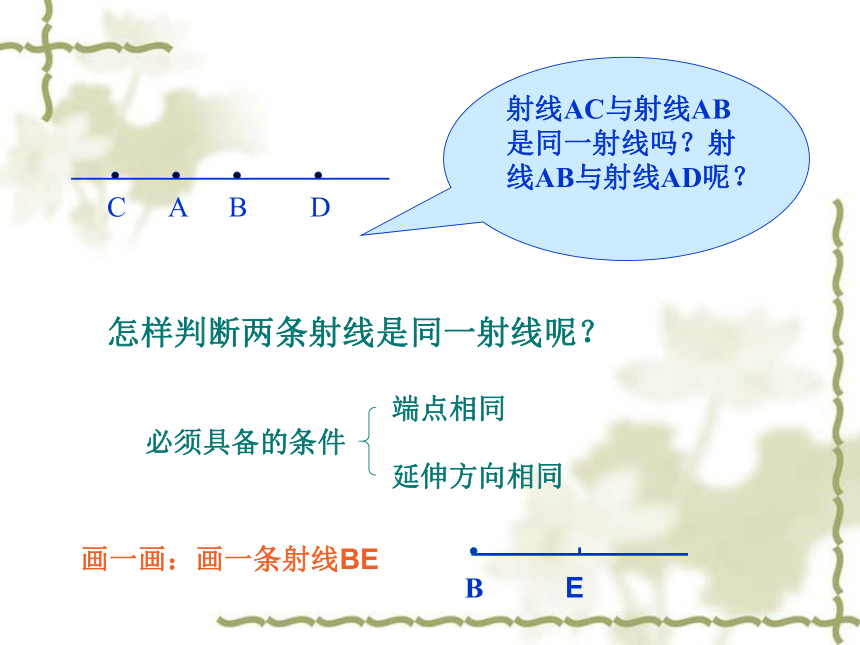
射线AC与射线AB是同一射线吗?射线AB与射线AD呢?
怎样判断两条射线是同一射线呢?
必须具备的条件
端点相同
延伸方向相同
画一画:画一条射线BE
E
B
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
A
B
线段AB
A
B
A
B
射线AB
直线AB
从这一问题你能发现什么呢?
把线段向一个方向无限延伸可得到射线,
把线段向两个方向延伸可得到直线。
线段和射线都是直线的一部分。
问题1.
(1)生活中有哪些关于“直线”的形象的例 子?试举例说明。
(2)直线的表示方法是怎样呢
数轴是规定了原点、正方向和单位长度的直线。
笔直的公路
A
B
直线AB
a
或直线 a
画一条直线CF
量学 自测------互查------互教
在我们的日常生活中有哪些有关“线段”形象的例子
线 段
A
B
线段的表示方法
线段AB
a
或线段a
线段向一个方向无限延伸就形成了
A
O
射线
射线0A
或射线 a
a
射线0A和射线AO是同一射线吗?
射线AO
O
A
图形 表示方法 端点个数 延伸方向
线段
射线
直线
直线、射线、线段的联系与区别
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸
向一方无限延伸
向两方无限延伸
A
B
a
注意:(1)表示线段、射线、直线的时候,都要在字母前注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示
射线的两个大写字母不能交换位置,必须把端点字母放在前面。
三.助学 展示------反馈------导学
.用学 自测------反馈------点拨
1.下图中,有几条直线,几条射线,几条线段?
A
B
C
D
答:有1条直线,8条射线,6条线段。
2.如图,已知三点A、B、C,
(1)画直线AB
(2)画射线AC
(3)连接BC
A
B
C
五.测学 自测------反馈------点拨
1.在墙上钉一根木条需_______个钉子,其根据是________.
2.如下图(1)所示,点A在直线L______,点B在直线L________.
3.如下图(2)所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点
4.如下图(3)所示,图中共有_____条线段,它们是________;共有______条射线,它们是________.
(2)、点A在直线a外;
(3)、经过点O的三条线段a、b、c;
(4)、线段AB、CD相交于点B。
(1)、直线EF经过点C;
E F C
A
a
a
b
c
o
A
B
C
D
5.按下列语句画出图形:
课堂小结
你对本节内容有哪些认识?
1、直线的公理:经过两点有一条直 线,并且只有一条直线。
2、掌握直线、射线、线段的表示方法
3、理解直线、射线、线段的联系和区别
§3.2 直线、射线、线段(1)
实验中学 高岩
学习目标
(1)能在现实情境中,经历画图的数学活动过程,理解并掌握直线的公理,能用几何语言描述直线公理.
(2)会用字母表示直线、射线、线段,会根据语言描述图形
自学 自学------质疑------解疑
认真学习教材第128-129页的内容,然后小组交流讨论,完成以下问题:
经过一点A画直线,能画出几条 过两点呢?
直线的公理:
日常生活中有哪些例子可以证明两点确定一条直线这个性质呢
怎样判断两条射线是同一射线呢?
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
探究:
经过一点A画直线,能画出几条
经过两点有一条直线,并且只有
一条直线。
直线的公理:
两点确定一条直线
经过一点有无数条直线
A
B
日常生活中有哪些例子可以证明两点确定一条直线这个公理呢
A
B
如:两根钉子就可以把木条固定在墙上,
建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据两点确定一条直线的道理.
C
A
B
D
射线AC与射线AB是同一射线吗?射线AB与射线AD呢?
怎样判断两条射线是同一射线呢?
必须具备的条件
端点相同
延伸方向相同
画一画:画一条射线BE
E
B
已知线段AB,怎样由线段AB得到射线AB和直线AB呢?
A
B
线段AB
A
B
A
B
射线AB
直线AB
从这一问题你能发现什么呢?
把线段向一个方向无限延伸可得到射线,
把线段向两个方向延伸可得到直线。
线段和射线都是直线的一部分。
问题1.
(1)生活中有哪些关于“直线”的形象的例 子?试举例说明。
(2)直线的表示方法是怎样呢
数轴是规定了原点、正方向和单位长度的直线。
笔直的公路
A
B
直线AB
a
或直线 a
画一条直线CF
量学 自测------互查------互教
在我们的日常生活中有哪些有关“线段”形象的例子
线 段
A
B
线段的表示方法
线段AB
a
或线段a
线段向一个方向无限延伸就形成了
A
O
射线
射线0A
或射线 a
a
射线0A和射线AO是同一射线吗?
射线AO
O
A
图形 表示方法 端点个数 延伸方向
线段
射线
直线
直线、射线、线段的联系与区别
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸
向一方无限延伸
向两方无限延伸
A
B
a
注意:(1)表示线段、射线、直线的时候,都要在字母前注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示
射线的两个大写字母不能交换位置,必须把端点字母放在前面。
三.助学 展示------反馈------导学
.用学 自测------反馈------点拨
1.下图中,有几条直线,几条射线,几条线段?
A
B
C
D
答:有1条直线,8条射线,6条线段。
2.如图,已知三点A、B、C,
(1)画直线AB
(2)画射线AC
(3)连接BC
A
B
C
五.测学 自测------反馈------点拨
1.在墙上钉一根木条需_______个钉子,其根据是________.
2.如下图(1)所示,点A在直线L______,点B在直线L________.
3.如下图(2)所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点
4.如下图(3)所示,图中共有_____条线段,它们是________;共有______条射线,它们是________.
(2)、点A在直线a外;
(3)、经过点O的三条线段a、b、c;
(4)、线段AB、CD相交于点B。
(1)、直线EF经过点C;
E F C
A
a
a
b
c
o
A
B
C
D
5.按下列语句画出图形:
课堂小结
你对本节内容有哪些认识?
1、直线的公理:经过两点有一条直 线,并且只有一条直线。
2、掌握直线、射线、线段的表示方法
3、理解直线、射线、线段的联系和区别
