31.4用列举法求简单时间的概率第二课时(树形图)-冀教版九年级数学下册课件(共20张)
文档属性
| 名称 | 31.4用列举法求简单时间的概率第二课时(树形图)-冀教版九年级数学下册课件(共20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 09:16:59 | ||
图片预览








文档简介
31.4 用列举法求简单事件的概率
第三十一章 随机事件的概率
冀教版九下
第二课时 树形图
学 习 目 标
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
创设问题情境,引入新课
问题一:掷一枚质地均匀的硬币,落地后,正面向上的概率是多少?
解:共有2种等可能的结果,其中正面向上有一种.
创设问题情境,引入新课
问题二:同时掷两枚质地均匀的硬币,落地后,两枚都是正面向上的概率是多少?
解:设正面向上为1,反面向上为2.
2
1
第一枚
第二枚
1
2
(1,1)
(1,2)
(2,1)
(2,2)
共有4种等可能的结果,其中两枚都是正面向上的有1种.
创设问题情境,引入新课
问题三:同时掷三枚质地均匀的硬币,落地后,三枚都是正面向上的概率是多少?
想一想:还能用列表法求出概率吗?
不能
今天我们学习用树形图来解决这个问题.......
新课学习
树形图的画法
开始
第一个因素
第二个因素
如一个试验中涉及2个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况.
A
B
1
2
3
1
2
3
画树形图法:按事件发生的次序,列出事件可能出现的结果.
用树形图求简单事件的概率
典例精析
例1.同时掷三枚质地均匀的硬币,落地后,求三枚都是正面向上的概率.
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
共有8种等可能的结果,其中三枚都是正面向上的有1种.
开始
总结提升
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
开始
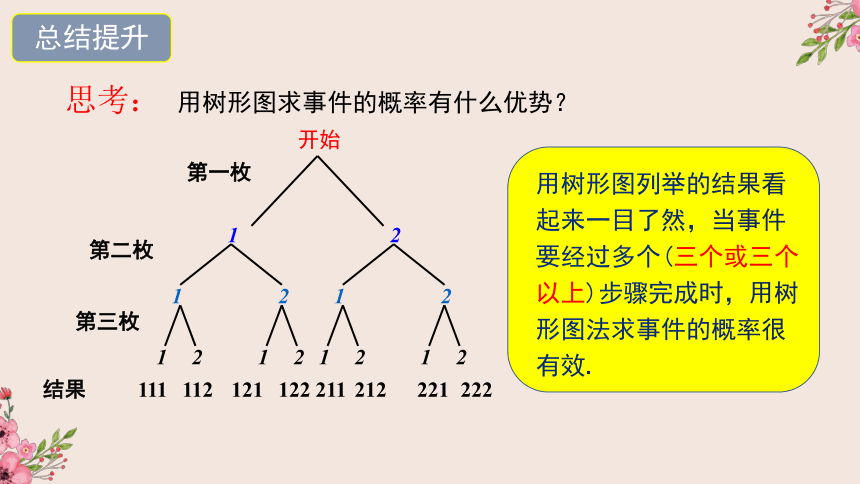
思考:
用树形图求事件的概率有什么优势?
用树形图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树形图法求事件的概率很有效.
典例精析
例2.“田忌赛马”
问题:
齐威王和田忌赛马,两人均有上、中、下三种马.同一级别的马,齐王的马要优于田忌的马,但是田忌的上等马优于齐王的中等马,中等马优于齐王的下等马.
假如齐王的马出阵的顺序是上、中、下,田忌的马随意出阵,田忌赢的概率是多大?
想一想:
孙膑给田忌献策,使田忌赢得了比赛,孙膑的计策是什么呢?
新课学习
开始
上
中
下
中
下
上
上
下
中
下
上
中
中
下
上
第一场
第二场
第三场
结果
上 中 下
上 下 中
中 上 下
中 下 上
下 上 中
下 中 上
共有6种等可能的结果,其中田忌赢的有1种.
总结提升
例1和例2的相同点和不同点分别是什么?
思考:
相同点:
事件要经过3个步骤完成,需要画三层树形图.
不同点:
例1属于“有放回”.
例2属于“不放回”.
注意:在用树形图求一个事件的概率时,仍然要先关注属于“有放回”还是“不放回”.
巩固练习
1.学校要选一个同学去参加市里的数学竞赛,在全校的数学选拔赛中,有甲、乙、丙三位同学均获得了满分.老师决定用抽签的方式从甲、乙、丙中选择一人参加竞赛.
取3张大小相同,分别标有数字1,2,3的3张的卡片,充分混匀后扣到桌子上,按甲、乙、丙的顺序,每人从中任意抽取一张,规定抽到1号卡片的人去市里参加竞赛。这样做公平吗?
巩固练习
分析:
当甲、乙、丙取得1号卡片的概率相同时,是公平的,否则,不公平.
开始
1
2
3
1
2
3
3
1
2
3
1
2
2
3
1
甲
乙
丙
结果
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
共有6种等可能的结果,其中甲、乙、丙取得1号卡片都是2种.
甲
甲
乙
丙
乙
丙
典例精析
例3.袋子中3个红球,2个黄球.甲先从中任取1个球,取后不放回,乙再从中取1个球.求两人取到的是一个红球和一个黄球的概率.
用列表法和树形图,哪一种更合适一些?
试一试:
同桌俩,一人用列表法,一人用树形图。然后作比较.
由于同一层中,可能情况较多,画树形图时树叉较多,图形看起来乱,此时用列表法较整齐,比较合适.
典例精析
方法二:
开始
设红球为A,黄球为B.
A
B
A
A
B
B
甲
乙
结果
AA
AB
BA
BB
对应概率
巩固练习
1.现有四个外观完全一样的粽子,其中有且只有一个有蛋黄,若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( ).
分析:
设有蛋黄为A,
没有蛋黄为B.
开始
A
B
A
B
B
第一个
第二个
结果
AB
BA
BB
对应概率
巩固练习
1.现有四个外观完全一样的粽子,其中有且只有一个有蛋黄,若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( ).
分析:
分析总结
两种树形图的不同之处.
第一种:同一层,从每个节点等可能地分出数目相同的分支;
总结:
第二种:同一层,从节点分成的分支不是等可能的.
课堂小结
1.列表法(两层,且每层的数目较多)
求一个简单事件的概率时
2.树形图(两层及以上都可用)
3.直接列举法(结果较多时)
根据实际问题,选择合适的方法去求事件的概率.
同学们再见
第三十一章 随机事件的概率
冀教版九下
第二课时 树形图
学 习 目 标
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
创设问题情境,引入新课
问题一:掷一枚质地均匀的硬币,落地后,正面向上的概率是多少?
解:共有2种等可能的结果,其中正面向上有一种.
创设问题情境,引入新课
问题二:同时掷两枚质地均匀的硬币,落地后,两枚都是正面向上的概率是多少?
解:设正面向上为1,反面向上为2.
2
1
第一枚
第二枚
1
2
(1,1)
(1,2)
(2,1)
(2,2)
共有4种等可能的结果,其中两枚都是正面向上的有1种.
创设问题情境,引入新课
问题三:同时掷三枚质地均匀的硬币,落地后,三枚都是正面向上的概率是多少?
想一想:还能用列表法求出概率吗?
不能
今天我们学习用树形图来解决这个问题.......
新课学习
树形图的画法
开始
第一个因素
第二个因素
如一个试验中涉及2个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况.
A
B
1
2
3
1
2
3
画树形图法:按事件发生的次序,列出事件可能出现的结果.
用树形图求简单事件的概率
典例精析
例1.同时掷三枚质地均匀的硬币,落地后,求三枚都是正面向上的概率.
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
共有8种等可能的结果,其中三枚都是正面向上的有1种.
开始
总结提升
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
开始
思考:
用树形图求事件的概率有什么优势?
用树形图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树形图法求事件的概率很有效.
典例精析
例2.“田忌赛马”
问题:
齐威王和田忌赛马,两人均有上、中、下三种马.同一级别的马,齐王的马要优于田忌的马,但是田忌的上等马优于齐王的中等马,中等马优于齐王的下等马.
假如齐王的马出阵的顺序是上、中、下,田忌的马随意出阵,田忌赢的概率是多大?
想一想:
孙膑给田忌献策,使田忌赢得了比赛,孙膑的计策是什么呢?
新课学习
开始
上
中
下
中
下
上
上
下
中
下
上
中
中
下
上
第一场
第二场
第三场
结果
上 中 下
上 下 中
中 上 下
中 下 上
下 上 中
下 中 上
共有6种等可能的结果,其中田忌赢的有1种.
总结提升
例1和例2的相同点和不同点分别是什么?
思考:
相同点:
事件要经过3个步骤完成,需要画三层树形图.
不同点:
例1属于“有放回”.
例2属于“不放回”.
注意:在用树形图求一个事件的概率时,仍然要先关注属于“有放回”还是“不放回”.
巩固练习
1.学校要选一个同学去参加市里的数学竞赛,在全校的数学选拔赛中,有甲、乙、丙三位同学均获得了满分.老师决定用抽签的方式从甲、乙、丙中选择一人参加竞赛.
取3张大小相同,分别标有数字1,2,3的3张的卡片,充分混匀后扣到桌子上,按甲、乙、丙的顺序,每人从中任意抽取一张,规定抽到1号卡片的人去市里参加竞赛。这样做公平吗?
巩固练习
分析:
当甲、乙、丙取得1号卡片的概率相同时,是公平的,否则,不公平.
开始
1
2
3
1
2
3
3
1
2
3
1
2
2
3
1
甲
乙
丙
结果
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
共有6种等可能的结果,其中甲、乙、丙取得1号卡片都是2种.
甲
甲
乙
丙
乙
丙
典例精析
例3.袋子中3个红球,2个黄球.甲先从中任取1个球,取后不放回,乙再从中取1个球.求两人取到的是一个红球和一个黄球的概率.
用列表法和树形图,哪一种更合适一些?
试一试:
同桌俩,一人用列表法,一人用树形图。然后作比较.
由于同一层中,可能情况较多,画树形图时树叉较多,图形看起来乱,此时用列表法较整齐,比较合适.
典例精析
方法二:
开始
设红球为A,黄球为B.
A
B
A
A
B
B
甲
乙
结果
AA
AB
BA
BB
对应概率
巩固练习
1.现有四个外观完全一样的粽子,其中有且只有一个有蛋黄,若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( ).
分析:
设有蛋黄为A,
没有蛋黄为B.
开始
A
B
A
B
B
第一个
第二个
结果
AB
BA
BB
对应概率
巩固练习
1.现有四个外观完全一样的粽子,其中有且只有一个有蛋黄,若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( ).
分析:
分析总结
两种树形图的不同之处.
第一种:同一层,从每个节点等可能地分出数目相同的分支;
总结:
第二种:同一层,从节点分成的分支不是等可能的.
课堂小结
1.列表法(两层,且每层的数目较多)
求一个简单事件的概率时
2.树形图(两层及以上都可用)
3.直接列举法(结果较多时)
根据实际问题,选择合适的方法去求事件的概率.
同学们再见
