31.4用列举法求简单时间的概率第一课时(列表法)-冀教版九年级数学下册课件(21张)
文档属性
| 名称 | 31.4用列举法求简单时间的概率第一课时(列表法)-冀教版九年级数学下册课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览






文档简介
31.4 用列举法求简单事件的概率
第三十一章 随机事件的概率
冀教版九下
第一课时 列表法
学 习 目 标
1.会利用“列表法”求随机事件的概率.
2.会区分问题中的“有放回”和“不放回”.
创设问题情境,引入新课
情境:在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.
(1)从中任意摸出一个球是红球的概率是多少?
解:共有3种等可能的结果,其中摸到红球有两种.
2个红球
1个白球
(2)若从中任意摸出两个球都是红球的概率是多少呢?
创设问题情境,引入新课
你是怎么解决这个问题的.
谈一谈:
今天我们就来学习用列表法求一个简单事件的概率的方法......
学生说出自己的方法和观点
新课学习
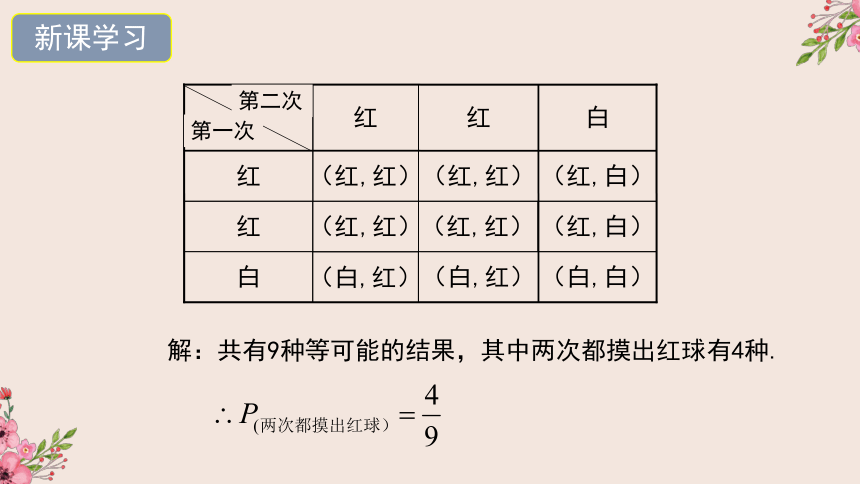
例1.在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.从中任意摸出一个球后,放回搅匀后再摸出一个球,求两次摸出的球都是红球的概率.
分析: 当一次试验要涉及两个因素,为不重不漏地列出所有可能结果,通常采用列表法.
新课学习
白
红
(红,白)
(白,白)
(白,红)
(白,红)
(红,红)
(红,红)
(红,白)
(红,红)
(红,红)
红
白
红
红
第一次
第二次
解:共有9种等可能的结果,其中两次都摸出红球有4种.
新课学习
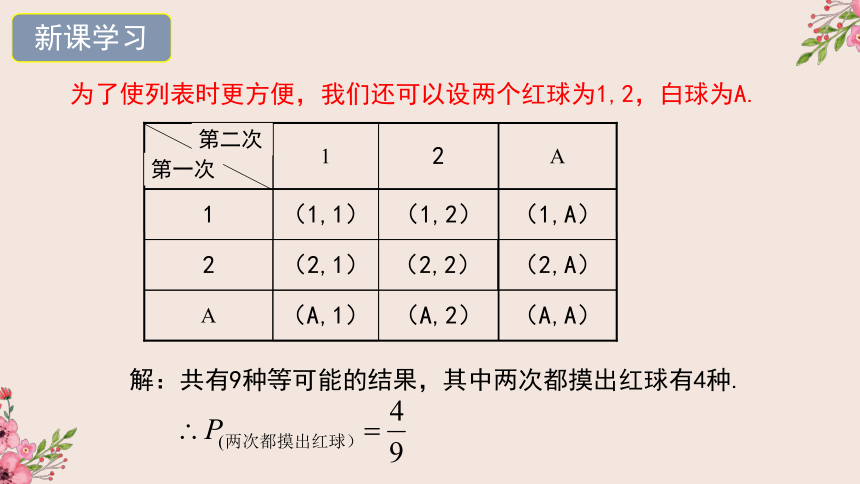
A
2
(2,A)
(A,A)
(A,2)
(A,1)
(2,2)
(2,1)
(1,A)
(1,2)
(1,1)
1
A
2
1
第一次
第二次
解:共有9种等可能的结果,其中两次都摸出红球有4种.
为了使列表时更方便,我们还可以设两个红球为1,2,白球为A.
新课学习
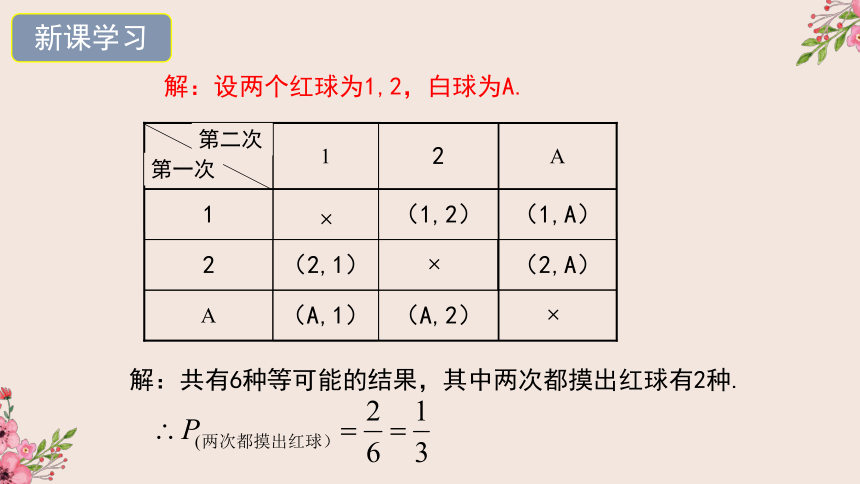
例1.(变式)在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.从中任意摸出一个球后,不放回再摸出一个球,求两次摸出的球都是红球的概率.
注意:
这个问题与上一问题的不同之处是什么?
摸出第一个球后不再放回.
想一想:
列表时要注意什么?
新课学习
A
2
(2,A)
(A,2)
(A,1)
(2,1)
(1,A)
(1,2)
1
A
2
1
第一次
第二次
解:共有6种等可能的结果,其中两次都摸出红球有2种.
解:设两个红球为1,2,白球为A.
×
×
×
新课学习
从例1中给出的两个问题,你有什么思考和总结?
思考:
两个问题中,同是求摸到两个红球的概率,但由于第二次摸球时,有“放回”和“不放回”的区别,从而求得的概率不同.因此求概率时,要关注问题中是属于“放回”还是“不放回”.
巩固练习
1.小明有一双黑袜子和一双白袜子,早上小明随手拿起两只袜子穿到脚上,求小明穿的是同一颜色袜子的概率.
1
2
A
B
1
2
A
B
第二只
第一只
(1,2)
(1,A)
(1,B)
(2,1)
(2,A)
(2,B)
(A,1)
(A,2)
(A,B)
(B,1)
(B,2)
(B,A)
解:设黑袜子是1,2,白袜子是A,B.
×
×
×
×
共有12种等可能的结果,其中穿同一颜色袜子的有4种.
“不放回”
巩固练习
2.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( ).
3.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
新课学习
例2.四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置.当连续按对两个按钮点亮两盏灯时,“闯关成功”;而只要按错一个按钮,就会发出“闯关失败”的声音.求“闯关成功”的概率.
你能用列表法解决这个问题吗?
试一试:
1
2
3
4
新课学习
1
2
3
4
1
2
3
4
第二个
第一个
(1,2)
(1,3)
(1,4)
(2,1)
(2,3)
(2,4)
(3,1)
(3,2)
(3,4)
(4,1)
(4,2)
(4,3)
×
×
×
×
解:设1号,2号按钮各控制一盏灯.
共有12种等可能的结果,其中“闯关成功”有2种.
方法一:
新课学习
不考虑按钮的顺序,把所有的可能结果列举如下:
12 13 14 23 24 34
方法二:
共有6种等可能的结果,其中“闯关成功”有1种.
直接列举法
分析总结
方法一与方法二的不同之处.
方法一:列表法.考虑按钮的顺序,即(1,2)和(2,1)属于不同的结果.
总结:
方法二:直接列表法.不考虑按钮的顺序,即(1,2)和(2,1)属于同一种结果.
巩固练习
从长分别为1,2,3,4,5,6的六条线段中任意选择三条,事件A表示“这三条线段能构成三角形”.计算事件A的概率.
分析:
问题中有三个因素,显然不能用列表法解决,因此选择直接列举法.
巩固练习
从长分别为1,2,3,4,5,6的六条线段中任意选择三条,事件A表示“这三条线段能构成三角形”.计算事件A的概率.
解:列举出所有可能的结果如下:
123 124 125 126 134 135 136
145 146 156 234 235 236 245
246 256 345 346 356 456
共有20种等可能的结果,其中事件A有7种.
课堂小结
列表法求概率应注意的问题
确保试验中每种结果出现的可能性大小相等.
第一步:列表格;
第二步:在所有可能情况n中,再找到满足条件的事件的个数k;
第三步:代入概率公式 计算事件的概率.
列表法求概率的基本步骤
课堂小结
在求概率时,要注意:
1.“放回”和“不放回”
2.“按顺序”和“不按顺序”
同学们再见
第三十一章 随机事件的概率
冀教版九下
第一课时 列表法
学 习 目 标
1.会利用“列表法”求随机事件的概率.
2.会区分问题中的“有放回”和“不放回”.
创设问题情境,引入新课
情境:在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.
(1)从中任意摸出一个球是红球的概率是多少?
解:共有3种等可能的结果,其中摸到红球有两种.
2个红球
1个白球
(2)若从中任意摸出两个球都是红球的概率是多少呢?
创设问题情境,引入新课
你是怎么解决这个问题的.
谈一谈:
今天我们就来学习用列表法求一个简单事件的概率的方法......
学生说出自己的方法和观点
新课学习
例1.在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.从中任意摸出一个球后,放回搅匀后再摸出一个球,求两次摸出的球都是红球的概率.
分析: 当一次试验要涉及两个因素,为不重不漏地列出所有可能结果,通常采用列表法.
新课学习
白
红
(红,白)
(白,白)
(白,红)
(白,红)
(红,红)
(红,红)
(红,白)
(红,红)
(红,红)
红
白
红
红
第一次
第二次
解:共有9种等可能的结果,其中两次都摸出红球有4种.
新课学习
A
2
(2,A)
(A,A)
(A,2)
(A,1)
(2,2)
(2,1)
(1,A)
(1,2)
(1,1)
1
A
2
1
第一次
第二次
解:共有9种等可能的结果,其中两次都摸出红球有4种.
为了使列表时更方便,我们还可以设两个红球为1,2,白球为A.
新课学习
例1.(变式)在不透明的箱子里有大小、质地完全相同的3个球,其中2个是红球,1个是白球.从中任意摸出一个球后,不放回再摸出一个球,求两次摸出的球都是红球的概率.
注意:
这个问题与上一问题的不同之处是什么?
摸出第一个球后不再放回.
想一想:
列表时要注意什么?
新课学习
A
2
(2,A)
(A,2)
(A,1)
(2,1)
(1,A)
(1,2)
1
A
2
1
第一次
第二次
解:共有6种等可能的结果,其中两次都摸出红球有2种.
解:设两个红球为1,2,白球为A.
×
×
×
新课学习
从例1中给出的两个问题,你有什么思考和总结?
思考:
两个问题中,同是求摸到两个红球的概率,但由于第二次摸球时,有“放回”和“不放回”的区别,从而求得的概率不同.因此求概率时,要关注问题中是属于“放回”还是“不放回”.
巩固练习
1.小明有一双黑袜子和一双白袜子,早上小明随手拿起两只袜子穿到脚上,求小明穿的是同一颜色袜子的概率.
1
2
A
B
1
2
A
B
第二只
第一只
(1,2)
(1,A)
(1,B)
(2,1)
(2,A)
(2,B)
(A,1)
(A,2)
(A,B)
(B,1)
(B,2)
(B,A)
解:设黑袜子是1,2,白袜子是A,B.
×
×
×
×
共有12种等可能的结果,其中穿同一颜色袜子的有4种.
“不放回”
巩固练习
2.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( ).
3.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
新课学习
例2.四个开关按钮中有两个各控制一盏灯,另两个按钮控制一个发音装置.当连续按对两个按钮点亮两盏灯时,“闯关成功”;而只要按错一个按钮,就会发出“闯关失败”的声音.求“闯关成功”的概率.
你能用列表法解决这个问题吗?
试一试:
1
2
3
4
新课学习
1
2
3
4
1
2
3
4
第二个
第一个
(1,2)
(1,3)
(1,4)
(2,1)
(2,3)
(2,4)
(3,1)
(3,2)
(3,4)
(4,1)
(4,2)
(4,3)
×
×
×
×
解:设1号,2号按钮各控制一盏灯.
共有12种等可能的结果,其中“闯关成功”有2种.
方法一:
新课学习
不考虑按钮的顺序,把所有的可能结果列举如下:
12 13 14 23 24 34
方法二:
共有6种等可能的结果,其中“闯关成功”有1种.
直接列举法
分析总结
方法一与方法二的不同之处.
方法一:列表法.考虑按钮的顺序,即(1,2)和(2,1)属于不同的结果.
总结:
方法二:直接列表法.不考虑按钮的顺序,即(1,2)和(2,1)属于同一种结果.
巩固练习
从长分别为1,2,3,4,5,6的六条线段中任意选择三条,事件A表示“这三条线段能构成三角形”.计算事件A的概率.
分析:
问题中有三个因素,显然不能用列表法解决,因此选择直接列举法.
巩固练习
从长分别为1,2,3,4,5,6的六条线段中任意选择三条,事件A表示“这三条线段能构成三角形”.计算事件A的概率.
解:列举出所有可能的结果如下:
123 124 125 126 134 135 136
145 146 156 234 235 236 245
246 256 345 346 356 456
共有20种等可能的结果,其中事件A有7种.
课堂小结
列表法求概率应注意的问题
确保试验中每种结果出现的可能性大小相等.
第一步:列表格;
第二步:在所有可能情况n中,再找到满足条件的事件的个数k;
第三步:代入概率公式 计算事件的概率.
列表法求概率的基本步骤
课堂小结
在求概率时,要注意:
1.“放回”和“不放回”
2.“按顺序”和“不按顺序”
同学们再见
