32.1投影 冀教版数学九下课件(共25张)
文档属性
| 名称 | 32.1投影 冀教版数学九下课件(共25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览







文档简介
32.1 投影
第三十二章 投影与试图
冀教版九下
学 习 目 标
1.了解投影和中心投影的含义,知道平行投影和正投影的含义;
2.通过观察、想象,能根据灯光来辨别物体的影子,初步进行中心投影条件下物体与其投影之间的相互转化;
3.会利用平行投影的性质进行相关计算.
冀教版九下
创设情境,引入新课
情境一:物体在灯光下下会形成影子.
这种现象就是投影,光线是投影线,墙面、地面是投影面.
创设情境,引入新课
情境二:物体在太阳光下会形成影子.
物体在光线的照射下会形成影子,这些影子有什么特征呢?
新课学习
1.概念:蜡烛和灯泡的光线可以看做是从一个点射出的。由
一点射出的光线照射在物体上所形成的投影,叫做中心投影.
一、中心投影
2.特点:
中心投影中,物体的投影的大小与其距光源的远近_____.
在教室的灯光下,将手掌平放,手掌距灯越近,影子就越_____.
在路灯下行走,距路灯越近影子就越_____.
有关
如:
大
小
课堂小练
如图,一个广场中央有一盏路灯.
不一定一样长,只有在距离路灯的距离相等时候影子才会一样长.
(1)高矮相同的两个人在这盏路灯下的影子一定一样长吗?如果不一定,那么什么情况下他们的影子一样长?
课堂小练
(2)高矮不同的两个人在这盏路灯下的影子有可能一样长吗?
有可能,此时个子高的离路灯近,个子矮的离路灯远.
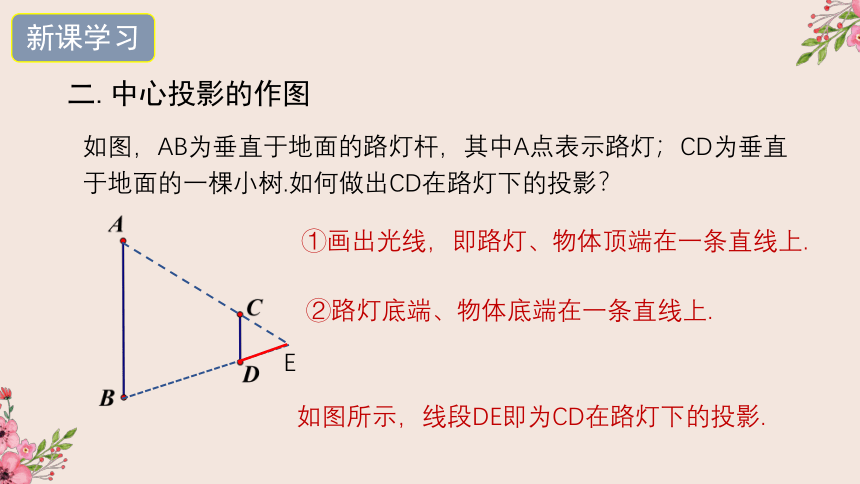
二.中心投影的作图
如图,AB为垂直于地面的路灯杆,其中A点表示路灯;CD为垂直于地面的一棵小树.如何做出CD在路灯下的投影?
新课学习
E
①画出光线,即路灯、物体顶端在一条直线上.
②路灯底端、物体底端在一条直线上.
如图所示,线段DE即为CD在路灯下的投影.
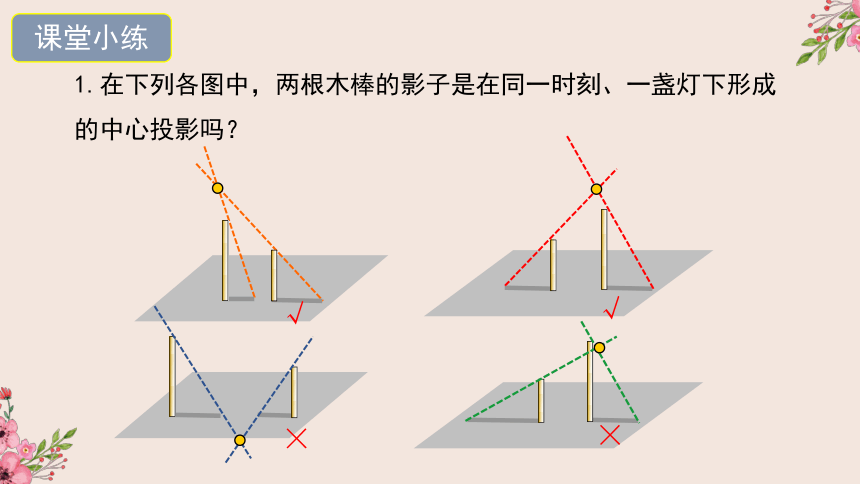
课堂小练
1.在下列各图中,两根木棒的影子是在同一时刻、一盏灯下形成的中心投影吗?
√
√
×
×
新课学习
三.平行投影
1.概念:太阳光线和探照灯的光线可以看做是平行的.像这样,
由平行光线照射在物体上所形成的投影,叫做平行投影.
2.特点:
平行投影中,物体的投影形状、大小与其摆放位置____.
有关
相同时刻,直立于地面的物体的高度与其投影_____.
成正比
课堂小练
下图中三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄.
(1)在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.
(甲)
(乙)
(丙)
→ → .
( 丙 )
( 甲 )
( 乙 )
课堂小练
(2)观察在平行投影中,直立于地面的两棵树的影子有什么关系?
影子平行
①光线平行
(3)观察在平行投影中,具有平行关系的有哪些?
②物体平行时,影子平行
新课学习
四.平行投影的作图
如图,AB为垂直于地面的旗杆,BE是旗杆AB在阳光下的影子;CD是垂直于地面的一棵小树.如何做出CD在阳光下的投影?
F
连接AE,则AE为此时是太阳光线
过点C作AE的平行线
过点D作BE的平行线
两平行线交于点F.
DF即为CD在阳光下的投影
“光线平行”
“影子平行”
课堂小练
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
(甲)
(乙)
A
D
D?
B
E
E?
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D?
B
E
E?
课堂小练
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?
解:因为△ADD ?∽△BEE?,所以,
所以,甲木杆的高度为1.86m.
(甲)
(乙)
A
D
D?
B
E
E?
课堂小练
新课学习
五.正投影
1.概念:我们把投影线垂直照射在投影面上的物体的投影叫做
正投影.
关键点:
投影线于投影面垂直
是后面学习“视图”的基础
观察与思考
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(1)四边形A'B'C'D'是什么四边形?正方体R面的对面的正投影是什么图形?
四边形A'B'C'D'是正方形
R面的对面的正投影是正方形,即四边形A'B'C'D'
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(2)正方体Q面和P面的正投影分别是什么图形?
Q面的正投影是线段B'C'
Q
P
P面的正投影是线段A'B'
观察与思考
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(3)棱AB和棱AE的正投影分别是什么图形?正方体的顶点A和顶点E的正投影分别是什么图形?
棱AB的正投影是线段A'B'
棱AE的正投影是点A'
顶点A和顶点E的正投影都是点A'
观察与思考
典例精析
例题:一位同学想利用树影测树高,已知在某一时刻直立于地面的长1.5m的竹竿的影长为3m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高CD=1.2m,地面部分影长BD=5.4m,求树高AB.
A
B
D
C
E
解:过点D作DE∥AC交AB于点E.
∵四边形AEDC为平行四边形,
∴AE=CD=1.2m.
∴AB=AE+EB=3.9m.
∴树高AB为3.9m.
方法一:
典例精析
A
B
D
C
解:延长AC交BD的延长线于点E.
∴BE=BD+DE=7.8 m.
∴树高AB为3.9m.
E
方法二:
通过添加辅助线转化为基本图形
课堂小结
投影
投影的概念
中心投影
物体在光线的照射下,会在地面或其
他平面上留下它的影子,这就是投影.
概念:点光源的光线形成的投影.
变化规律:垂直于地面的物体离点光源距离
近时,影子短,离光源远时影子长.
作图
光源与物体顶端在一条直线上.
光源与地面的垂直点与物体底端在一直线上.
课堂小结
平行投影与
正投影
概念:平行光线所形成的投影
平行光线与投影面垂直时形成的投影
平行投影
正投影
画法
计算
同学们再见
第三十二章 投影与试图
冀教版九下
学 习 目 标
1.了解投影和中心投影的含义,知道平行投影和正投影的含义;
2.通过观察、想象,能根据灯光来辨别物体的影子,初步进行中心投影条件下物体与其投影之间的相互转化;
3.会利用平行投影的性质进行相关计算.
冀教版九下
创设情境,引入新课
情境一:物体在灯光下下会形成影子.
这种现象就是投影,光线是投影线,墙面、地面是投影面.
创设情境,引入新课
情境二:物体在太阳光下会形成影子.
物体在光线的照射下会形成影子,这些影子有什么特征呢?
新课学习
1.概念:蜡烛和灯泡的光线可以看做是从一个点射出的。由
一点射出的光线照射在物体上所形成的投影,叫做中心投影.
一、中心投影
2.特点:
中心投影中,物体的投影的大小与其距光源的远近_____.
在教室的灯光下,将手掌平放,手掌距灯越近,影子就越_____.
在路灯下行走,距路灯越近影子就越_____.
有关
如:
大
小
课堂小练
如图,一个广场中央有一盏路灯.
不一定一样长,只有在距离路灯的距离相等时候影子才会一样长.
(1)高矮相同的两个人在这盏路灯下的影子一定一样长吗?如果不一定,那么什么情况下他们的影子一样长?
课堂小练
(2)高矮不同的两个人在这盏路灯下的影子有可能一样长吗?
有可能,此时个子高的离路灯近,个子矮的离路灯远.
二.中心投影的作图
如图,AB为垂直于地面的路灯杆,其中A点表示路灯;CD为垂直于地面的一棵小树.如何做出CD在路灯下的投影?
新课学习
E
①画出光线,即路灯、物体顶端在一条直线上.
②路灯底端、物体底端在一条直线上.
如图所示,线段DE即为CD在路灯下的投影.
课堂小练
1.在下列各图中,两根木棒的影子是在同一时刻、一盏灯下形成的中心投影吗?
√
√
×
×
新课学习
三.平行投影
1.概念:太阳光线和探照灯的光线可以看做是平行的.像这样,
由平行光线照射在物体上所形成的投影,叫做平行投影.
2.特点:
平行投影中,物体的投影形状、大小与其摆放位置____.
有关
相同时刻,直立于地面的物体的高度与其投影_____.
成正比
课堂小练
下图中三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄.
(1)在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.
(甲)
(乙)
(丙)
→ → .
( 丙 )
( 甲 )
( 乙 )
课堂小练
(2)观察在平行投影中,直立于地面的两棵树的影子有什么关系?
影子平行
①光线平行
(3)观察在平行投影中,具有平行关系的有哪些?
②物体平行时,影子平行
新课学习
四.平行投影的作图
如图,AB为垂直于地面的旗杆,BE是旗杆AB在阳光下的影子;CD是垂直于地面的一棵小树.如何做出CD在阳光下的投影?
F
连接AE,则AE为此时是太阳光线
过点C作AE的平行线
过点D作BE的平行线
两平行线交于点F.
DF即为CD在阳光下的投影
“光线平行”
“影子平行”
课堂小练
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
(甲)
(乙)
A
D
D?
B
E
E?
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D?
B
E
E?
课堂小练
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?
解:因为△ADD ?∽△BEE?,所以,
所以,甲木杆的高度为1.86m.
(甲)
(乙)
A
D
D?
B
E
E?
课堂小练
新课学习
五.正投影
1.概念:我们把投影线垂直照射在投影面上的物体的投影叫做
正投影.
关键点:
投影线于投影面垂直
是后面学习“视图”的基础
观察与思考
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(1)四边形A'B'C'D'是什么四边形?正方体R面的对面的正投影是什么图形?
四边形A'B'C'D'是正方形
R面的对面的正投影是正方形,即四边形A'B'C'D'
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(2)正方体Q面和P面的正投影分别是什么图形?
Q面的正投影是线段B'C'
Q
P
P面的正投影是线段A'B'
观察与思考
如图,正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.
R
(3)棱AB和棱AE的正投影分别是什么图形?正方体的顶点A和顶点E的正投影分别是什么图形?
棱AB的正投影是线段A'B'
棱AE的正投影是点A'
顶点A和顶点E的正投影都是点A'
观察与思考
典例精析
例题:一位同学想利用树影测树高,已知在某一时刻直立于地面的长1.5m的竹竿的影长为3m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高CD=1.2m,地面部分影长BD=5.4m,求树高AB.
A
B
D
C
E
解:过点D作DE∥AC交AB于点E.
∵四边形AEDC为平行四边形,
∴AE=CD=1.2m.
∴AB=AE+EB=3.9m.
∴树高AB为3.9m.
方法一:
典例精析
A
B
D
C
解:延长AC交BD的延长线于点E.
∴BE=BD+DE=7.8 m.
∴树高AB为3.9m.
E
方法二:
通过添加辅助线转化为基本图形
课堂小结
投影
投影的概念
中心投影
物体在光线的照射下,会在地面或其
他平面上留下它的影子,这就是投影.
概念:点光源的光线形成的投影.
变化规律:垂直于地面的物体离点光源距离
近时,影子短,离光源远时影子长.
作图
光源与物体顶端在一条直线上.
光源与地面的垂直点与物体底端在一直线上.
课堂小结
平行投影与
正投影
概念:平行光线所形成的投影
平行光线与投影面垂直时形成的投影
平行投影
正投影
画法
计算
同学们再见
