北师大版 九年级数学下册 3.4圆周角和圆心角的关系课件(共20张)
文档属性
| 名称 | 北师大版 九年级数学下册 3.4圆周角和圆心角的关系课件(共20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 791.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 09:21:12 | ||
图片预览



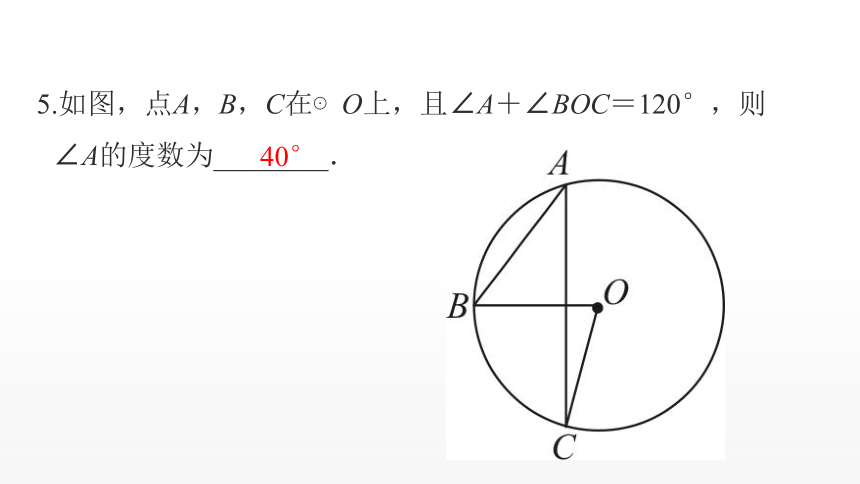
文档简介
第5课 圆周角和圆心角的关系(1)
一、新课学习
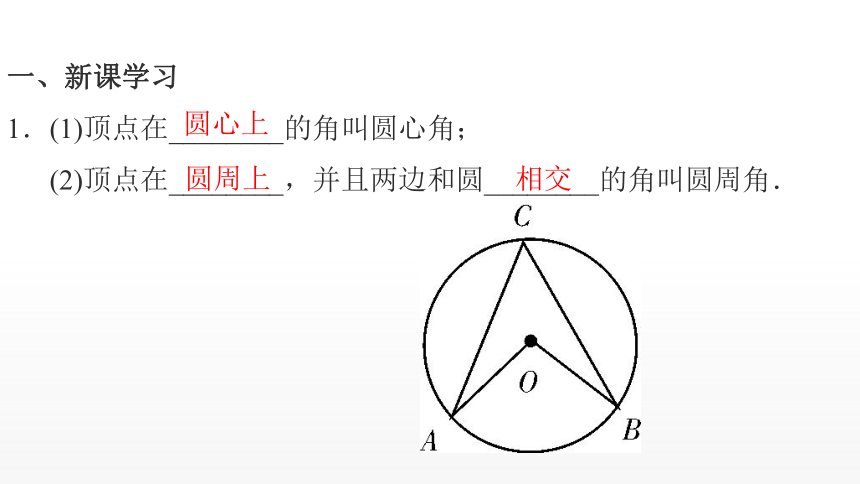
1.(1)顶点在________的角叫圆心角;
(2)顶点在________,并且两边和圆________的角叫圆周角.
圆心上
圆周上
相交
2.下列各圆中,∠A是圆周角的是( )
A.
B.
C.
D.
A
圆周角定理:一条弧所对的圆周角等于它所对的
圆心角的________.
几何语言:
∵_________________________,
∴________________.
一半
∠ACB和∠AOB都对应
∠ACB= ∠AOB
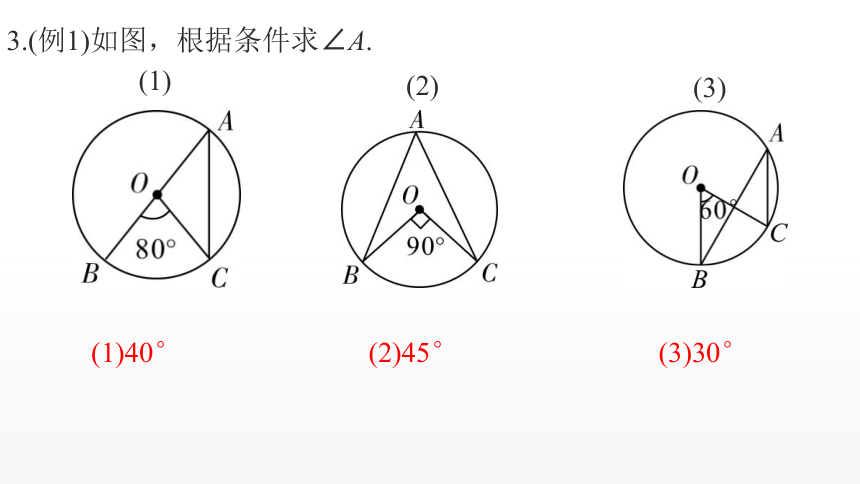
3.(例1)如图,根据条件求∠A.
(1)
(2)
(3)
(1)40°
(2)45°
(3)30°
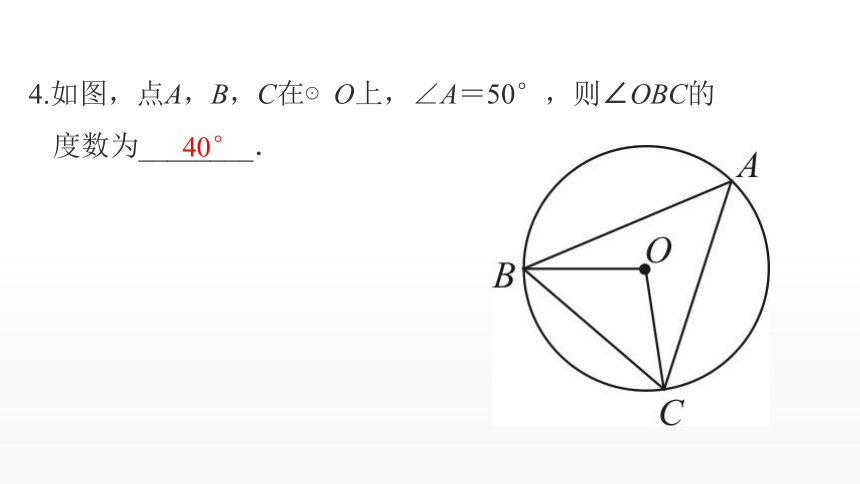
4.如图,点A,B,C在⊙O上,∠A=50°,则∠OBC的
度数为________.
40°
5.如图,点A,B,C在⊙O上,且∠A+∠BOC=120°,则
∠A的度数为________.
40°
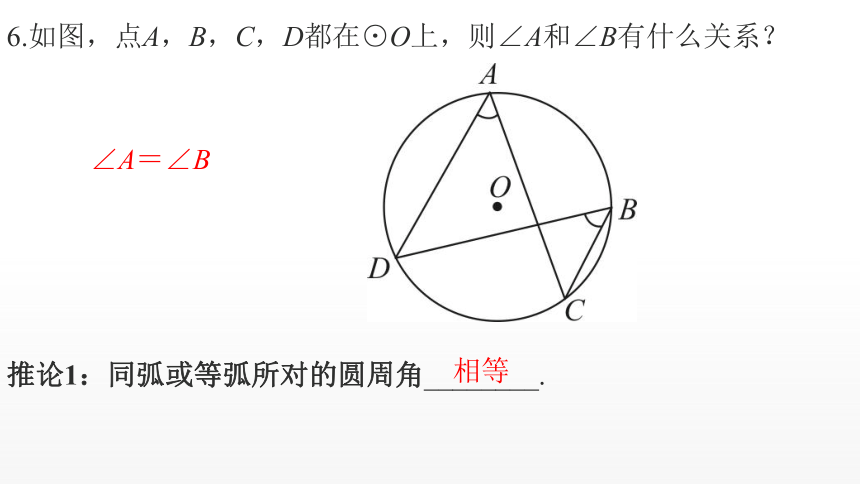
6.如图,点A,B,C,D都在⊙O上,则∠A和∠B有什么关系?
推论1:同弧或等弧所对的圆周角________.
∠A=∠B
相等
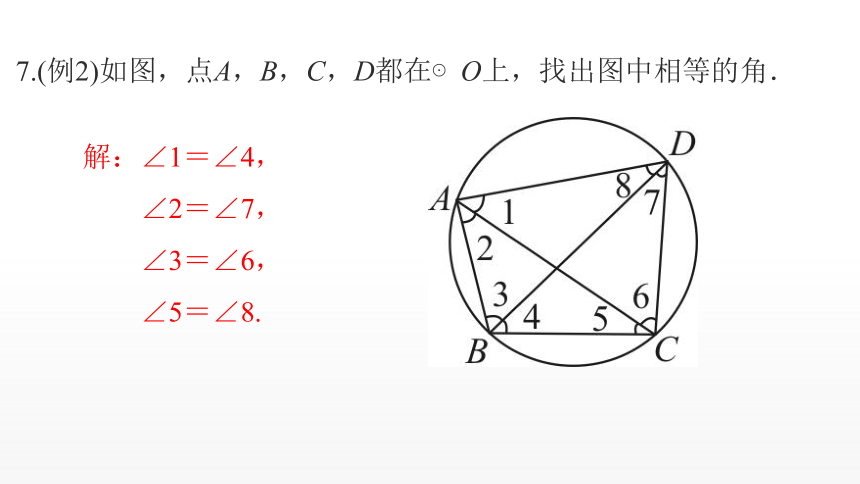
7.(例2)如图,点A,B,C,D都在⊙O上,找出图中相等的角.
解:∠1=∠4,
∠2=∠7,
∠3=∠6,
∠5=∠8.
8.如图,点A,B,C,D,E都在⊙O上, ,
∠D=40°,则∠E=________.
40°
9.如图,点A,B,C,D在⊙O上,则∠A=________,
∠B=________.
∠D
∠C
10.(例3)如图,△ABC是⊙O的内接三角形,P为AB上一点,连
接PC,∠1=∠2=60°.求证:△ABC为等边三角形.
证明:由题意得
∠ABC=∠2=60°
∠BAC=∠1=60°
∴∠ACB=180°-60°-60°
=60°
∴△ABC为等边三角形
11.如图,点A,B,C在⊙O上,点D是 的中点.
求证:∠CAD=∠BCD.
证明:∵点D是BC的中点,
∴
∴∠CAD=∠BCD
(同弧或等弧所对的圆周角相等)
二、过关检测
第1关
12.如图,点A,B,C在⊙O上,∠A=60°,
则∠BOC=________.
120°
13.如图,在⊙O中,OA=2,点B是⊙O上一点,
且∠ABC=45°,则弦AC=________.
第2关
14.如图,A,B,C是⊙O上的三点,∠A=45°,BC=4,
求⊙O的面积.
解:连接OB,OC
∵
∴∠BOC=2∠A=90°
设 OB=OC=x,
则 x2+x2=42 ,解得x=2
∴⊙O面积=(2 )2π=8π
15.如图,在⊙O中,OC⊥AB,∠AOC=60°,求∠D的度数.
解:∵OC⊥AB,
∴ ,
∴∠D= ∠AOC=30°.
第3关
16.如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC .
求证:∠ACB=2∠BAC.
证明:∵∠ACB= ∠AOB,
∠BAC= ∠BOC,
又∵∠AOB=2∠BOC,
∴∠ACB=2∠BAC.
17.如图,四边形ABCD内接于⊙O,点E在对角线AC上,
EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
(1)解:∵BC=DC,∴∠CBD=∠CDB
∵∠BAC=∠BDC,
∠CBD=∠CAD,∠CBD=39°
∴∠BAC=∠CAD=39°
∴∠BAD=78°
(2)证明:∵BC=EC
∴∠1+∠DBC=∠BEC
∵∠BEC=∠2+BAC
由(1)∠BAC=∠CBD
∴∠1=∠2
一、新课学习
1.(1)顶点在________的角叫圆心角;
(2)顶点在________,并且两边和圆________的角叫圆周角.
圆心上
圆周上
相交
2.下列各圆中,∠A是圆周角的是( )
A.
B.
C.
D.
A
圆周角定理:一条弧所对的圆周角等于它所对的
圆心角的________.
几何语言:
∵_________________________,
∴________________.
一半
∠ACB和∠AOB都对应
∠ACB= ∠AOB
3.(例1)如图,根据条件求∠A.
(1)
(2)
(3)
(1)40°
(2)45°
(3)30°
4.如图,点A,B,C在⊙O上,∠A=50°,则∠OBC的
度数为________.
40°
5.如图,点A,B,C在⊙O上,且∠A+∠BOC=120°,则
∠A的度数为________.
40°
6.如图,点A,B,C,D都在⊙O上,则∠A和∠B有什么关系?
推论1:同弧或等弧所对的圆周角________.
∠A=∠B
相等
7.(例2)如图,点A,B,C,D都在⊙O上,找出图中相等的角.
解:∠1=∠4,
∠2=∠7,
∠3=∠6,
∠5=∠8.
8.如图,点A,B,C,D,E都在⊙O上, ,
∠D=40°,则∠E=________.
40°
9.如图,点A,B,C,D在⊙O上,则∠A=________,
∠B=________.
∠D
∠C
10.(例3)如图,△ABC是⊙O的内接三角形,P为AB上一点,连
接PC,∠1=∠2=60°.求证:△ABC为等边三角形.
证明:由题意得
∠ABC=∠2=60°
∠BAC=∠1=60°
∴∠ACB=180°-60°-60°
=60°
∴△ABC为等边三角形
11.如图,点A,B,C在⊙O上,点D是 的中点.
求证:∠CAD=∠BCD.
证明:∵点D是BC的中点,
∴
∴∠CAD=∠BCD
(同弧或等弧所对的圆周角相等)
二、过关检测
第1关
12.如图,点A,B,C在⊙O上,∠A=60°,
则∠BOC=________.
120°
13.如图,在⊙O中,OA=2,点B是⊙O上一点,
且∠ABC=45°,则弦AC=________.
第2关
14.如图,A,B,C是⊙O上的三点,∠A=45°,BC=4,
求⊙O的面积.
解:连接OB,OC
∵
∴∠BOC=2∠A=90°
设 OB=OC=x,
则 x2+x2=42 ,解得x=2
∴⊙O面积=(2 )2π=8π
15.如图,在⊙O中,OC⊥AB,∠AOC=60°,求∠D的度数.
解:∵OC⊥AB,
∴ ,
∴∠D= ∠AOC=30°.
第3关
16.如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC .
求证:∠ACB=2∠BAC.
证明:∵∠ACB= ∠AOB,
∠BAC= ∠BOC,
又∵∠AOB=2∠BOC,
∴∠ACB=2∠BAC.
17.如图,四边形ABCD内接于⊙O,点E在对角线AC上,
EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
(1)解:∵BC=DC,∴∠CBD=∠CDB
∵∠BAC=∠BDC,
∠CBD=∠CAD,∠CBD=39°
∴∠BAC=∠CAD=39°
∴∠BAD=78°
(2)证明:∵BC=EC
∴∠1+∠DBC=∠BEC
∵∠BEC=∠2+BAC
由(1)∠BAC=∠CBD
∴∠1=∠2
