北师大版七年级数学下册1.2 积的乘方 课件(23张)
文档属性
| 名称 | 北师大版七年级数学下册1.2 积的乘方 课件(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 890.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览


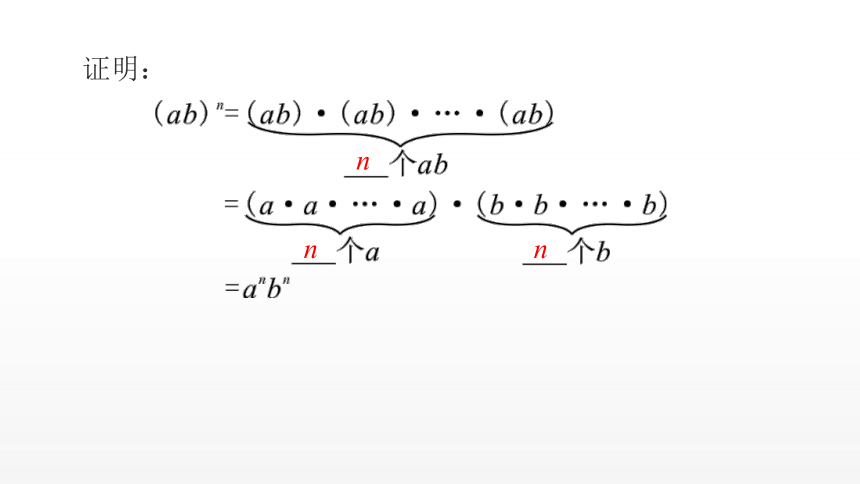

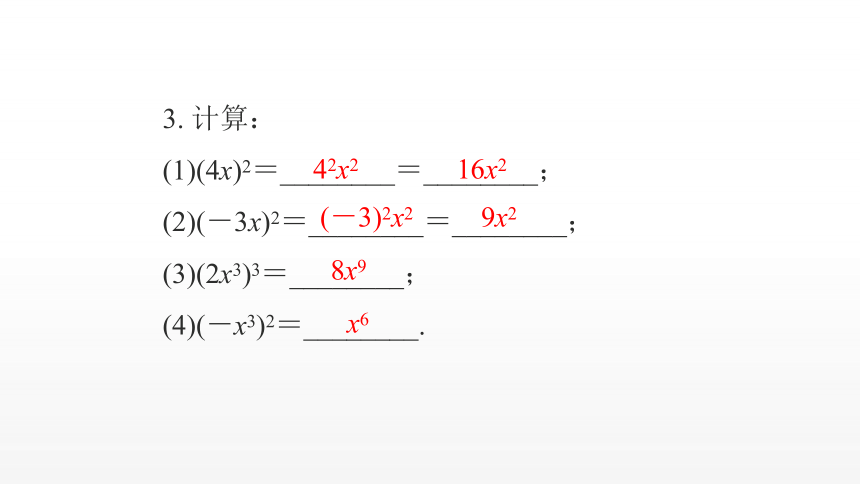

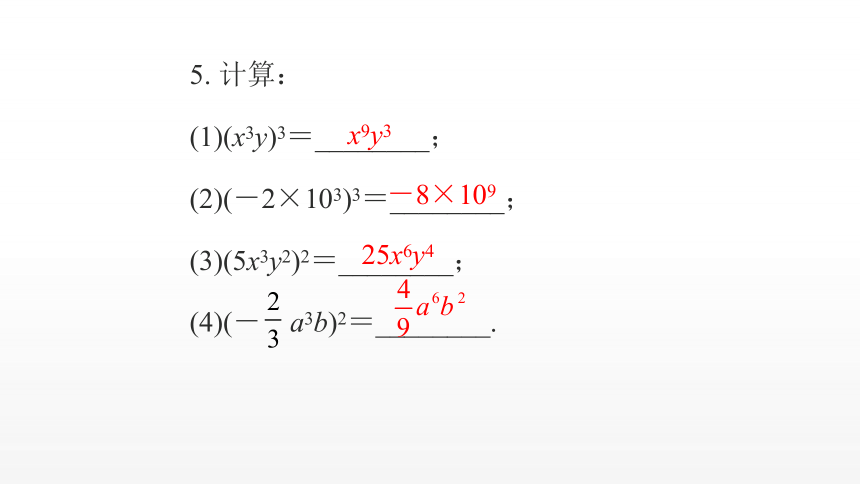


文档简介
第3课 积的乘方
一、新课学习
知识点1:积的乘方
1.计算:22×32=________;(2×3)2=________.
发现22×32________(2×3)2.
积的乘方等于____________________,
即:(ab)n=________(n为正整数).
36
36
=
乘方的积
anbn
证明:
n
n
n
2. (例1)计算:
(1)(3x)2=32·x2=________;
(2)(-2x)3=(-2)3·x3=________;
(3)(5x2)2=__________=________;
(4)(-x2)3=__________=________.
9x2
-8x3
52(x2)2
25x4
(-1)3(x2)3
-x6
3. 计算:
(1)(4x)2=________=________;
(2)(-3x)2=________=________;
(3)(2x3)3=________;
(4)(-x3)2=________.
42x2
16x2
(-3)2x2
9x2
8x9
x6
4. (例2)计算:
(1)(a2b3)2=(a2)2·(b3)2=________;
(2)(3×104)2=________;
(3)(2xy3)3=________;
(4)(- x4y)2=________.
a4b6
9×108
8x3y9
5. 计算:
(1)(x3y)3=________;
(2)(-2×103)3=________;
(3)(5x3y2)2=________;
(4)(- a3b)2=________.
x9y3
-8×109
25x6y4
知识点2:积的乘方的综合运算
6. (例3)计算:
(1)(4x3)2·(- x)3; (2)(-x2)3·(-x3)2.
解:原式=42·(x3)2· x3
=16x6· x3
=-2x9
解:原式=-x6·x6
=-x12
7. 计算:
(1)(3xy3)2·(-x)3; (2)(-x3)4·(-x2).
解:原式=9x2y6·(-x3)
=-9x5y6
解:原式=(-1)4(x3)4·(-x2)
=1·x12·(-x2)
=-x14
知识点3:积的乘方的逆用anbn=(ab)n
8. (例4)计算:
(1)(-2)2 021×
(2)(-2)2 020×
解: 原式=
=(-1)2 021
=-1
解:原式=(-2)2 020×
=
=(-1)2 020×
=1×
=
9. 计算:
(1)0.599×2100;
(2)(-8)2 020×(-0.125)2 021.
解:原式=0.599×299×2=(0.5×2)99×2=199×2=1×2=2
解:原式=(-8)2 020×(-0.125)2 020×(-0.125)
=[(-8)×(-0.125)]2 020×(-0.125)
=12 020×(-0.125)
=-0.125
二、过关检测
第1关
10. 计算(-4x)2的结果是( )
A. -8x2 B. 8x2 C. -16x2 D. 16x2
D
11. 下列计算正确的是( )
A. x2·x3=x6
B. (3x)3=9x3
C. (4a2)2=8a4
D. (ab2)3=a3b6
D
12. 计算:
(1)(3a3)2=____________;
(2)(-2x2)3=____________;
(3)(-a)3=____________;
(4)(-a3)2=____________.
9a6
-8x6
-a3
a6
13. 计算:
(1)(2x2y)3=____________;
(2)(abc)m=____________;
(3)(-5×103)2=____________;
(4) =____________.
8x6y3
ambmcm
2.5×107
第2关
14. 计算:(x2y3)2+x4·(y2)3.
解:原式=x4y6+x4·y6=2x4y6
15. 计算:a·a2·a3+(a3)2-(2a2)3.
解:原式=a6+a6-8a6
=2a6-8a6
=-6a6
16. 若(ambn)3=a9b15,则m、n的值分别为( )
A. 9、5
B. 3、5
C. 5、3
D. 6、12
B
17.若5n=3,4n=2,则20n的值为________.
6
第3关
18. 计算 的结果是( )
A. 1 B. C. D. -1
A
19. 棱长为a×102 mm的正方体的体积为 ,
表面积为 .
6a2×104 mm2
a3×106 mm3
20. 已知x2n=2,求(3x3n)2-4(x2)2n的值.
解:原式=9x6n-4x4n
=9·(x2n)3-4·(x2n)2
=9×23-4×22
=72-16
=56
21. 已知x+y=a,求(x+y)3·(2x+2y)3·(3x+3y)3的值.
解:原式=(x+y)3·8(x+y)3·27(x+y)3
=216(x+y)9
∵x+y=a
∴原式=216a9
一、新课学习
知识点1:积的乘方
1.计算:22×32=________;(2×3)2=________.
发现22×32________(2×3)2.
积的乘方等于____________________,
即:(ab)n=________(n为正整数).
36
36
=
乘方的积
anbn
证明:
n
n
n
2. (例1)计算:
(1)(3x)2=32·x2=________;
(2)(-2x)3=(-2)3·x3=________;
(3)(5x2)2=__________=________;
(4)(-x2)3=__________=________.
9x2
-8x3
52(x2)2
25x4
(-1)3(x2)3
-x6
3. 计算:
(1)(4x)2=________=________;
(2)(-3x)2=________=________;
(3)(2x3)3=________;
(4)(-x3)2=________.
42x2
16x2
(-3)2x2
9x2
8x9
x6
4. (例2)计算:
(1)(a2b3)2=(a2)2·(b3)2=________;
(2)(3×104)2=________;
(3)(2xy3)3=________;
(4)(- x4y)2=________.
a4b6
9×108
8x3y9
5. 计算:
(1)(x3y)3=________;
(2)(-2×103)3=________;
(3)(5x3y2)2=________;
(4)(- a3b)2=________.
x9y3
-8×109
25x6y4
知识点2:积的乘方的综合运算
6. (例3)计算:
(1)(4x3)2·(- x)3; (2)(-x2)3·(-x3)2.
解:原式=42·(x3)2· x3
=16x6· x3
=-2x9
解:原式=-x6·x6
=-x12
7. 计算:
(1)(3xy3)2·(-x)3; (2)(-x3)4·(-x2).
解:原式=9x2y6·(-x3)
=-9x5y6
解:原式=(-1)4(x3)4·(-x2)
=1·x12·(-x2)
=-x14
知识点3:积的乘方的逆用anbn=(ab)n
8. (例4)计算:
(1)(-2)2 021×
(2)(-2)2 020×
解: 原式=
=(-1)2 021
=-1
解:原式=(-2)2 020×
=
=(-1)2 020×
=1×
=
9. 计算:
(1)0.599×2100;
(2)(-8)2 020×(-0.125)2 021.
解:原式=0.599×299×2=(0.5×2)99×2=199×2=1×2=2
解:原式=(-8)2 020×(-0.125)2 020×(-0.125)
=[(-8)×(-0.125)]2 020×(-0.125)
=12 020×(-0.125)
=-0.125
二、过关检测
第1关
10. 计算(-4x)2的结果是( )
A. -8x2 B. 8x2 C. -16x2 D. 16x2
D
11. 下列计算正确的是( )
A. x2·x3=x6
B. (3x)3=9x3
C. (4a2)2=8a4
D. (ab2)3=a3b6
D
12. 计算:
(1)(3a3)2=____________;
(2)(-2x2)3=____________;
(3)(-a)3=____________;
(4)(-a3)2=____________.
9a6
-8x6
-a3
a6
13. 计算:
(1)(2x2y)3=____________;
(2)(abc)m=____________;
(3)(-5×103)2=____________;
(4) =____________.
8x6y3
ambmcm
2.5×107
第2关
14. 计算:(x2y3)2+x4·(y2)3.
解:原式=x4y6+x4·y6=2x4y6
15. 计算:a·a2·a3+(a3)2-(2a2)3.
解:原式=a6+a6-8a6
=2a6-8a6
=-6a6
16. 若(ambn)3=a9b15,则m、n的值分别为( )
A. 9、5
B. 3、5
C. 5、3
D. 6、12
B
17.若5n=3,4n=2,则20n的值为________.
6
第3关
18. 计算 的结果是( )
A. 1 B. C. D. -1
A
19. 棱长为a×102 mm的正方体的体积为 ,
表面积为 .
6a2×104 mm2
a3×106 mm3
20. 已知x2n=2,求(3x3n)2-4(x2)2n的值.
解:原式=9x6n-4x4n
=9·(x2n)3-4·(x2n)2
=9×23-4×22
=72-16
=56
21. 已知x+y=a,求(x+y)3·(2x+2y)3·(3x+3y)3的值.
解:原式=(x+y)3·8(x+y)3·27(x+y)3
=216(x+y)9
∵x+y=a
∴原式=216a9
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
